Relations métriques dans le triangle quelconque

Pré requis:

Le produit scalaire
Aire d’un triangle scalène

ENVIRONNEMENT du dossier:

Index warmaths	Objectif précédent : Aire du triangle quelconque	Objectif suivant : Relations métriques dans le triangle quelconque	Liste des cours sur la trigonométrie.

DOSSIER : le triangle quelconque :

Recherche de la longueur du troisième côté ,lorsque l’on connaît deux longueurs et l’ angle formé par ces deux côtés.

Avec la relation : « »

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

	COURS
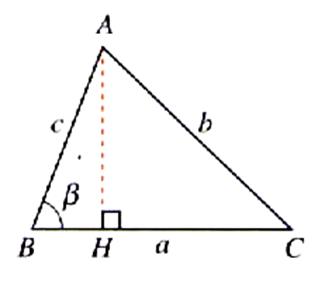
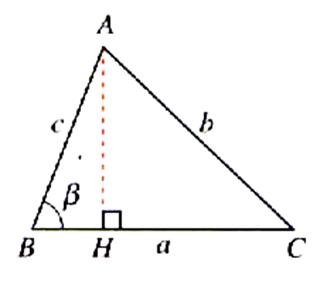
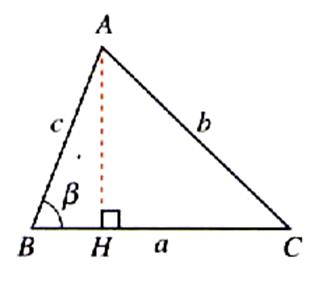
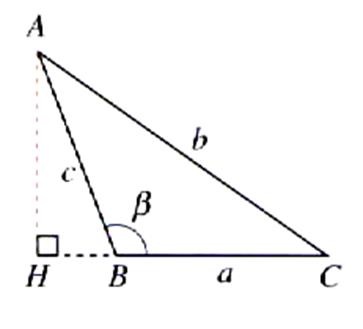
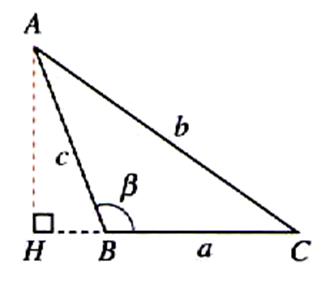
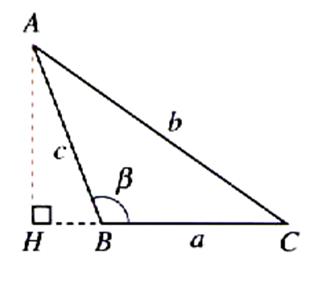
	Figure : cas 1	Figure : cas 2

	Rappel : Aire du triangle :
	Soit le triangle ACB de hauteur AH. Du triangle rectangle AHB nous en déduisons : AH = BA sin b ; ou ; AH = BA sin ( p - b ) ( rappel : sin ( p - b ) = sin b )
	cas 1 : AH = BA sin b L’aire du triangle « S » est égal à : S = BC AH =BC BA sin b	Figure : cas 2 AH = BA sin ( p - b ) = BA sin b L’aire du triangle « S » est égal à : S = BC AH =BC BA sin b

	En posant AC = b ; AB = c ; BC = a ; en « B » = l’angle B ; en « A » l’angle A et en « C » l’angle C . On obtient , par permutation circulaire : S = a c sin B ; S = a b sin C et S = b c sin A

	S = a c sin B = a b sin C = b c sin A
	Théorème : le carré d’un côté d’un triangle est égal à la somme des carrées des deux autres côtés diminuée du double produit de ces côtés par le cosinus de l’ angle formé par ces deux autres côtés.
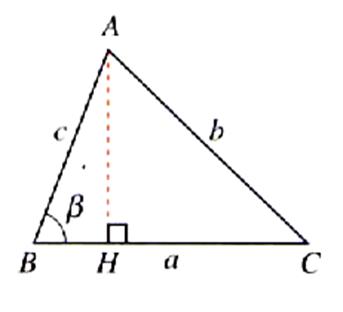
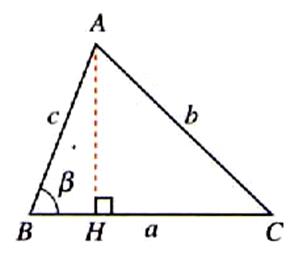
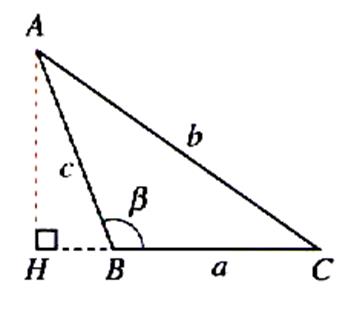
	Figure : cas 1	Figure : cas 2

	Info : calcul de la mesure algébrique…notée exemple :


	En menant la hauteur « AH » du triangle BAC. On a : et Soit : (1) On développe : devient L’égalité ( 1 ) devient : Or :
	Ainsi :
	Calcul de la longueur de BH

	Soit le vecteur de mesure « c » sur l’axe BA à pour projection sur l’ axe le vecteur
	Le cosinus de l’angle des axes BA et est le cosinus de l’angle où B est l’angle en B du triangle ; donc : BH = c . cos
	On peut donc écrire les égalités suivantes : a ² = b ² + c ²- 2 bc cos A b ² = a ² + c ²- 2 ac cos B c ² = b ² + a ²- 2 ba cos C
	Remarques : la seconde et la troisième égalité se déduisent de la première par permutation circulaire. Notez que si l’angle B = un droit (90°) on a le cosinus = 0 et on retrouve la relation de Pythagore .