Caractéristique su Triangle quelconque (scalène)

Index : warmaths

Objectif précédent :

1.     Aire d’un triangle  

Objectif suivant :

1.     Relations trigonométriques dans le triangle quelconque.

2.     Barycentre – vecteurs  et triangle quelconque.

tableau   

Présentation : l’aire et conversions.

Aire des figures élémentaires.

DOSSIER : AIRE d’un Triangle quelconque dont on connaît un angle et la longueur d’un côté .

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité :

Fiche calculs à consulter

Corrigé Contrôle 

Corrigé évaluation 

TRAVAUX :

Niveau relations métriques 

COURS

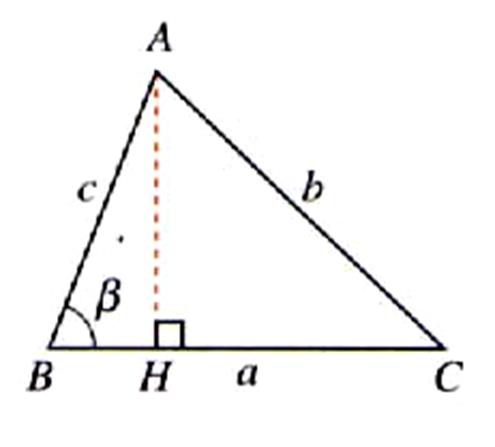
Aire du triangle : cas 1

La hauteur considérée est à l’intérieure de la figure .

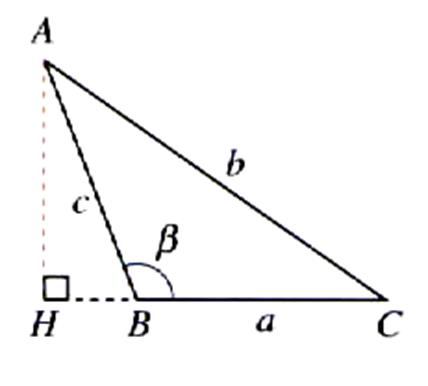
Aire du triangle : cas 2

La hauteur considérée est à l’extérieure de la figure

Aire du triangle quelconque :

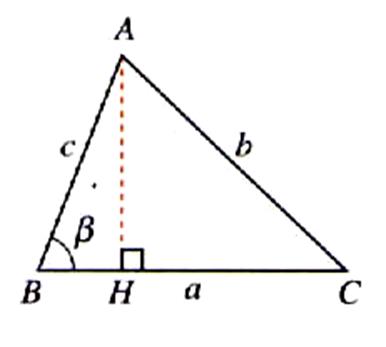
Soit le triangle ACB de hauteur AH.

Du triangle rectangle AHB nous en déduisons :

AH = BA sin b    ;   ou   ;   AH = BA sin ( p - b )  ( rappel : sin ( p - b ) = sin  b  )

cas 1 :

AH = BA sin b

L’aire du triangle « S » est égal à :

S = BC  AH =BC  BA sin b

Figure :  cas 2

AH = BA sin ( p - b ) = BA sin b

L’aire du triangle « S » est égal à :

S = BC  AH =BC  BA sin b

En posant AC = b ; AB = c ; BC = a ; en  « B » = l’angle B ; en « A » l’angle A et en « C » l’angle  C .

On obtient , par permutation circulaire :

S = a  c sin B ;         S = a  b  sin C         et   S = b  c sin A

Conclusion :

 l’aire des triangle quelconques

Est égale :    aux calculs :          S = a  c sin B = a  b  sin C  = b  c sin A

TRAVAUX AUTO FORMATIFS.

CONTROLE:

EVALUATION:

Refaire les exercices ci-dessus ; changer les chiffres des nombres.