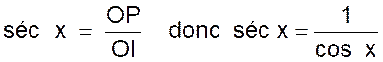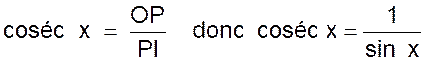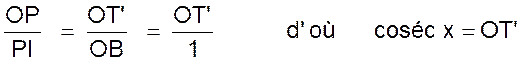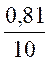|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
Usage des tables des lignes trigonométriques naturelles
dit aussi Usage des tables de rapports trigonométriques . |
||
|
|
||
|
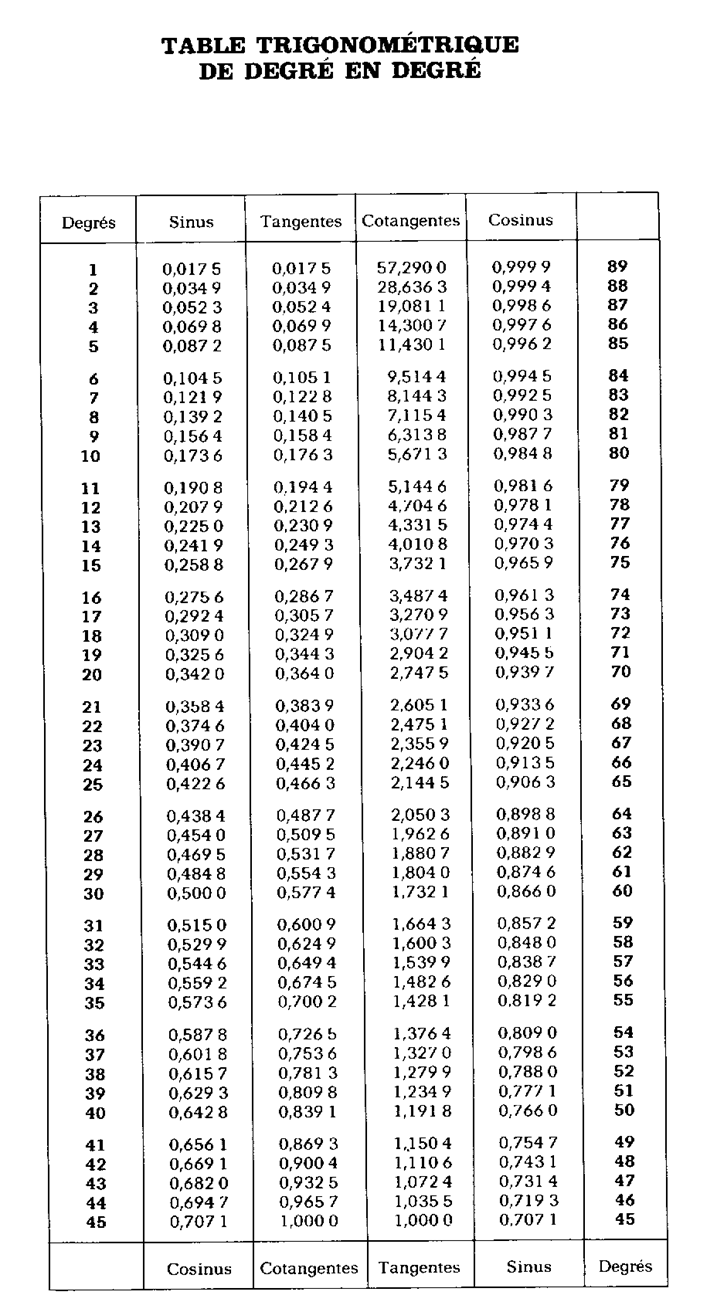
On a calculé la valeur des lignes trigonométriques des angles de 0 à
45° ; les résultats sont consignés dans des tables de deux sortes :
les unes , tables des lignes trigonométriques
naturelles , donnent les valeurs des lignes trigonométriques en nombres
décimaux ; les autres destinées aux calculs très précis, renferment les
logarithmes de ces nombres. Dans la pratique des opérations élémentaires courantes , les tables des lignes naturelles suffisent . Nous mettons à votre disposition
des tables qui permettent de calculer à 4 décimales ( d’autres sont à
3 , ou 5 décimal)les lignes trigonométriques des angles de 0° à
90° , de 10 ,’ en 10’ . Les lignes trigonométriques des angles obtus
s’obtiennent facilement en calculant celles des angles aigus supplémentaires
et en donnant le signe qui convient. Les lectures des sinus , cosinus , tangentes
et cotangentes se font de haut en bas et de gauche à droite avec les
indications du haut de la page pour les angles de 0° à 45°. Ces mêmes
lectures se font de bas en haut et de droite à gauche en tenant compte des
indications de bas de la page pour les angles de 45° à 90° |
||
|
Remarque : les calculatrices scientifiques donne des valeurs à
plus de 10 décimales ! |
||
|
:Vers
la Table N°2 pour plus de
précision ( à
la minute près) |
|
Les tables de rapports trigonométriques fournissent des nombres en
relation avec les angles aigus. Ces tables informent de degrés en degrés ou de grades en grades. Ces tables se lisent de haut en bas pour les angles inférieurs à 45°
ou 50 grades , et de bas en haut pour les angles
supérieurs à 45 ° ou 50 grades. |
|
Leur emploi est immédiat pour les nombres figurant dans la table : Tan 38° = 0,7813
; 0, 8746 = cos 29°
= sin 61° |
|
Si nous ne possédons pas de calculatrice scientifique. Pour les autres valeurs on procède par interpolation en admettant
que : Entre deux valeurs consécutives de la table ,
l’accroissement de l’angle et l’accroissement d’un rapport trigonométrique
sont proportionnels (nous accepterons même si cela n’est pas exacte en vérité) Ces accroissement doivent être pris en valeur
algébrique. |
|
Problème N°1 : Déterminer : sin 32° 25 ‘ et
cos 32° 25 ‘ a) sin 32° 25 ‘ ? On lit dans la table : sin 32° = 0,5299 ; sin 33° = 0,5446 Pour un accroissement de 1° = 60’ ,
l’accroissement du sinus est ( en dix millièmes) : D = 446 - 299 = 147 . Pour un
accroissement de 1’ cet accroissement
serait de ( 147 / 60 ) et pour 25 ‘ la correction
est donc : (147 fois 25) / 60 =
61,25 On arrondit à 61 , ce qui donne , sinus 32° 25 ‘ = 0,5299 + 0,0061 = 0,5360 b )
cos 32° 25 ‘ On opère de même pour le cosinus : seuls différence
, D est négatif ainsi que la correction. On trouvera pour cos 32°
25’ = 0,8442. |
|
Problème N°2 : déterminer a ,
sachant que tan a = 0,7456. |
|
On lit dans la table : 0,7265 = tan 36° et
0,7536 = tan 37° Quand tan a
s’accroît de D = 536 - 265 = 271 , a s’accroît
de 1°
= 60 ‘ Pour un accroissement de 456 - 265 = 191 la correction pour a
sera de ( 60
‘ fois 191) divisé par 271 = 42 ‘ D’où a = 36°42
|
|
Les calculs sont analogues lorsqu ‘ on opère en grades ( il faut remplacer 60 par 10 pour les décigrades ou 100 pour les centigrades). |
|
Compléments
sur les rapports
trigonométriques : sur la « sécante » et la
« cosécante » d’un angle
aigu. |
|
|
Nous pourrions avoir 6
rapports trigonométriques : nous n’en utilisons pratiquement que 3 :le sinus , cosinus et
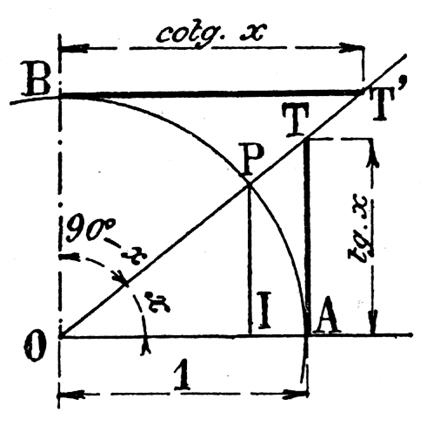
tangente . Soit la
figure ci contre : La sécante d’un angle « x » est le rapport
de l’hypoténuse au côté de l’angle
droit adjacent à « x » et l’on écrit :
la cosécante d’un angle « x » est le rapport
de l’hypoténuse OP au côté de l’angle
droit opposé à « x » d’ où :
|
|
|
Remarque : dans la figure ci dessus on
a :
|
|
|
Et |
|
|
|
|
|
Fin du complément. |
|
|
|
|
|
USAGES DES TABLES. Lignes trigonométriques des angles quelconques. |
|||
|
USAGES
DES TABLES. (SUITE) |
|||
|
Il est nécessaire de savoir utiliser les tables , avant d’utiliser les fonctions de
la calculatrice .Ceci afin de savoir vérifier si on sait utiliser la
calculatrice !!!!!! |
|||
|
|
|||
|
Problème 3 : Trouver la valeur d’une ligne trigonométrique d’un angle
donné : |
|||
|
Sinus : premier cas : l’angle
donné est dans la table. Premier exemple : Soit à trouver sin 36° 20’ On lit immédiatement :
sin 36° 20 ‘ = 0,5925 Cette valeur est en même temps celle du cosinus 53° 40’ ; angle complémentaire de 36°
20’. autres tables (Info table @ ) Deuxième exemple : Premier cas : Soit à trouver sin 56° La lecture des tables donne avec les indications du bas de page :
sin 56° =
sin55° 60’ = 0,829 Deuxième cas : l’angle n’est pas donné dans la
table .Soit à trouver sin 22° 46’ = ? On trouve : sin
22° 40’ = 0,385 et sin 22° 50 ‘ =
0,388 Soit pour 10 ‘ une augmentation de 0,003 appelée différence tabulaire ( DT) Pour une augmentation de 6’ sur l’angle l’augmentation à donner au
sinus sera dons de : ( 0,003 : 10 ) multiplié par 6 soit
= 0,0018 On prendra 0,002 par excès , donc : Sin 22 ° 46 ‘ = 0,385 + 0,002 =
0,387 |
|||
|
Cosinus : à l’inverse du sinus ,
le cosinus croît lorsque l’angle décroît , nous utiliserons cette remarque
dans la recherche du cosinus. |
|||
|
Premier cas : l’angle est donné dans la table . |
|||
|
Exemple : trouver le cosinus de 41° 40’ |
|||
|
Deuxième
cas : si la valeur n’est pas lue directement ,
on calculera la différence tabulaire comme précédemment . !!!!!! |
|||
|
Inversement
on peut à partir d’une valeur d’une ligne trigonométrique ;obtenue ou non par calcul , trouver la valeur de l’angle , en degré
, correspondant. |
|||
|
|
|||
TABLE DE
TRIGONOMETRIE: N°1
|
Exercices :
|
||
|
Le sinus de 36° (0,5878) est
égal au cosinus de 54° |
|||
CORRIGE
|
||||||||
|
Compléter les tableaux suivant :« SINUS
d’un angle » : |
||||||||
|
A )Recherche
du sinus à partir d’un angle |
Avec
la table. |
Avec
la calculatrice scientifique |
||||||
|
1° |
|
|
||||||
|
10° |
|
|
||||||
|
24° |
|
|
||||||
|
30° |
|
|
||||||
|
45° |
|
|
||||||
|
60° |
|
|
||||||
|
90° |
|
|
||||||
|
B )
Recherche d’ un angle à partir d’un nombre
décimal (n £ 1 ) |
Avec
la table. |
Avec
la calculatrice scientifique |
||||||
|
0,2419 |
|
|
||||||
|
0,8290 |
|
|
||||||
|
0,289256198 |
|
|
||||||
|
0,5 |
|
|
||||||
|
0,866 |
|
|
||||||
|
« COSINUS d’un angle » : |
||||||||
|
A )Recherche
du cosinus à partir d’un angle |
Avec
la table. |
Avec
la calculatrice scientifique |
||||||
|
1° |
|
|
||||||
|
10° |
|
|
||||||
|
24° |
|
|
||||||
|
30° |
|
|
||||||
|
45° |
|
|
||||||
|
60° |
|
|
||||||
|
90° |
|
|
||||||
|
B )
Recherche d’ un angle à partir d’un nombre
décimal (n £ 1 ) |
Avec
la table. |
Avec
la calculatrice scientifique |
||||||
|
0,2419 |
|
|
||||||
|
0,8290 |
|
|
||||||
|
0,289256198 |
|
|
||||||
|
0,5 |
|
|
||||||
|
0,866 |
|
|
||||||
|
« Tangente d’un angle » : |
||||||||
|
A )Recherche
d’une tangente à partir d’un angle
|
Avec
la table. |
Avec
la calculatrice scientifique |
||||||
|
1° |
|
|
||||||
|
10° |
|
|
||||||
|
24° |
|
|
||||||
|
30° |
|
|
||||||
|
45° |
|
|
||||||
|
60° |
|
|
||||||
|
90° |
|
|
||||||
|
B) Recherche d’ un angle à partir d’un nombre décimal |
Avec
la table. |
Avec
la calculatrice scientifique |
||||||
|
0,2419 |
|
|
||||||
|
0,8290 |
|
|
||||||
|
0,289256198 |
|
|
||||||
|
0,5 |
|
|
||||||
|
0,866 |
|
|
||||||
|
1 |
|
|
||||||
|
12,56 |
|
|
||||||
|
19 |
|
|
||||||
|
57,2900 |
|
|
||||||
|
169 |
|
|
||||||
|
5067 |
|
|
||||||
|
12568 |
|
|
||||||
|
« cotangente d’un
angle » : |
||||||||
|
A )Recherche
d’une cotangente à partir d’un angle
|
Avec
la table. |
Avec
la calculatrice scientifique |
||||||
|
1° |
|
|
||||||
|
10° |
|
|
||||||
|
24° |
|
|
||||||
|
30° |
|
|
||||||
|
45° |
|
|
||||||
|
60° |
|
|
||||||
|
90° |
|
|
||||||
|
B) Recherche d’ un angle à partir d’un nombre décimal |
Avec
la table. |
Avec
la calculatrice scientifique |
||||||
|
0,2419 |
|
|
||||||
|
0,8290 |
|
|
||||||
|
0,289256198 |
|
|
||||||
|
0,5 |
|
|
||||||
|
0,866 |
|
|
||||||
|
1 |
|
|
||||||
|
12,56 |
|
|
||||||
|
19 |
|
|
||||||
|
57,2900 |
|
|
||||||
|
169 |
|
|
||||||
|
5067 |
|
|
||||||
|
12568 |
|
|
||||||
|
Construction et mesure d’un angle avec une relation trigonométrique
. |
||||||||
|
Construction et mesure d’un angle : |
|
|||||||
|
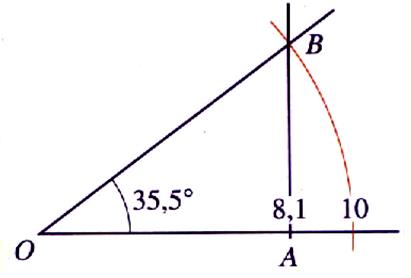
On recherche le cosinus de 35,5° : » 0,81 soit = procédure de tracé : -tracer un arc de rayon 10 cm ; -
sur [ 0x)
placer le point « A » tel que OA = 8,1 cm -
tracer une perpendiculaire à [ 0x) passant par « A » et coupant l’arc de
cercle en « B » -
l’angle AOB vaut 35,5° (à
vérifier avec un rapporteur) |
|
|||||||
|
Conclusion : pour construire un angle on peut
utiliser un rapport trigonométrique. |
||||||||
|
Mesure d’un angle « xOy » donné
sans le rapporteur . |
||||||||
|
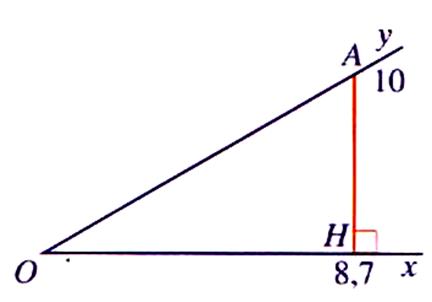
Procédure : -placer un point « A » sur [Oy)
tel que OA = 10 cm ; -
tracer la projection
orthogonale de « A » sur
[Ox)
(image de « A » est « H ») -
mesurer la longueur « OH » ( = 8,7 cm) -
on en déduit le cosinus de l’angle « xOy » = -
A l’aide de la calculatrice ou
de la table : on obtient la valeur de l’angle = 29,5° |
|
|||||||
|
CONTROLE : |
||||||||
|
Citer les 4 rapports trigonométriques. |
||||||||
|
|
||||||||
|
1°) Donner avec la table et la
calculatrice les rapports
trigonométriques des angles suivants : |
||||||||
|
25° = |
31°= |
43°= |
|
57°= |
81°= |
83°= |
|
|
||
|
2°) Déterminer l’angle aigu « x »
tel que : |
||
|
Sin x =
0,48 |
Cos x = 0,1550 |
Tan x = 0,3 |
|
Sin x = 0,84 |
Cos x = 0,9515 |
Tan x = 1,5 |
|
|
||
|
|
||
|
|
||
|
|
||
|
3°) Soit un angle aigu xOy tel que sin xOy = 3/5 a) sans se servir de la table, calculer cos xOy et tan xOy b) construire géométriquement cet angle . |
||
|
|
||
|
Voir les exercices : ci @ info |
||
|
|
||