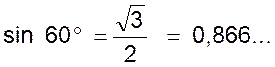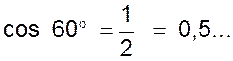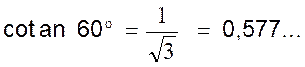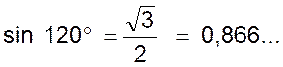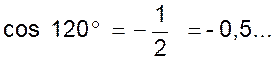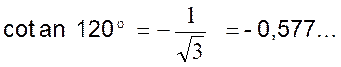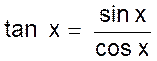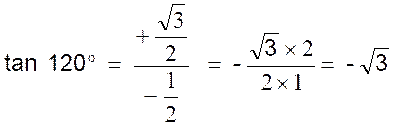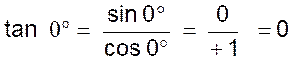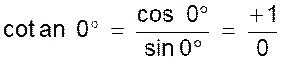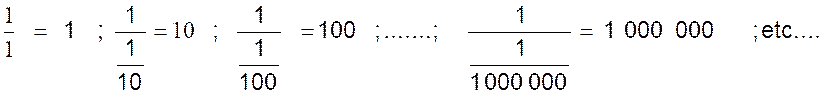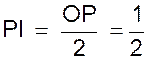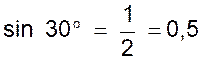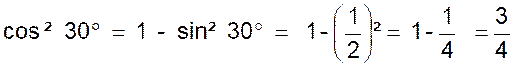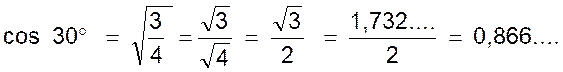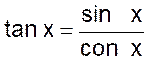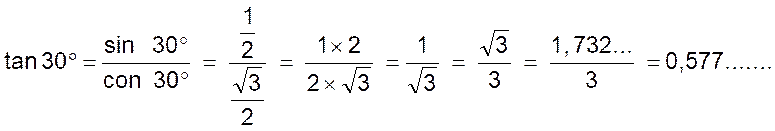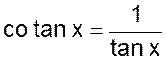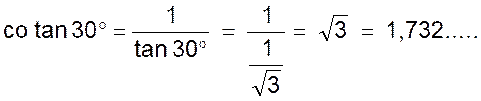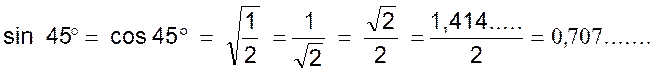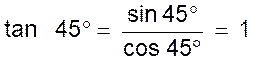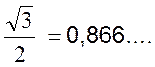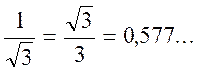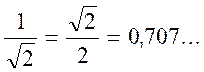Pour Aide et Formation Individualisée

PAGE D ‘ENTREE

ICI pour aller directement aux informations « cours »

INFORMATIONS PEDAGOGIQUES :

DOSSIER : TRIGO

Matière : MATHEMATIQUE

« TRAVAUX »

Leçon : LIGNES TRIGONOMETRIQUES - D’un angle obtus. - D’angles remarquables - D’angles quelconques. - USAGE DES TABLES DE LIGNES TRIGONOMETRIQUES NATURELLES.

Minimum : NIVEAU  V BEP

OBJECTIFS : - connaître les propriétés des lignes trigonométriques

I ) Pré requis: (pour remédiation ou mise à niveau)

Rappel sur les pré requis

Les lignes trigonométriques d’un angle aigu.

II ) ENVIRONNEMENT du dossier :

Index warmaths.

Dossier précédent : 1°) Les notions. 2°) Les lignes trigonométriques d’un angle aigu.

Dossier suivant :

Info : Liste des cours.

III ) INFORMATIONS «  formation leçon » :

Test

COURS

Travaux auto - formation.

Corrigé des travaux auto - formation.

Contrôle

évaluation

INTERDISCIPLINARITE

Corrigé Contrôle

Corrigé évaluation

Chapitres :

1°) Rapports trigonométriques d’un angle obtus

2°) rapports trigonométriques d’angles remarquables. 30° ; 60° , 45° ; 90° ..

3°) Tableau de variation des principaux angles aigus

4°) Usage des tables

IV ) DEVOIRS ( écrits):

Devoir diagnostique L tests.



Devoir Auto - formatif (intégré au cours)



Devoir Formatif « Contrôle : savoir » ; (remédiation)



Devoir Formatif «  Evaluation  savoir faire » (remédiation)



Devoir sommatif.



Devoir certificatif : (remédiation)



* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .

Leçon : LIGNES TRIGONOMETRIQUES - D’un angle obtus. - D’angles remarquables - D’angles quelconques. USAGE DES TABLES DE LIGNES TRIGONOMETRIQUES NATURELLES.

1°) Lignes ( rapports ) trigonométriques d’un angle obtus.

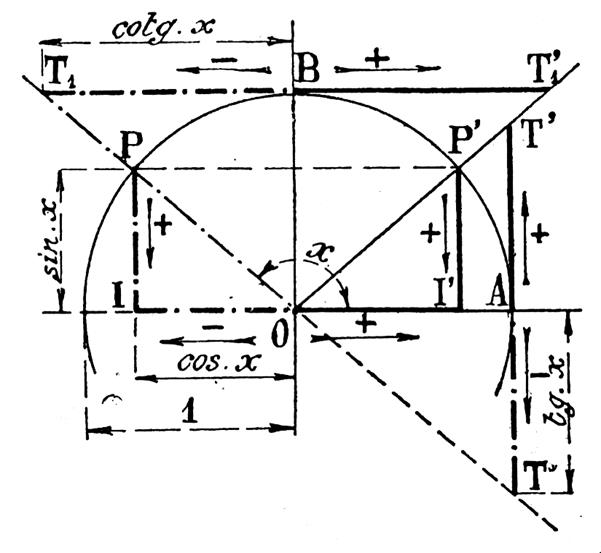
Si au lieu de limiter , comme nous l’avons vu jusqu’à présent , le cercle trigonométrique au premier quadrant , nous considérons une demi - circonférence ou 180° on pourra appliquer à l’angle obtus AOP (figure ci -contre) les constructions et les conventions relatives à l’angle aigu. 1°) Sinus : En abaissant de « P » la perpendiculaire sur le prolongement de AO on obtient en PI le sinus de l’angle AOP = x et l’on écrit sin = PI

2°) Le cosinus de l’angle AOP est encore mesuré par la distance OI comptée du sommet de l’angle au pied du sinus et l’on écrit : cos x = OI 3°) La tangente de l’angle AOP est toujours le segment AT de tangente au cercle mené au point A et limité dans le cas de l’angle obtus au prolongement du 2^ème côté de l’angle. On a donc : tan x = AT 4°) En partant de conventions analogue la cotangente de l’angle obtus est mesurée par BT , et l’on a : cotan x = BT1

A l’étude de la figure ci dessus on constate que : Sur la figure ci dessus : Les lignes trigonométriques de l’angle obtus sont représentées en trait mixte, celle de l’angle aigu en trait continu. Le sens est indiqué par les flèches accompagnées du signe + ou - .

1°) Le sinus de l’angle obtus POA a même valeur et même sens que le sinus de l’angle aigu P’OA supplément de l’angle obtus. . 2°) Les autres lignes trigonométriques de l’angle obtus sont égales mais opposées aux lignes trigonométriques de l’angle aigu qui en est le supplément. On convient en algèbre de distinguer par des signes différents les segments portés dans des sens opposés. On donne le signe + aux lignes trigonométriques de même sens que celles de l’angle aigu et le signe - (moins) aux lignes trigonométriques de sens contraires. Conséquences : 1°) Les lignes trigonométriques d’un angle obtus sont négatives, à l’exception du sinus. 2°) Les lignes trigonométriques de deux angles supplémentaires sont égales en valeur absolue , mais positives pour l’angle aigu et négatives pour l’angle obtus supplément du premier, sauf toutefois pour le sinus qui reste positif. On peut donc écrire les formules générales suivantes : Sin x = sin ( 180° - x ) Cos x = - cos ( 180° - x) tan x = - tan ( 180° - x ) co tan x = - co tan ( 180° - x)

Exemple : nous avons trouvé dans le cours précédent (@ info) que les lignes trigonométriques de l’angle de 60° sont :

On en déduit pour valeurs des lignes trigonométriques de l’angle de 120° supplémenr de 60° :

Remarque 1 : cette propriété explique pourquoi dans l’établissement des tables de lignes trigonométriques on ne donne que les lignes trigonométriques des angles compris : entre 0° et 90° (@ voir tables)

Remarque 2 : les relations fondamentales établies pour les lignes trigonométriques des angles aigus sont applicables aux lignes trigonométriques des angles obtus , à condition de tenir compte des signes. Exemple : la relation (2) appliquée à l’angle de 120° donne :

2°) Lignes trigonométriques de quelques angles remarquables :

A ) Angle nul : 0°

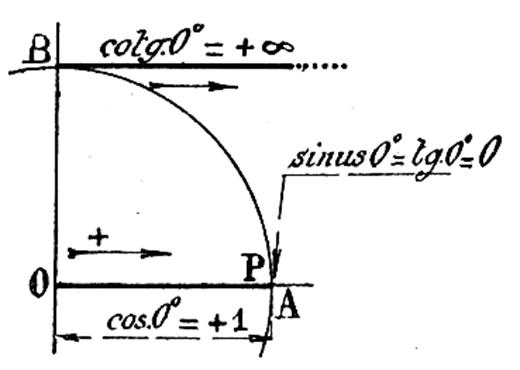
1°) Le sinus de 0° est nul puisque la perpendiculaire abaissé de « P » se réduit au point « P ». On a donc sin 0° = 0 2°) Le cosinus de 0° est égal à OP ou à OA , c’est à dire égal à +1 : cos 0° = +1 3°) La tangente de 0° est nulle comme l’indique la figure ci contre . D’ailleurs

4°) La cotangente de 0° à une valeur absolue infiniment grande . On a en effet en algèbre on apprend que ce quotient est un nombre infiniment grand et l’on écrit : cotan 0° = + ¥

Rappel : si l’on considère en effet les fractions suivantes :

On voit que les dénominateurs successifs : 1 ; (1/10) ; ( 1 / 100 ) ; ………. ; 1 / ( 1 000 000) se rapproche indéfiniment de zéro, ont pour limite « 0 » , et qu’en même temps les quotients grandissent de plus en plus , et n’on pas de limite puisque la suite des nombres est illimitée. Lorsque le dénominateur sera « 0 » , le quotient infiniment gant grand sera représenté par le symbole : ¥ (lire : infini)

La construction géométrique de la cotangente (voir la figure ci dessus) vérifie d’ailleurs ce résulta puisque la cotangente 0° est parallèle à OA.

B) Angles de 30° et de 60°

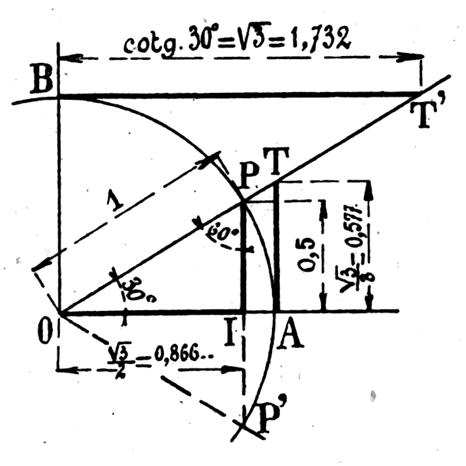
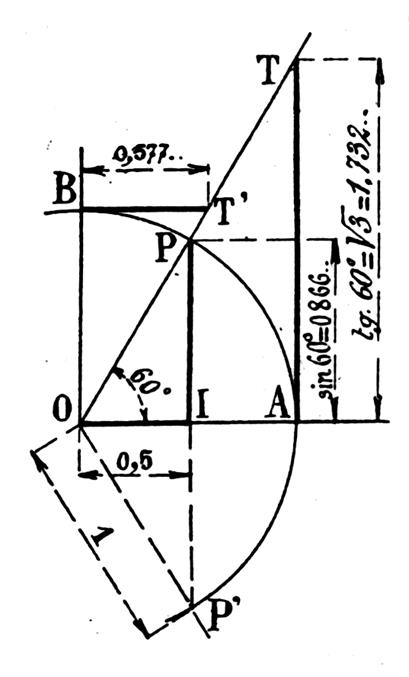
Considérons l’angle POA = 30° Et prenons le symétrique P’ de P par rapport à OA . Le triangle OPP’ est équilatéral et l’on a : donc la relation sin² 30° + cos² 30° = 1, donne successivement :

Et :

La relation donne :

Puisque on a

Les lignes trigonométriques de 30° connues , on en déduit immédiatement celles de l’angle de 60° complément du 1^er .

On a en effet :

cos 30° =

sin 30° =

tan 30° =

cotan 30° =

Ces valeurs ont déjà ailleurs été calculées directement . ( @ info « applications »)

C) Angle 45° :

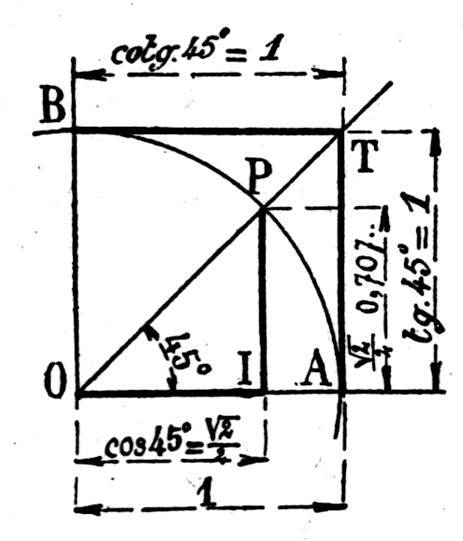
On sait que sin 45° = cos 45° La relation sin² x + cos ²x = 1 donne : sin² 45° + cos ² 45° = 1 D’ou 2 sin² x = 1 donc 2 sin² 45° = 1 Et sin² 45 ° = (1/2)

D’autre part : et

Cotan 45° = tan 45° = 1

D) Angle de 90° : on peut écrire

1°) sin 90° = cos 0° = +1

2°) cos 90° = sin 0° = 0

3°) tan 90° = cotan 0° = + ¥

4°) cotan 90° = tan 0° = 0

Remarques : Les figures dessinées pour les angles remarquables précédents permettent une vérification des valeurs trouvées, par l’utilisation de propriétés étudiées dans le cours de géométrie.

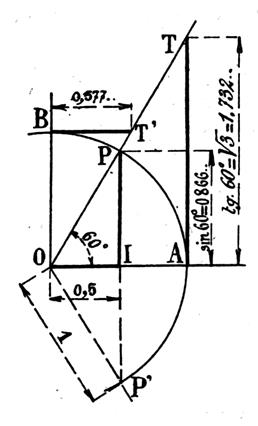
Par exemple, la figure ci contre , utilisée ci dessus , montre que : Cos 60° = 0I = ( OA/2 ) = ( 1/2) Sin 60° = PI = (PP’ / 2) = Tan 60° = AT = 2PI = PP’ =

3°) Les valeurs trouvées précédemment permettent de dresser le tableau suivant qui donne une première idée de la variation des lignes trigonométriques d’un angle aigu :

ANGLES

Sinus

Cosinus

Tangente

cotangente

▼

Augmente de +1 à 0

Diminue de +1 à 0

Augmente de 0 à + ¥

Diminue de + ¥ à 0

0°

0

+1

0

+ ¥

30°

45°

+1

+1

60°

90°

+1

0

+ ¥

0

Remarque 1 : les résultats consignés dans ce tableau indiquent qu’il n’y a pas proportionnalité entre les valeurs des angles et celles de ses lignes trigonométriques : Exemple : sin 60 ° = 0,866… n’est pas le double de sin 30° = 0,5.

Remarque 2 : Si l’on examine ce tableau et que l’on se reporte à ce qui a été dit à propos des lignes trigonométriques de deux angles supplémentaires , on voit que le sinus d’un angle inférieur à 180° est toujours inférieur à +1. et que le cosinus d’un tel angle est compris entre « - 1 » et « +1 » et que la tangente et la cotangente peuvent prendre toutes les valeurs comprises entre « -¥ » et « +¥ »

4 °) USAGES DES TABLES. Lignes trigonométriques des angles quelconques.

A) Usage des tables des lignes trigonométriques naturelles .

On a calculé la valeur des lignes trigonométriques des angles de 0 à 45° ; les résultats sont consignés dans des tables de deux sortes : les unes , tables des lignes trigonométriques naturelles , donnent les valeurs des lignes trigonométriques en nombres décimaux ; les autres destinées aux calculs très précis, renferment les logarithmes de ces nombres. Dans la pratique des opérations élémentaires courantes , les tables des lignes naturelles suffisent . Cette banque de données donne des tables qui permettent de calculer à 3 décimales les lignes trigonométriques des angles de 0° à 90° , de 10 ,’ en 10’ . Les lignes trigonométriques des angles obtus s’obtiennent facilement en calculant celles des angles aigus supplémentaires et en donnant le signe qui convient. Les lectures des sinus , cosinus , tangentes et cotangentes se font de haut en bas et de gauche à droite avec les indications du haut de la page pour les angles de 0° à 45°. Ces mêmes lectures se font de bas en haut et de droite à gauche en tenant compte des indications de bas de la page pour les angles de 45° à 90°

.

B) USAGES DES TABLES.

Il est nécessaire de savoir utiliser les tables , avant d’utiliser les fonctions de la calculatrice .Ceci afin de savoir vérifier si on sait utiliser la calculatrice !!!!!!

Problème 1 : Trouver la valeur d’une ligne trigonométrique d’un angle donné : ( @ info table)

Sinus : premier cas : l’angle donné est dans la table Premier exemple : Soit à trouver sin 36° 20’ On lit immédiatement : sin 36° 20 ‘ = 0,5925 Cette valeur est en même temps celle du cosinus 53° 40’ ; angle complémentaire de 36° 20’. autres tables (Info table @ ) Deuxième exemple : Premier cas : Soit à trouver sin 56° La lecture des tables donne avec les indications du bas de page : sin 56° = sin55° 60’ = 0,829 Deuxième cas : l’angle n’est pas donné dans la table . Soit à trouver sin 22° 46’ = ? On trouve : sin 22° 40’ = 0,385 et sin 22° 50 ‘ = 0,388 Soit pour 10 ‘ une augmentation de 0,003 appelée différence tabulaire ( DT) Pour une augmentation de 6’ sur l’angle l’augmentation à donner au sinus sera dons de : ( 0,003 : 10 ) multiplié par 6 soit = 0,0018 On prendra 0,002 par excès , donc : Sin 22 ° 46 ‘ = 0,385 + 0,002 = 0,387

Cosinus : à l’inverse du sinus , le cosinus croît lorsque l’angle décroît , nous utiliserons cette remarque dans la recherche du cosinus.

Premier cas : l’angle est donné dans la table .

Exemple : trouver le cosinus de 41° 40’ On lit immédiatement cos 41° 40’ = 0,747

Deuxième cas : si la valeur n’est pas lue directement , on calculera la différence tabulaire comme précédemment . !!!!!!

Inversement on peut à partir d’une valeur d’une ligne trigonométrique ;obtenue ou non par calcul , trouver la valeur de l’angle , en degré , correspondant.

CONTROLE :

EVALUATION :

1°) Construire les angles compris entre 0° et 180° admettant pour sinus la valeur 5/7

2°) Construire l’angle ayant pour cosinus ( + 3 / 5 ) et compléter la figure en traçant l’angle ayant pour cosinus ( - 0,6 )

Voir les exercices : ci @ info