Pré requis:

Somme des angles dans un triangle

Nomenclature 1

Le triangle rectangle

ENVIRONNEMENT du dossier:

Index warmaths

Objectif précédent : 1°) Les triangles rectangles semblables ; homothétiques ; .. 2°) Vocabulaire .

Objectif suivant : Les relations trigonométriques dans le T.R. (niv V)

tableau    2°) INFO sur les triangles 3°Les relation trigonométrique dans le triangle rectangle

DOSSIER : LE TRIANGLE RECTANGLE et Les relations trigonométriques :  Vocabulaire.

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

COURS Déjà vu :

Noms donnés  aux angles :

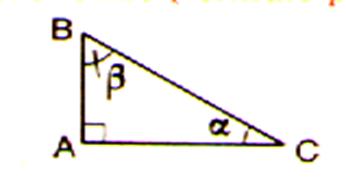
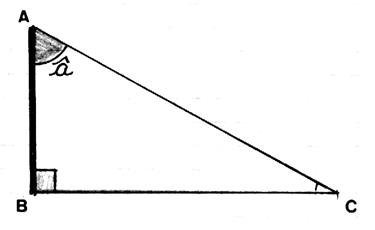
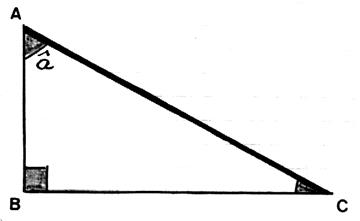
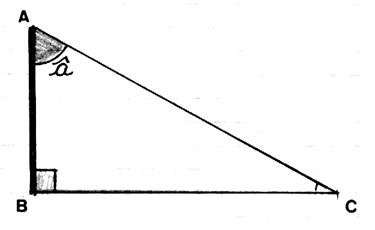
En « A » : un carré (ou rectangle) symbolise l’angle droit.

Pour le symbole « b » lire « bêta » Pour le symbole « a »  lire « alpha »

L’angle  « b » se trouve   à l’opposé  du côté AC.  ( ou CA ) L’angle  « a »  se trouve  à l’opposé du  côté AB  ( ou BA ) Les côté AB et BC sont consécutifs . ( AB est appelé le « côté adjacent » à l’angle « b ») Les côtés AC et CB sont consécutifs. ( AC est appelé le « côté adjacent » à l’angle « a »)

VOCABULAIRE :

 

 

 

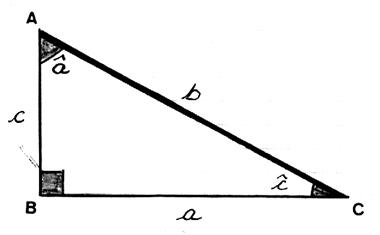
En résumé : si l’on considère l’angle « a » :       dans le triangle désigné par les lettres ABC ,rectangle en B , le coté AC s’appelle « Hypoténuse » le coté AB s’appelle coté adjacent à l’angle « a » le coté BC s’ appelle coté opposé à l’angle « a »

En résumé : si l’on considère l’angle « c » :       dans le triangle désigné par les lettres ABC ,rectangle en B , le coté AC s’appelle « Hypoténuse » le coté BC s’appelle coté adjacent à l’angle « c » le coté AB s’ appelle coté opposé à l’angle « c »

 

Se souvenir qu ’ :

 

Un coté  d’un triangle rectangle  s ’ appelle   ,à la fois,  « coté adjacent  d’un angle »    et « coté opposé » de l’autre angle complémentaire.

                               Un triangle rectangle c’est trois côtés et  5  noms différents. Les cotés formant l’angle droit on deux noms chacun, en fonction ,du choix, de l’angle considéré.

 

ANGLE

Pour former un angle il faut deux coté issus du même sommet :

 

 Un angle droit c’est :  90° = 100gr =  Py  / 2 rad. ( lire pi divisé  2 radians)   (voir les mesures d’un angle)(voir Objectif Angles)

 

SOMME  DES ANGLES.

 

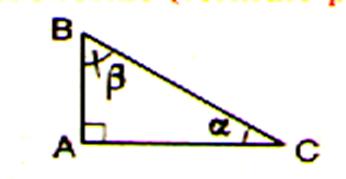
- Somme des angles dans un triangle ( toujours vrai que le triangle soit  rectangle ou non rectangle):

- La somme des angles « b »  et « a »   est égal   90° ; On dit que les angles     « b »  et « a » sont complémentaires .

- Dans un triangle la somme de ses angles est égale à 180°  soit :      

 

Angles complémentaires :

Deux angles sont complémentaires si leur somme est égale à 90° ;

                                                 â + = 90°

(les deux angles qui ne sont pas « angle droit » sont appelés :angles complémentaires)

 

Relation entre  « Angles complémentaires » et « triangle rectangle » :

 

 

Par définition :    Un triangle est rectangle si  deux de ses angles sont complémentaires

                        Les cotés formant  les angles complémentaires ,dans le triangle rectangle, sont appelés : coté adjacent et hypoténuse.

 

 

 

Vocabulaire utilisé dans les  relations trigonométriques.

 

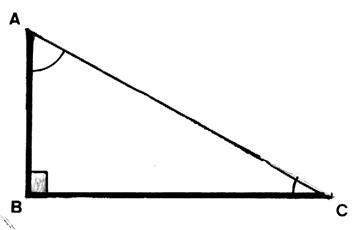
	Le plus grand coté d’un triangle rectangle s’appelle   : HYPOTHENUSE
	Les deux autres cotés  du triangle rectangle forment un angle de 90°   Un coté de l’angle droit et l’hypoténuse forment  un angle dit « aigu ».   Le troisième coté du triangle « empêche » l’ouverture ou la fermeture de l’angle obtenu.
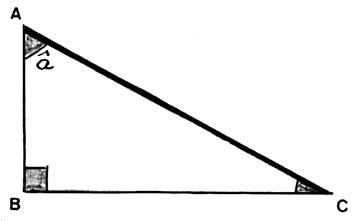
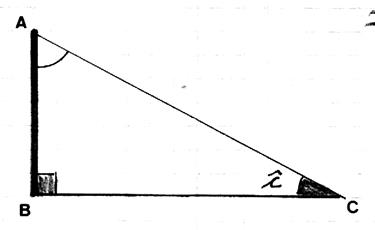
	Que peut-on dire du  coté BC : (par rapport à l’angle â) ? Soit l’angle : â Le coté BC s’appelle « coté opposé » a l’angle â (on peut imaginer que l’on tend une corde de  B à C  pour s’opposer  à l’ouverture de l’angle â )
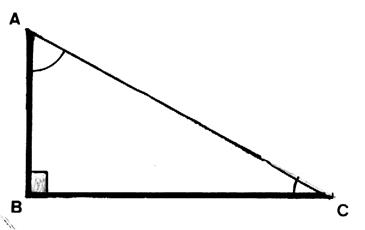
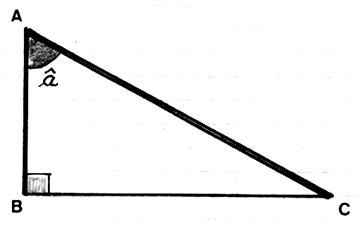
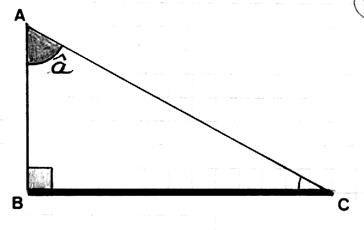
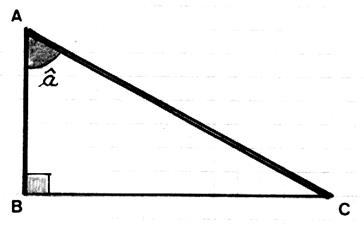
	Soit l’angle : â      ( nous nous plaçons en « A »)       Le coté  AB  s’appelle « coté adjacent » à l’angle â (retenir que le coté adjacent à l’angle et l’hypoténuse forme un  angle , cet angle est dit « complémentaire »)
Pour former un angle il faut deux coté issus du même sommet :                       Dans le triangle rectangle ,les angles  aigus  ( dit aussi  « complémentaires » )   sont formés  par deux cotés appelés :   « coté adjacent » et « hypoténuse ».
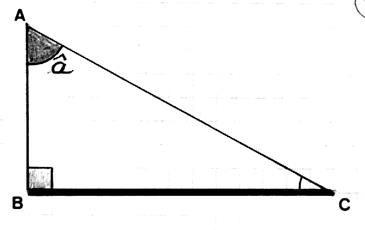
	Application : dans  le triangle rectangle :                  l’angle « a » ,de sommet A ,est formé avec son coté adjacent AB et l’hypoténuse AC
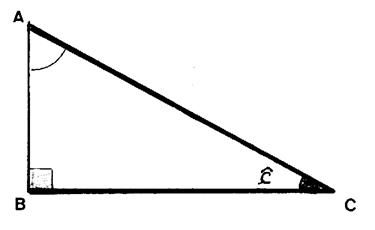
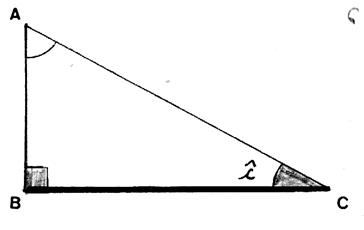
	Application : dans  le triangle rectangle :                l’angle « c » ,de sommet C  ,est formé avec son coté adjacent BC  et l’hypoténuse AC
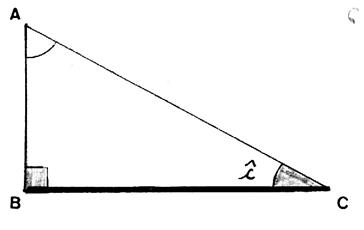
	Considérons l’angle       Soit l’angle    :   le coté BC  s’appelle « coté adjacent » a l’angle         Remarque : le coté BC est  « opposé » à l’angle « a ».
	Considérons l’angle        Soit l’angle        :  le coté AB (ou BA) s’appelle « coté opposé » à l’angle           Remarque : le coté AB  est  « adjacent  » à l’angle « a ».
Se souvenir qu’ :   un coté  d’un triangle rectangle  est  ,à la fois, le  « coté adjacent » d’un angle  et  le   « coté opposé » de l’autre angle complémentaire.  Un triangle rectangle ;  c’est trois cotés et 5  noms différents. Les cotés formant l’angle droit ont deux noms chacun, cela  « en fonction »  , de l’angle considéré.

 

 

 

 

 

 

@ ANGLE : Un angle droit c’est :  90° = 100gr = rad.    (voir les mesures d’un angle)

 

Travaux auto - formatifs.

 

CONTROLE :

 

I )  Compléter les phrases suivantes :

 

a)        Dans un triangle la somme de ses angles est égale à  ..................................

 Donner l’égalité mathématique : ................................

  b )Par définition : un triangle est rectangle si  deux de ses angles sont............................

 

  c ) « deux angles sont complémentaires si leur somme est égale à......... » 

                             Donner l’égalité mathématique :........

 

                        

Que désigne les traits forts  dans les figures suivantes :

..

	Soit l’angle : â
	Soit l’angle : â
	application : dans le triangle rectangle :      on considère   l’angle « a » .............................................................................................................
	Considérons l’angle      .................................................................................................. :
	Considérons l’angle      .................................................................................

 

 

 

:

 

 

 

 

 

 

 

 

 

EVALUATION :

 

      Tracer un triangle rectangle ; placer les lettres   « C » « D » « R »    aux sommets ; nommer  les angles.

Nommer  les cotés par rapport aux  angles : ( coté opposé ou coté adjacent)

 

Dites tout ce que l’on peut dire sur la figure ci contre : Combien de valeurs peut -on mesurer ? Donner ces mesures..

 

APPLICATION :

 

 

 Dans le triangle rectangle ABC:

 

      Considérons l’angle « a » :

       l’angle « a » , de sommet A , est formé avec son coté adjacent AB et l’hypoténuse AC. :

 

                    C’est un angle complémentaire

 

Le coté BC est alors appelé :coté opposé à l’angle « a »

 

 

 

 

 

 

Soit le triangle ABC :

 

Considérons l’angle   :

 

Le coté   BC  s’appelle « coté adjacent » a l’angle 

 

 Le coté   AC étant l’hypoténuse ;

 

l’angle « c » est le deuxième angle complémentaire

 

 

 

 

 

 

 

 

CONTROLE :

 

 

 

I )  Compléter les phrases suivantes :

 

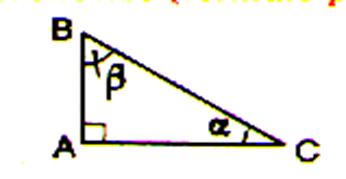
a)   Dans un triangle la somme de ses angles est égale à  …........

b ) Donner l’égalité mathématique : .................................................................

c) Par définition : un triangle est rectangle si  deux de ses angles sont.............................

(deux angles sont complémentaires si leur somme est égale à...................) ;

d ) Donner l’égalité mathématique :.........................................................................

 

II ) Dites ce que désigne les traits forts  dans les figures suivantes :

..

 

  (qu’est ce que AC ? )

 

 

 

......................................................................................

 

 

 

 

 

 

 

Soit l’angle droit  (qu’est ce que AB et BC ? )

..................................................................................................................

 

.................................................................................................................................................................

 

 

 

 

 

 

 

Soit l’angle : â (qu’est ce que BC ? )

................................................................................................................................................................................................................................................................................................................

 

 

 

 

 

 

 

 

 

 

 

Soit l’angle : â (qu’est ce que AB ? )

 

 

.................................................................................................................................................................................................................................................

 

 

 

 

 

 

 application : DANS le triangle rectangle :

     soit  l’angle « a » ;  (qu’est ce que AB et AC ? )

............................................................................................................................................................

 

 

 

 

 

 

 

 

 

 

Considérons l’angle  (qu’est ce que BC ? )

 

 

.................................................................................................................................................................. :

 

 

 

 

 

 

 

 

 

 

 

 

Considérons l’angle    (qu’est ce que AB ? )

 

 

..............................................................................................................................................................