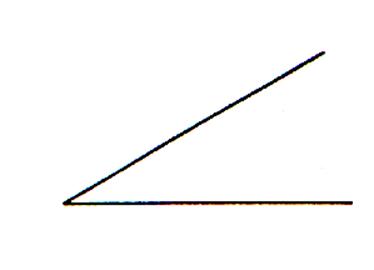Obj : ANGLE et sa MESURE:sommaire

TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité	Corrigé Contrôle	Corrigé évaluation
				Travaux : niv VI et V : Dos. 46 Dos.47

COURS

I ) Définition, mesure et notation :

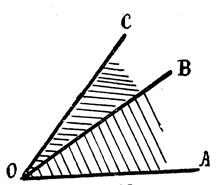
I ) Définition d’un angle et d’un SECTEUR ANGULAIRE

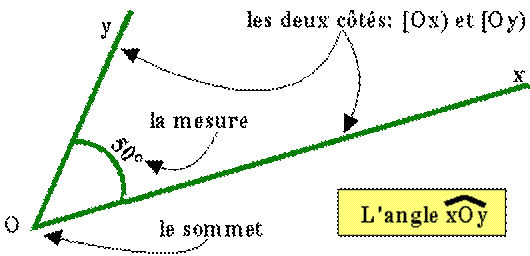
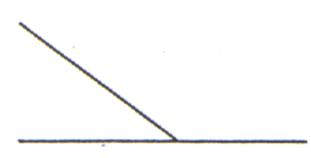
Un angle a un sommet et deux côtés.

La mesure d'un angle ( 50°) ne dépend pas de la longueur de ses côtés. Elle dépend de l'écartement des côtés.

Les unités de mesure sont le degré(°), le grade(gr) et le radian(rd). L'outil de mesure est le rapporteur.

Les deux demi- droites sont issues du point appelé : « sommet »

angle04

Les « secteurs angulaires isométriques » sont des secteurs qui ont la même mesure d’angle .

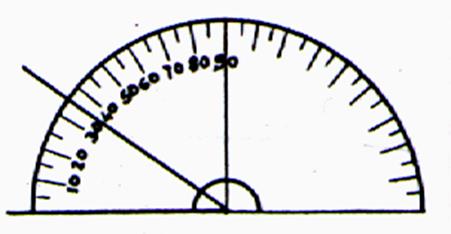
II ) MESURE d ’ UN ANGLE :

L’instrument de mesure d’un angle est un RAPPORTEUR .

( Il est gradué en « degré » ou en « grade » )

On peut connaître la valeur d’un angle par mesure ou par comparaison avec un gabarit d’angle .

Il est possible de comparer un angle avec un instrument de comparaison :

Par exemple : un élève qui possède son matériel de base de géométrie , peut tracer ou peut mesurer par comparaison un angle de 90° ; 45° ; 60° et 30° avec des équerres ( on utilise couramment au collège l’équerre à 45 ou à 60°. )

III ) NOTATION d’un angle :

L ’angle de sommet A est le point de convergence de demi- droites , l’une passe par le point « B » et l’autre demi droite passe par le point « C » , dans ce cas l’angle sera noté : :

Par convention :

La lettre identifiant le sommet « A » se trouve au milieu de deux autres lettres , chacune de ces lettres « B » et « C » représentent deux points appartenant aux demi - droites formant l’angle , la lettre du milieu est surmontée d’un chapeau:

Pour cette écriture « » : lire « angle BAC de sommet « A » , ou « angle CAB de sommet « A »

II ) L’angle : selon sa mesure :

4° ) Angle plat : (info notion)

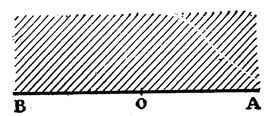
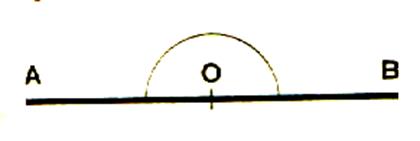
Notion : prendre une feuille Faire un pli .Le repasser.

- Prendre un point O sur ce pli .

- Marquer de part et d’autre du point O le long de la droite , deux lettres A et B

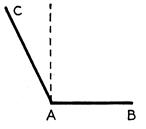
Commentaire : Vous avez un angle ; est un angle qui a ses côtés dans le prolongement l’un de l’autre : c’est un angle plat

O

Représentation graphique

De l’angle plat : un trait et un point « O »

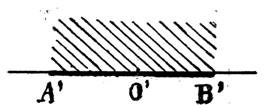
Un angle plat est un angle dont les côtés sont dans le prolongement l’un de l’autre.

On dit aussi que c’est l’angle balayé par la ficelle lorsqu’elle s’arrête après avoir balayé la portion qui correspond à un demi – plan.

an15

Un angle plat a une valeur angulaire de 180 ° ou 200 grades ou p radian.

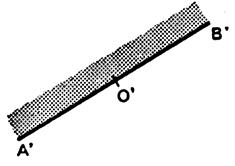
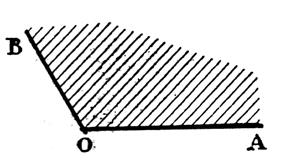
5°) Angle plein

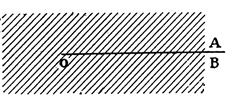
Si les demi – droites O x et O y de même origine O sont confondues , l’angle rentrant qu’elles déterminent recouvre tout plan ; on l’appelle un « angle plein ».

an14

6°) Angle nul

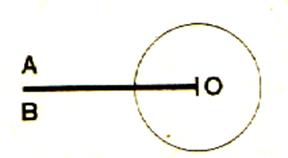
L’autre angle formé par les demi – droites confondues Ox et Oy est un angle saillant ; la portion de plan qu’il occupe est nulle ; on dit que c’est un angle nul .

an13

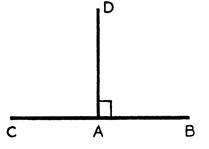
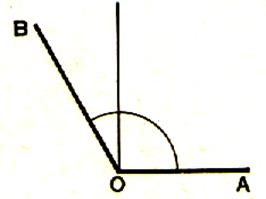
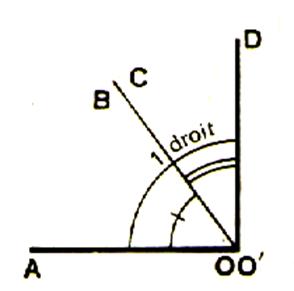
7°) Angle droit

Un angle droit est un angle qui mesure 90°.

Représentation graphique : (deux traits perpendiculaires)

Cet angle est obtenu en traçant une droite perpendiculaire en un point donné à une droite. On dit aussi « qu’en traçant la médiatrice d’un segment on obtient un angle droit ».

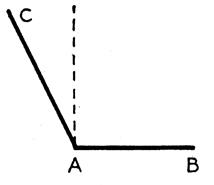
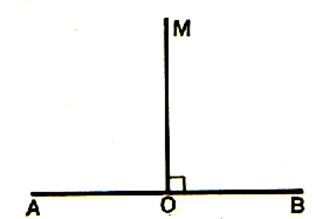
SOS tracé d’un angle droit :droit

Par pliage , nous déterminons la bissectrice OM de l’angle plat AOB . Nous disons que chacun des angles AOM et BOM est un angle droit .

Définition : on appelle “angle droit” un angle égal à la moitié d’un angle plat .

an18

8°) Angle aigu @ :

Angle aigu :

an17

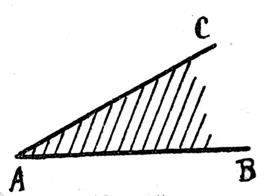
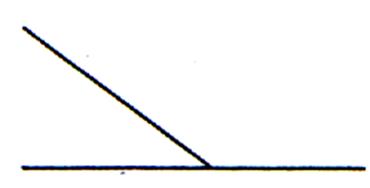
Un angle aigu a moins « d’ouverture » qu’un angle droit (90 ° < ), c’est à dire moins de 90° : ou 100 grades ou p / 2

aigu

IX) Angle obtus

On appelle « angle obtus » un angle saillant supérieur à un angle droit

an16

Un angle obtus est l’angle d’un secteur* obtus : il est supérieur à l’angle droit ( > 90 ° ) , mais inférieur à l’angle plat. ( <180° )

III ) Les angles , selon leurs positions :

10° ) Angles adjacents :

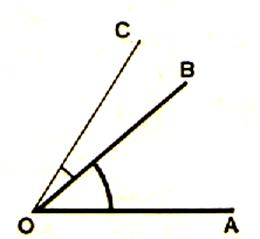
Angles adjacents :

Les angles COB et BOA sont dits « adjacents »

an12

Deux angles adjacents sont deux angles qui :

-Ont un sommet commun

-On un coté commun

-Sont situés de part et d’autre du coté commun.

adjacen

11°) LES ANGLES ASSOCIES :

12°) Angles complémentaires .

(Info +:sur les angles complémentaires dans le triangle rectangle)

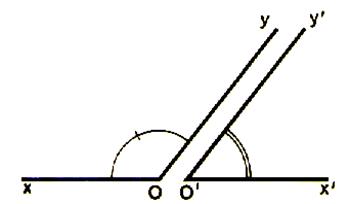
Les angles AOB et CO’D ont pour somme un angle droit .

anCOM2

Ces deux angles sont complémentaires ; nous disons que chacun d’eux est le « complément » de l’autre .

Remarque : si deux angles sont complémentaires , chacun d’eux est inférieur à un angle droit ; ils sont tous deux aigus.

anCOM

Autrement dit :
Deux angles sont complémentaires si leur somme est égale à 90° ; ou un droit .

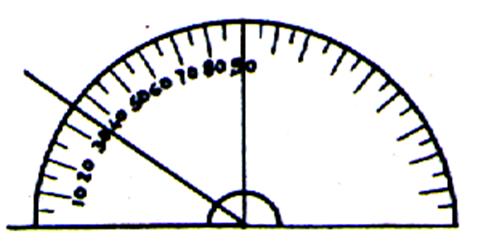
Exemple :La mesure de l’angle se fait avec un rapporteur ( l’angle mesuré est compris entre 0° et 180°)si l’unité choisie est le degré.

Ici l’angle mesuré est de 35 ° ; son complémentaire est de 55 ° et son supplémentaire est de 180-35 = 145° ,

angmesur1

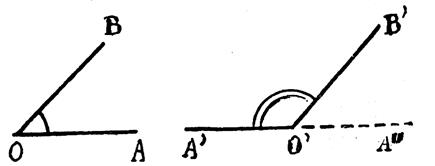
13°) Angles supplémentaires :

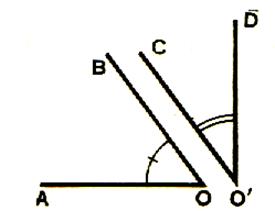
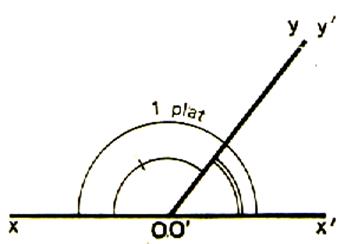
Les angles AOB et CO’D ont pour somme un angle plat .Nous disons que ces angles sont supplémentaires.

ansup

Chacun d’eux est le supplément de l’autre .

auSUP

Autrement dit :

Deux angles sont supplémentaires si leur somme est égale à 180°

supplém

C

A

O

Exemple : On dira que : l’arc BC et l’arc CA sont supplémentaires ; leur somme est égale à l’arc BA.

La mesure de l’arc BC vaut : ..126....°

La mesure de l’arc CA vaut : 54°

la mesure de l’arc AB vaut donc :

126° + 54° = 180°

B

supplém

Autre exemple :

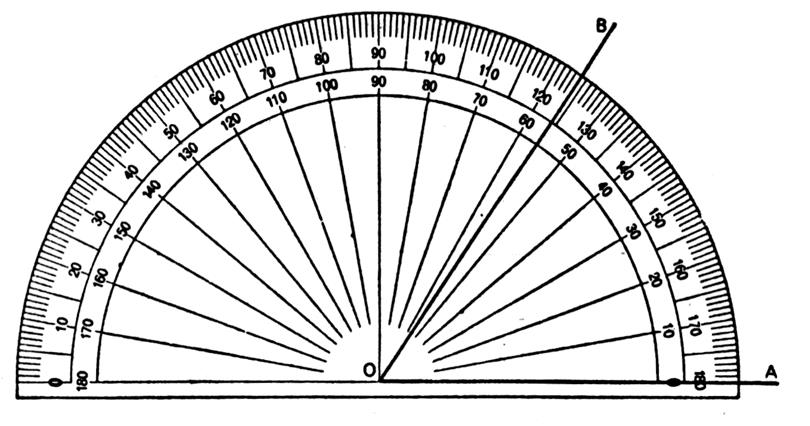
La mesure de l’angle se fait avec un rapporteur ( l’angle mesuré est compris entre 0° et 180°)si l’unité choisie est le degré.

Ici l’angle mesuré est de 35 ° son supplémentaire est de 180 - 35 = 145° ,

angmesur1

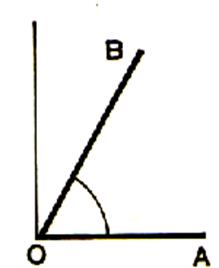
Lire : Angle BOA = 56 °

Remarques :

1°)Les bissectrices de deux angles adjacents supplémentaires sont perpendiculaires

2°)Il en résulte de la définition que si deux angles adjacents sont supplémentaires , leurs côtés extérieurs appartiennent à une même droite .

3°)Si deux angles sont supplémentaires et si l’un est aigu , l’autre est obtus. Si l’un des angles est droit , l’autre est aussi droit .

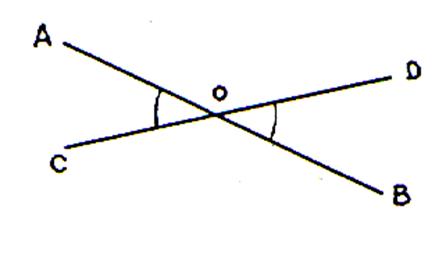
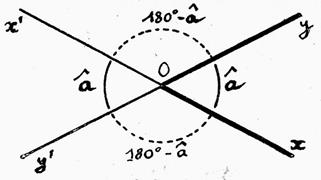
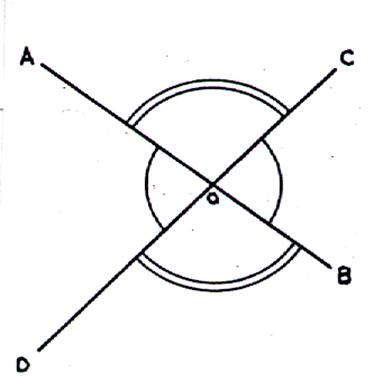
14°) Les angles opposés

Deux angles symétriques par rapport à leur sommet commun sont opposés par le sommet.

Les angles opposés par leur sommet sont égaux.

Hypothèse : AC et DB sont opposés par le sommet ;

Conclusion : AC = DB

Donc :

Hypothèse 1: AC et DB sont opposés par le sommet ;

Conclusion : AC = DB

Hypothèse 2 : AD et BC sont opposés par le sommet ;

Conclusion : AD = BC

secantang2

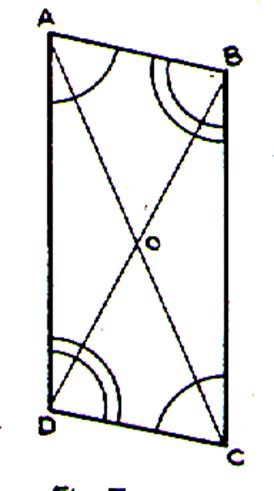
Par extension :

Dans le parallélogramme :

L’angle A et l’angle C sont des angles opposés , ils sont égaux .

L’angle D et l’angle B sont opposés donc , ils sont égaux .

aglpara

15°) Tracés des principaux angles

Voir : les Tracés des principaux angles à 120° ; ...)
Tracés d’autres angles.. ; Et d’autres encore

16°) les angles alternes- internes :

Les angles alternes- internes et les angles alternes externes ( voir deux parallèles et une sécante)

TRAVAUX AUTO FORMATIFS.

CONTROLE

1. Comment appelle t- on l’instrument de mesure d’un angle ? (quel est sa précision ?)

2. Quel nom donne t - on à un angle inférieur à 90° ?

3. Quel donne-t -on à un angle compris entre 90 et 180° ?

4. Quel est la valeur d’un angle plat ?

5. Quelle est la valeur d’un angle droit ?

6. Donner deux façons d’obtenir par le tracé un angle droit.

7. Qu ‘ appelle - t- on « secteur angulaire » ?

8. Qu’est ce qu’un angle aigu ?

9. Qu’est ce qu ’ un angle obtus ?

EVALUATION :

1. Tracer un angle de : 36°

2. Tracer un angle de : 75°

3. Tracer un angle de : 120°

4. Tracer un angle de : 215°

5. Traduire : l ‘ écriture :