Pré requis:
|
|
|
ENVIRONNEMENT du
dossier:
|
Objectif
précédent |
Liste des cours en géométrie plane. tableau |
||
|
|
|
|
|
DOSSIER : Les caractéristiques du
triangle rectangle.
|
|
|
|
|||||
|
|
I
) Première
Caractéristique : demi - rectangle. |
|
|||||
|
|
II ) LES
« 4 »« DROITES et POINTS PARICULIERS . |
|
|||||
|
|
|
||||||
|
|
· 2°) Médiatrices et centre du cercle
circonscrit . |
|
|||||
|
|
· 3°) Les hauteurs et « l’orthocentre » |
|
|||||
|
|
· 4°) Les bissectrices |
|
|||||
|
|
III ) LES ANGLES
dans le triangle rectangle : |
|
|||||
|
|
· Cas particulier : Le demi – carré est un triangle rectangle
isocèle. |
|
|||||
|
TEST |
COURS |
Interdisciplinarité |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
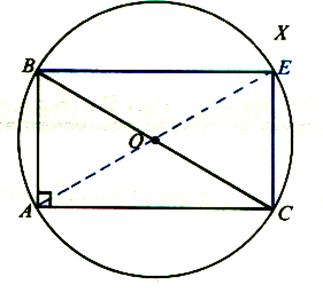
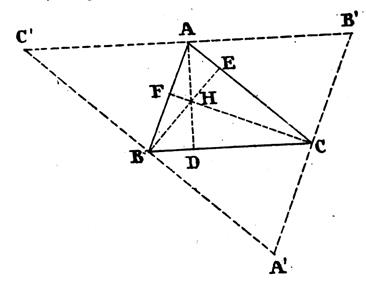
Pré requis : Les diagonales du rectangle sont de
même longueur et se coupent en leur
milieu .
Chaque diagonale est l’
hypoténuse du demi - rectangle
appelé «triangle rectangle »
Le point "O" du rectangle est centre de symétrie .
Les droites xy
et uv , médiatrices des côtés opposés sont axes de symétrie .
*Remarque : Soit le rectangle
BECA ; La figure BCA et la figure
BEC sont des demi - rectangles
. On les appelle " triangle
rectangle" ,
l'un est "rectangle" en A , l'autre
est "rectangle" en E . ( les
diagonales sont appelées : "hypoténuse" )
COURS :
POINT TRES IMPORTANT :Tout triangle rectangle est donc la moitié d’un
rectangle.
|
I
) Première
Caractéristique : |
|
|
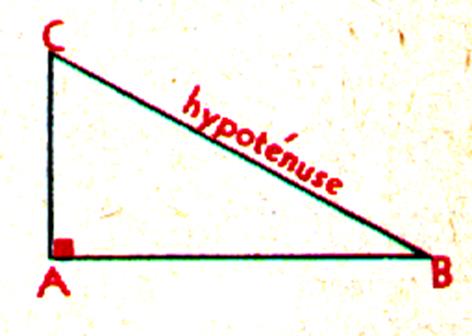
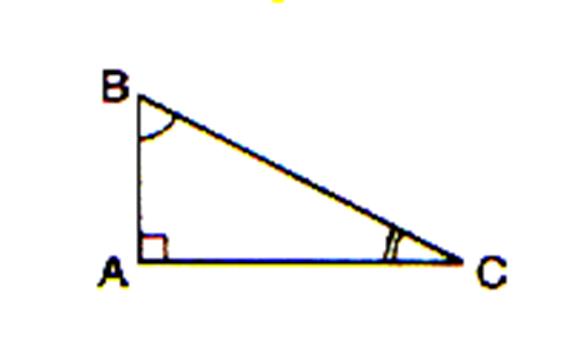
Le triangle rectangle possède un angle droit . Le coté opposé à l’angle
droit s’appelle « hypoténuse » On dit : le triangle ABC rectangle en A , [BC ] est
l’hypoténuse ; Etymologiquement, hypoténuse signifie
« tendu en dessous » ( sous l’angle droit) |
|
|
II ) LES
« 4 »« DROITES et POINTS PARICULIERS : |
|
Pré requis : Les
médianes dans un triangle scalène. |
|
|
Le point d’intersection des médianes est le lieu
du centre de gravité de la figure.
|
|
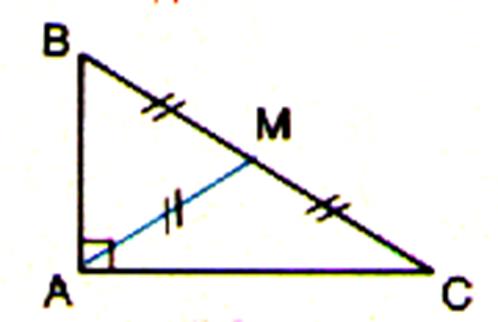
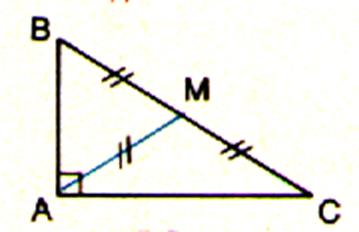
Remarque sur le point « M » ( qui sera appelé aussi centre « O »)
|
Cas particulier :Le point M est à la fois centre
du cercle circonscrit et point de passage de la médiatrice passant par
« A ».le point « A » se trouve donc sur le cercle de
rayon égal à Le
Rayon du cercle =BM =MC =AM
|
|
|
2°)
Médiatrices et centre du cercle
circonscrit . |
|
|
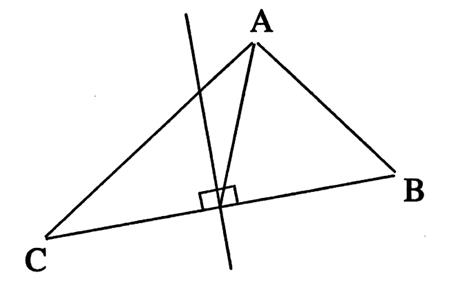
Les médiatrices se coupent en un point
« O ». Le centre du cercle circonscrit se trouve sur le
point O milieu de l’hypoténuse . (« O » lieu du point d’intersection
des médiatrices des cotés )
Ce
point est aussi le point d’intersection
des médianes On dit aussi : que le
triangle est inscrit dans le cercle.
|
|
|
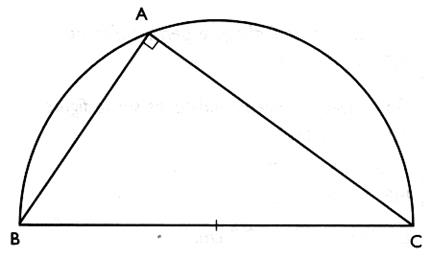
Info plus sur « l’angle inscrit dans un demi-cercle » |
|
|
3°) Les hauteurs et « l’orthocentre » |
|
|
Les deux côtés formant l’angle droit sont des hauteurs. |
Pré requis : Les hauteurs dans un
triangle scalène. |
|
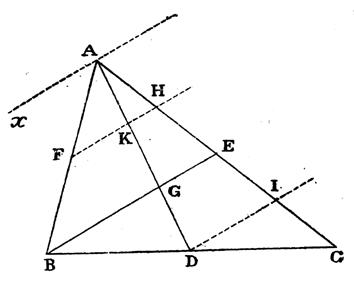
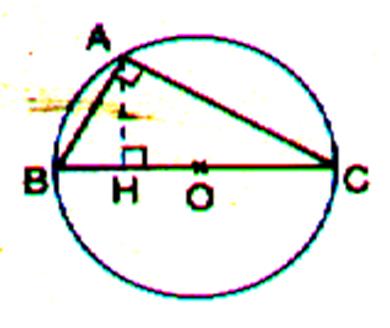
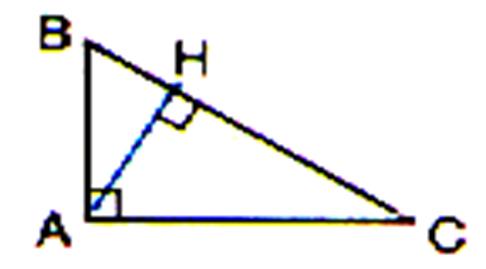
AH est appelé « communément » : la
hauteur du triangle rectangle . L’orthocentre
étant le point d’intersection des hauteurs L’orthocentre du triangle
rectangle se trouve en « A » .(angle droit). Ainsi : un triangle est dit rectangle si deux de ses hauteurs sont confondues avec les cotés
du secteur droit . Voici pourquoi on
parle souvent de la hauteur ( AH )du triangle
rectangle , alors qu’il s’agit de la
hauteur relative à l’hypoténuse. Ci dessous « H » est l’orthocentre du triangle ACB
|
|
|
4°) Les bissectrices |
|
|
les trois bissectrices se coupent en un point : Ce point s '
appelle "centre du cercle inscrit
". (Ce cercle est tangent aux trois cotés) |
|
|
III ) LES ANGLES dans
le triangle rectangle : |
Les
angles
|
|
|
Dans le triangle rectangle la somme des deux angles non droits sont
dits « complémentaires ». *par définition :La
somme de deux angles complémentaires
est égale à 90° . Et la somme
des angles dans le triangle est de 180°. |
|
|
Info + Cd : le triangle rectangle et les
relations trigonométriques
. |
|
|
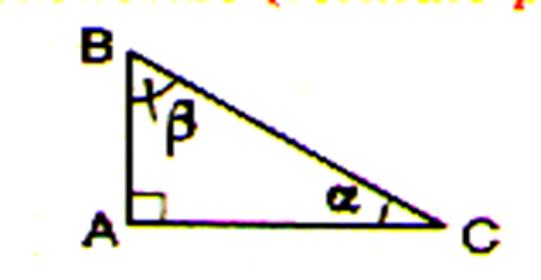
Pour le symbole « b » lire « bêta » Pour le
symbole « a » lire « alpha »
En « A » : un carré (ou rectangle) symbolise l’angle droit. |
|
|
L’angle « b » se
trouve à l’opposé du côté AC.
( ou CA ) L’angle « a » se trouve
à l’opposé du côté AB ( ou BA ) Les côté AB et BC sont consécutifs . ( AB est appelé le « côté adjacent » à l’angle
« b ») Les côtés AC et CB sont consécutifs. ( AC est
appelé le « côté adjacent » à l’angle « a ») |
|
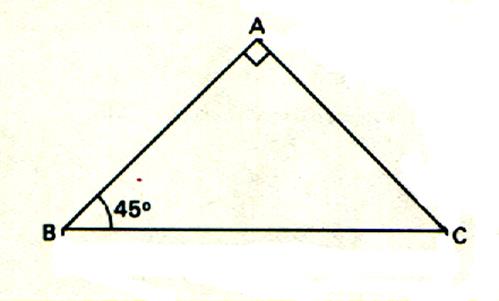
Cas particulier : Le demi – carré est un triangle rectangle isocèle.
|
Un triangle rectangle est isocèle s’il y a deux
côtés isométriques ( à savoir les côtés bordant le
secteur angulaire droit) . Il a alors
deux angles isométriques de 45° ; L’angle B = l’angle C = 45° ; c’est un demi
-carré |
|
TRAVAUX AUTO FORMATIFS.
1°) Compléter la phrase suivante : Tout triangle rectangle est ………………… d’un rectangle.
2°) Quelles sont les caractéristiques principales
d’un triangle rectangle. ?
3°) Que
peut-on dire sur le point particulier
« M . milieu de
l’hypoténuse » ?
(tracer un triangle ABC
rectangle en A)
4°) que peut-on dire des segments de droite BM ; MC ; AM
5°) Quel nom donne-t-on aussi à un triangle
rectangle isocèle ?
1°) Tracer un triangle rectangle.
2°)
Tracer le cercle circonscrit au triangle rectangle dont les côtés de l’angle
droit mesure respectivement