|
Angle |
|
|
Segment |
ENVIRONNEMENT du
dossier:
|
Objectif
précédent: 1°)
"Sommet" |
Objectif suivant 1°) Voir
détermination graphique de la position du centre de gravité du triangle ( 1/3 et 2/3) |
||
|
|
|
|
|
DOSSIER : Les médianes
|
TEST |
COURS |
Interdisciplinarité |
|
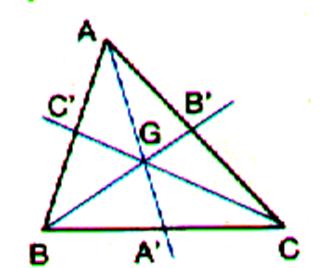
Définition : Une médiane est une droite issue d’un point (sommet d’un angle) et qui joint le
milieu d’un segment.
"MEDIANE" ET
"TRIANGLE" :
Désignation du lieu géométrique du point d'intersection des médianes:
Le point d'intersection des médianes s'appelle le
"centre de gravité" , il est généralement
désigné par la lettre "G"
POSITION du point "G" par rapport aux sommets:
|
Définition : Une médiane est une droite issue d’un point (sommet d’un angle) et qui joint le
milieu d’un segment. Le point "G"
se trouve toujours au 2/3 de la longueur de la médiane en partant de
chaque sommet. (ce qu'il faut démontrer !!!) (ATTENTION : sur la figure ci-contre A', B' et C' ne sont
pas exactement au milieu des segments). |
|
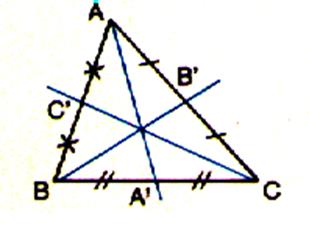
Pour démontrer que G est au 2/3 des sommets ,
il faut tracer 2 parallèles à chaque médiane passant par les milieux de
chaque demi côté.
APPLICATIONS : (lors des calculs en physique,
pour des facilités de calculs, on
"réduit" un "corps" a son centre de gravité,, ainsi pour étudier le déplacement d'un objet on étudie le déplacement de son centre de
gravité.
Avant de savoir déterminer la position d'un centre de gravité d'un volume
( 3 dimensions) il est nécessaire de savoir déterminer
,d'une part , par le graphique et
d'autre part par le calcul ,la position du centre de gravité d'une
surface plane.
Activités :
Voir et savoir déterminer dans la représentation graphique
le centre de gravité des figures
géométrique planes usuelles:
A)
Les polygones usuels sont :
|
Le cercle |
|
|
|
Les triangles |
|
|
|
|
I) Scalènes |
|
|
|
II) Particuliers |
|
|
|
|
Rectangles |
|
|
|
isocèles |
|
|
|
équilatéraux |
|
Les quadrilatères |
I) Polygones quelconques à quatre cotés |
|
|
|
II) Les parallélogrammes : |
|
|
|
|
Le rectangle |
|
|
|
Le carré |
|
|
|
Le losange |
|
|
III) |
Le trapèze |
|
Les autres polygones sont : |
|
|
|
Le pentagone |
(5 cotés) |
|
|
L’hexagone |
(6 cotés) |
|
|
L’ heptagone |
( 7
cotés) |
|
|
L’octogone |
( 8
cotés) |
|
|
L’ennéagone |
( 9
cotés) |
|
|
Le décagone |
( 10
cotés) |
|
B) Cas
des LES POLYGONES REGULIERS :
Un polygone est dit « régulier » lorsque tous ses cotés sont
égaux ainsi que tous ses angles.
Les principaux polygones réguliers sont :
|
Le triangle équilatéral |
|
|
Le carré |
|
|
Le pentagone régulier |
|
|
L’hexagone régulier |
|
|
L ‘ octogone régulier |
|
CONTROLE :
Qu’est qu’une médiane?
TRACER :
Les médianes :
|
Des triangles |
|
Tracer les triangles suivants : |
|
|
I) Scalènes |
1°) Quelconque |
|
|
II) Particuliers |
|
|
|
|
2°) Rectangle |
|
|
|
3°) isocèle |
|
|
|
4°) équilatéral |
|
Triangle quelconque |
|
|
Triangle isocèle: Le dessin est à compléter |
|
|
Triangle rectangle: Le dessin est à compléter; |
|
|
|
|