Lecture :   les POLYGONES

Et  rappel sur les Angles.

Rappel :Il est conseillé de savoir définir et tracer les droites nommées ci dessous., ces connaissances sont utilisées  dans  ce cours !!!!

• Hauteur

• Médiane

• Médiatrice

• Bissectrice 

Index : warmaths

Objectif précédent  

1°) Les triangles :généralités  caractéristiques.

Objectif suivant

1°) Informations sur les triangles.

2°)Cas particulier : le triangle rectangle.

1°)  Résumé « collège »   

2°) Devoir

3°)  Liste des cours disponibles en géométrie plane.

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

1.            Dev.    

2.          vecteurs et homothétie dans un triangle.

Corrigé Contrôle 

Corrigé évaluation 

I )  HAUTEURS:

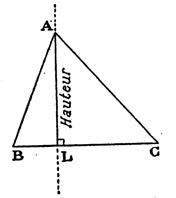
Info  « hauteur »

Définition :on appelle « hauteur » , dans un triangle  , chacune des demi – droites qui , partant d’un sommet , sont perpendiculaires au côté opposé.

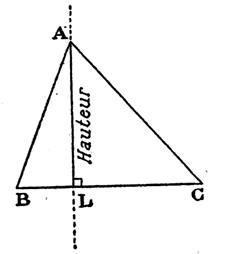
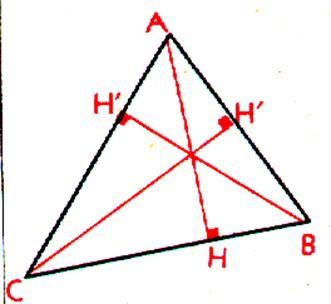
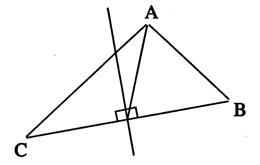
On dit aussi : Les hauteurs sont des  droites perpendiculaires abaissées de chacun des sommets sur les cotés opposés.

Propriété :

Les 3 hauteurs  se coupent ( on dit aussi « concourantes ») en un même point que l'on appelle « orthocentre » du triangle.

On dit aussi que  les 3 hauteurs sont « concourantes ».

Ce point est à l'intérieur du triangle ,lorsque les 3 angles sont aigus.

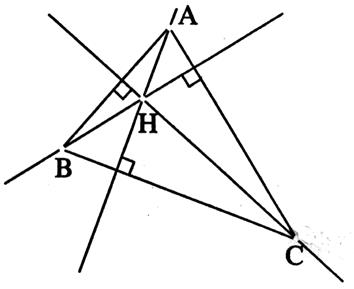
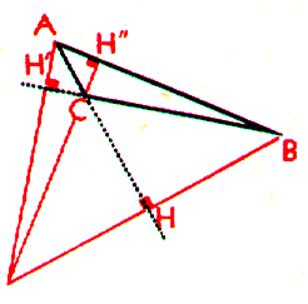
Ce point est à l'extérieur du triangle ,lorsque celui-ci a un angle obtus .

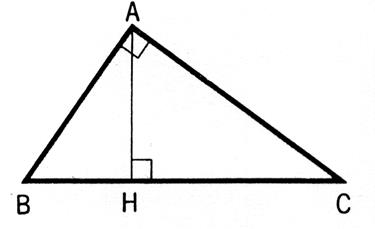
Dans un triangle rectangle , l’orthocentre est au  sommet de l’angle droit.

Le point « A »  est le point d’intersection de hauteurs.

II )  BISSECTRICES

Info « bissectrice »

(pré requis : les bissectrices au collège classe de 6^ème  )

Définition :

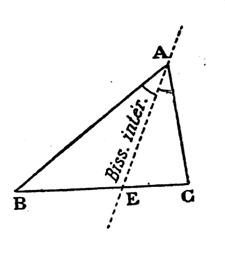
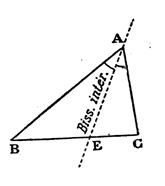
On appelle « bissectrice » , dans un triangle , les  trois demi – droites qui partagent les angles en deux parties égales .

Rappel : la bissectrice intérieure d’un angle est la demi - droite qui partage l’angle en deux angles de même mesure.

Il y a 3 angles dans un triangle , il y a  donc  3 bissectrices.

Ces bissectrices d’un triangle sont les bissectrices intérieures des trois angles.

Ces 3 bissectrices sont concourantes en un point.

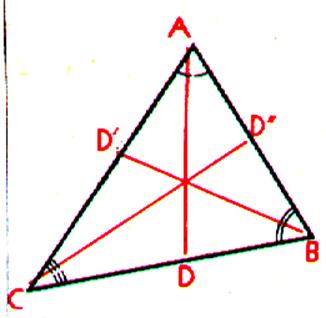
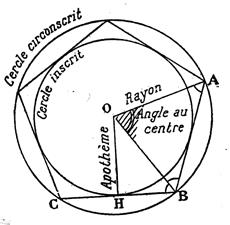
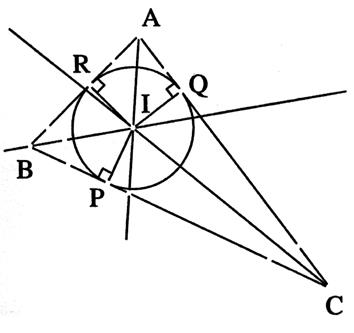
Propriété :les trois bissectrices se coupent en un point ,Le point s' appelle  "centre du cercle inscrit ".

(Ce cercle est tangent aux trois cotés)

Le point « I » est  le centre du cercle inscrit dans le triangle..

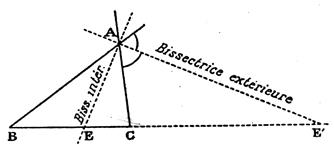
Le rayon du cercle est égal à   IP = I Q = IR

Ci dessous « Info » : sur « bissectrice  intérieure et extérieure - sur cercle inscrit ou circonscrit.

Ci dessous : tracé du cercle inscrit au triangle.

III )  MEDIATRICES

Info « médiatrice »  et  « médiatrice -médiane- hauteur en collège P6 »

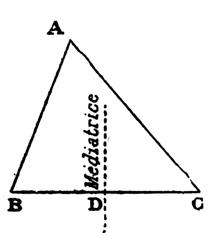
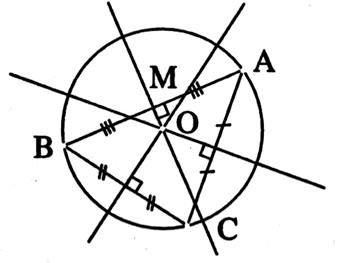
Définition : Les médiatrices d’un triangle sont les médiatrices de ses côtés.

Les médiatrices sont des perpendiculaires élevées au milieu des  3 cotés.

Rappel : la médiatrice « D » du segment AB  (noté :  [AB]) est la droite  perpendiculaire à la droite  notée (AB) qui passe par le milieu du segment AB .

Si  « M » est un point de la médiatrice de [AB] alors  MA = MB.  (le point M est situé à égal distance des points A et B )

Propriété :  Les trois médiatrices sont concourantes en un point qui est le centre du cercle circonscrit.

Circonscrit :se traduit par "écrit autour"

Ainsi : les trois médiatrices d’un triangle ABC sont courantes en un point « O » .Ce point est le centre du cercle circonscrit au triangle.

Le rayon du cercle  est égal à OA  = OB = OC

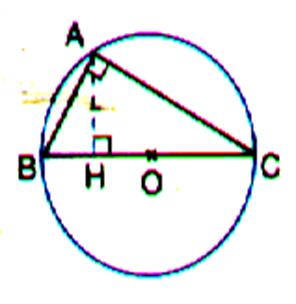
Cas particulier:

Cercle circonscrit dans le triangle rectangle ;le centre du cercle se trouve être le milieu de l’hypoténuse du triangle .

Information :

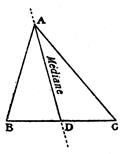
Pour tracer la médiane (issue d’un sommet)  dans un triangle il faut d’abord tracer la médiatrice (du segment)  pour trouver la position du milieu du côté opposé.

Exemple ci contre : on recherche le milieu de CB. ( ce point « milieu »  CB  peut être déterminé après calcul , il est à égale  distance de C et de B .

IV)   MEDIANES

Info « médiane »

La médiane est une droite issue d'un sommet d'un angle est joignant le milieu du coté opposé.

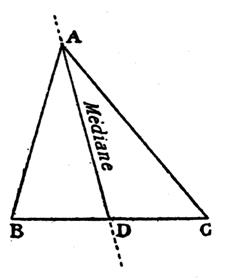
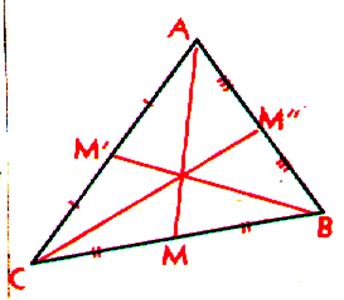
Définition : on appelle « médiane » , dans un triangle , chacun des trois segments qui relient un sommet au milieu du côté opposé.

NB ; le mot « médiane » désigne  aussi la longueur du segment qui est la médiane , et la droite qui la porte .

(Voir CD :symétrie centrale et centre de gravité )

On dit aussi : les médianes d’un triangle sont les droites qui joignent un sommet au milieu du côté opposé.

On dit aussi : que le segment  qui joint le sommet d’un triangle au milieu du côté opposé (à l’angle considéré) est médiane du triangle.

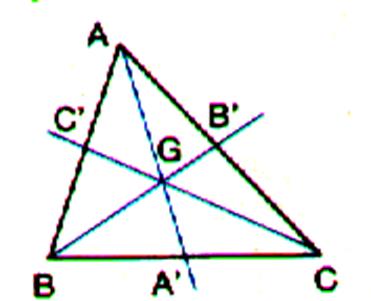
Propriété : « Centre de gravité »

Les 3 médianes  d’un triangle  se coupent en un point G  ( ont dit aussi concourantes) en un point .

Ce point est appelé : centre de gravité du triangle.

Propriété métrique du centre de gravité :

Si A’ , B’ , C’ sont les milieux respectifs de [BC] , [AC],  [AB , on a ]

AG =  AA’ ;  BG= BB’   ; CG =CC’

Le centre de gravité d’un triangle est situé sur chacun des trois médianes à  ( 2 / 3 )  de leur longueur en partant du sommet .

Traité  vectoriel du centre de gravité d’un triangle .

Le centre de gravité ( G) du triangle , qui est le point d’intersection des trois médianes, vérifie l’égalité :

++ =

(voir addition de vecteurs pb. n°5)

On a   =  ;    = ……………………… ( à vous de compléter )

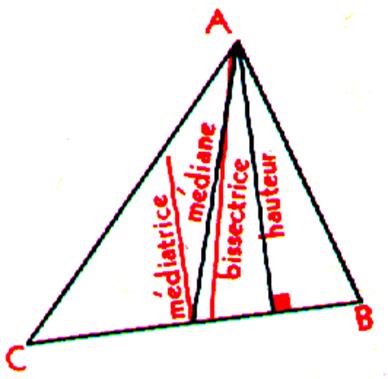
Remarque: Si nous traçons dans un même triangle ,à partir d'un sommet et d'un coté opposé , les droites ci dessus , nous remarquons que ces droites sont distinctes.

Au plus ,dans un triangle il est possible de tracer 4 groupes de 3 droites caractéristiques (soit 12 droites)