CAP industriel._ formation niveau 6 _ 5

Géométrie : DOSSIER : TRACES GEOMETRIQUES/ / Objectif cours 16

Pré requis:

La perpendiculaire vue en primaire.
Les outils de traçage
Les équerres
Le rapporteur
Les angles (tracés)

ENVIRONNEMENT du dossier:

Index warmaths

Objectif précédent 1°)La perpendiculaire 2°)Les médiatrices

Objectif suivant Les tracés de bases 2°) droites et plans perpendiculaires

tableau

DOSSIER :

LES TRACES des PERPENDICULAIRES :

· A l’équerre et la règle ;

· Avec un rapporteur ;

· Avec le compas et la règle ;

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

Remarque : les tracés des perpendiculaires les plus précis se font à la règle et au compas

COURS

Le tracé de perpendiculaires est fondamental , pour tous les corps de métiers

On utilise la règle et le compas ; beaucoup plus souvent l’équerre et quelque fois le rapporteur ( réglable ou gabarit)

1°) Tracé avec l’ équerre et la règle

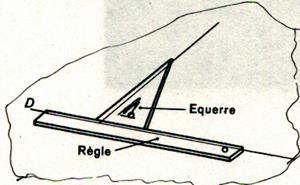
Pour tracer une perpendiculaire à une droite D au moyen de l’équerre
1°) , on appuie cette équerre contre une règle dont un bord suit exactement la ligne droite
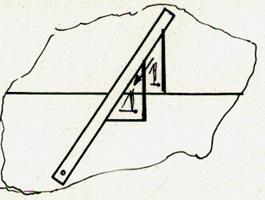
2°) pour augmenter la précision , il est préférable d’utiliser la disposition ci-contre . l’équerre glisse sur la règle. (on dit aussi « translation »)

2 cas de "tracé " d' une perpendiculaire à une droite par rapport en un point donné

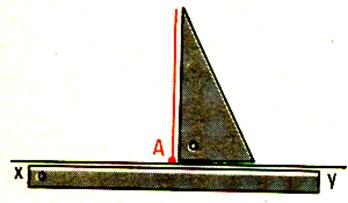
Par le point A , appartenant à xy menons une perpendiculaire	Par le point A pris hors de xy menons une perpendiculaire à xy

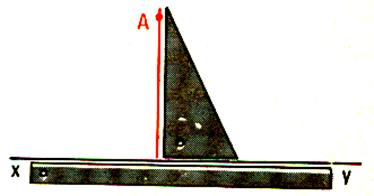
Activité : A l’aide de l’équerre ; reconnaître dans les dessins suivants les lignes perpendiculaires : (entourer le numéro des dessins dont les lignes sont perpendiculaires.

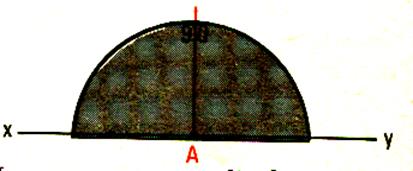
2° Tracé d’une perpendiculaire avec un rapporteur

Placer le point O du rapporteur en A , Aligner xy avec le 0° - 180° ; Placer un point sur la graduation 90° Avec une règle tracer la droite passant par A et « 90° »

3 °) Tracé avec la règle et le compas :

1°) Elever une perpendiculaire sur le milieu d’une droite
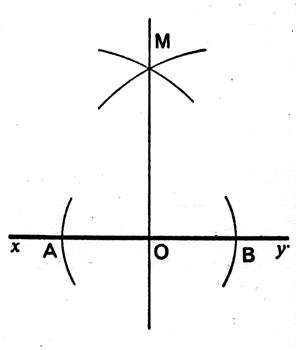
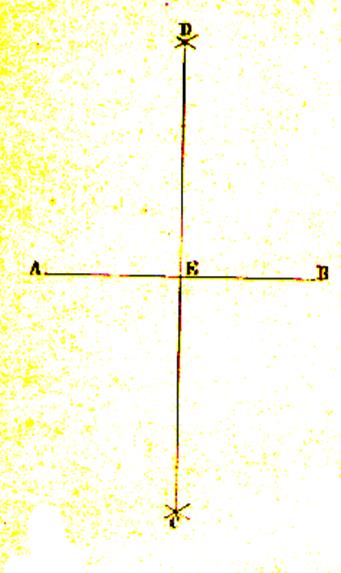
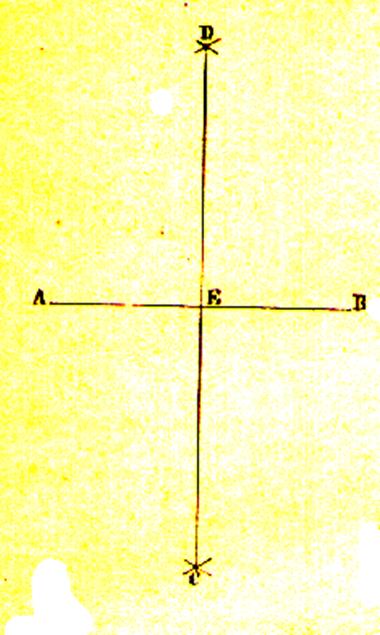
Soit une droite AB donnée ; des points A et B ; comme centre de cercle ,avec une ouverture de compas plus grande que la moitié de AB ,on décrit deux arcs de cercle qui se coupent en C et D ; on joint ces deux points par une droite ; cette droite est perpendiculaire à la ligne AB , et , de plus elle la partage en deux parties égales au point E. Voir « médiatrice d’un segment »

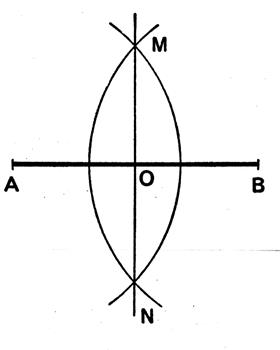
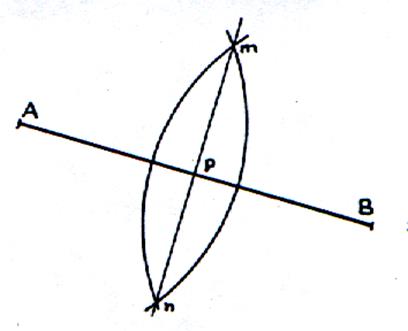
Partager un segment de droite AB en deux parties égales .	INFO sur :Les cercles « positions »
Tracer de A et de B deux cercles sécants de même rayon et choisi assez grand pour que les cercles se coupent en « m » et « n » . Joindre les points « m » et « n » . Le point P est le milieu de AB et mn est l’axe de symétrie du segment AB.

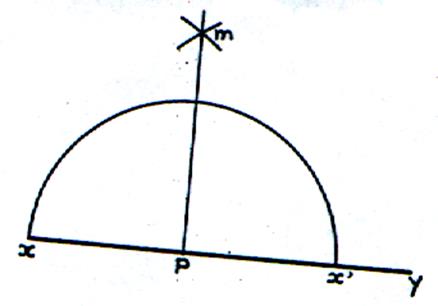
2°) Elever une perpendiculaire à une droite par un point donné sur cette droite.
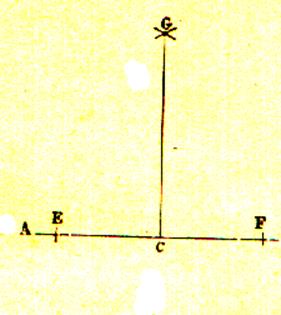
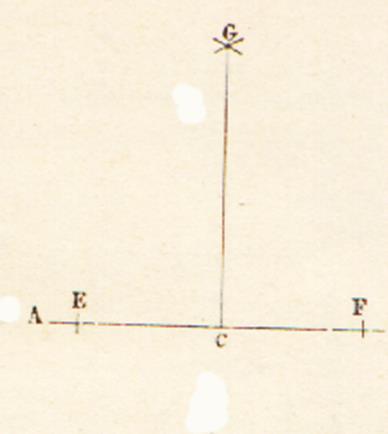
Soit une droite A à laquelle il faut élever une perpendiculaire au point C : A droite et à gauche de ce point C on prend deux distances égales (avec une même ouverture de compas) CE et CF ; ensuite , des points E et F , comme centres , avec une ouverture de compas assez grande , on détermine un point d’intersection G , et on tire la droite GC qui est perpendiculaire à la droite A.

Le point « P » se trouve sur x x ’ : Tracer un arc de cercle interceptant « y » en « x » et « x’ ». Tracer de x et de x’ deux arcs de cercles de même rayon , sécants en « m » ; joindre « m P » La droite est la médiatrice du segment xx’

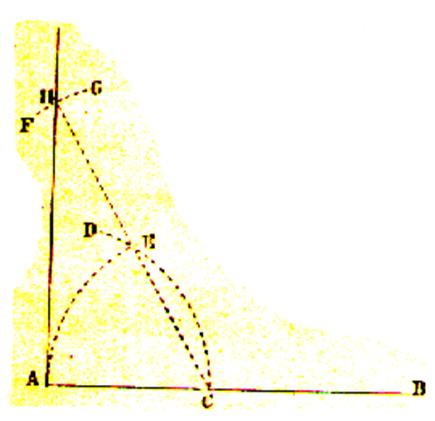
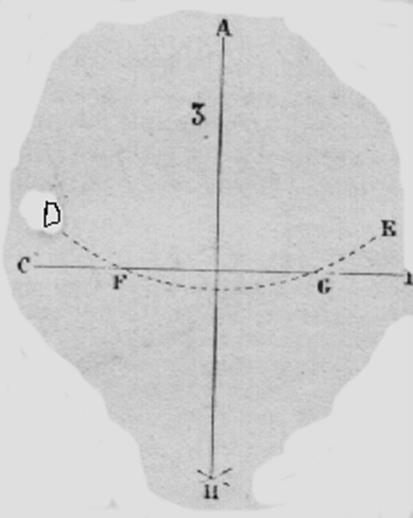
3 ° ) Par un point A , pris hors d’une droite CB , abaisser une perpendiculaire à cette droite.
Du point A , comme centre , avec un rayon suffisamment grand , on décrit un arc de cercle DE , qui coupe la CB aux points F et G ; de ces derniers points , comme centre ,on détermine un point d’intersection H , et l’on tire la droite AH , qui est perpendiculaire à CB. Voir « hauteur dans un triangle »

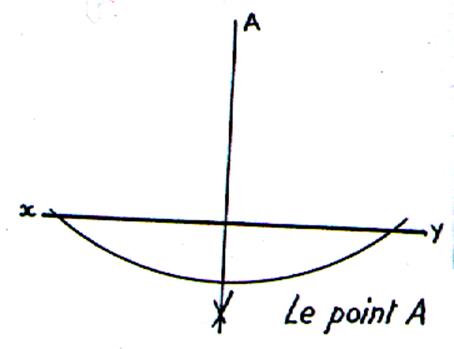
C Le point A est hors de la droite x y : Tracer de A un arc de cercle qui coupe la droite en « x » et « y » . De « x » et de « y » , avec un même rayon , choisi assez grand pour que les cercles se coupent , décrire deux arcs de cercles qui se coupent en un point « C »

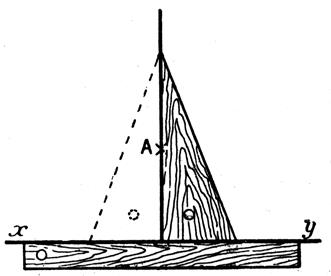
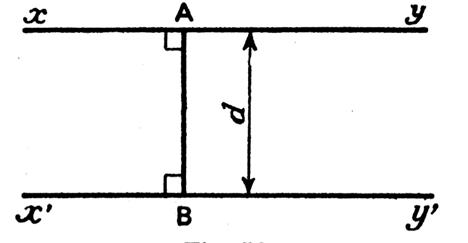
Pour déterminer sur les bords d’une plaque de métal ou de bois , etc…ou d’une feuille de dessin deux droites perpendiculaires ; qui serviront de guide pour tous les autres tracés , on est conduit à résoudre le problème suivant :

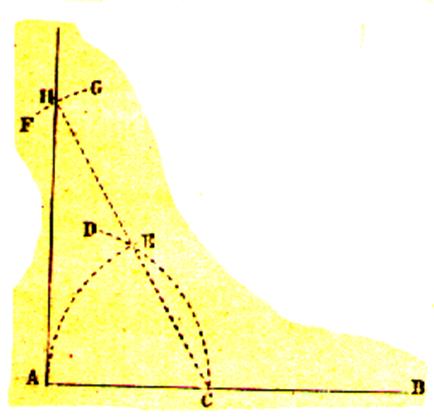
4°) Elever une perpendiculaire à l’extrémité A d’une droite AB , qu’on ne peut prolonger

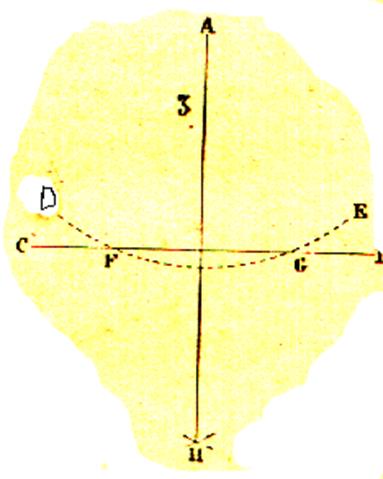
Du point A , comme centre , avec une ouverture de compas arbitraire , on décrit un arc indéfini CD ; du point C , avec le même rayon ,on détermine le point d’intersection E ; de ce dernier , comme centre , toujours avec le même rayon , on décrit l’arc indéfini FG ; puis on tire une droite passant par les points C et E , et on prolonge jusqu’à la rencontre de l’arc FG , ce qui donne le point H , on mène la droite HA , qui est la perpendiculaire demandée.

INFO plus
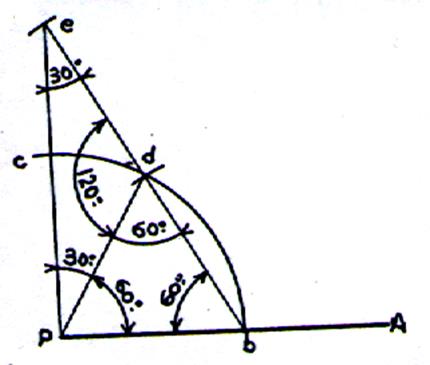
Observé : e db est l ‘hypoténuse du triangle rectangle . ed = db = dp tracer le triangle équilatéral « p d b » prolonger « d b » ; placer « e » joindre joindre

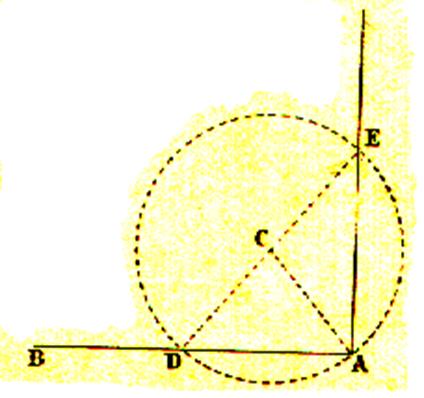
5°) Elever , par un autre moyen , une perpendiculaire à l’extrémité d’une droite qu’on ne peut prolonger.
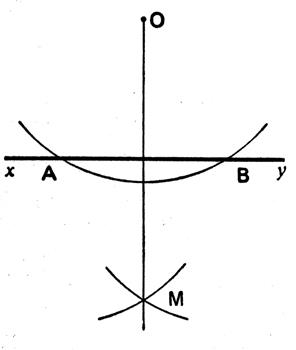
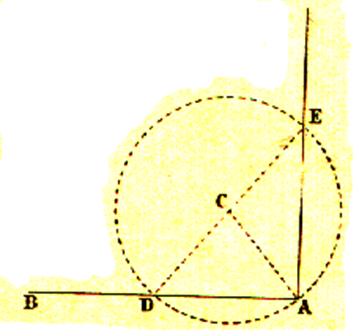
Soit une droite donnée AB , à laquelle il faut élever une perpendiculaire au point A . On prend au dessus de AB un point quelconque C comme centre , et avec une ouverture de compas égale à CA , on décrit une circonférence qui coupe la droite AB au point D ; on tire une droite passant par les points D et C , que l’on prolonge jusqu’au point E , où elle rencontre la circonférence , et l’on mène la droite EA , qui est perpendiculaire à AB.
Voir les propriétés du triangle rectangle ; et son cercle circonscrit

Autre construction :

TRAVAUX AUTO FORMATIFS.

CONTROLE: (aucun)

EVALUATION:

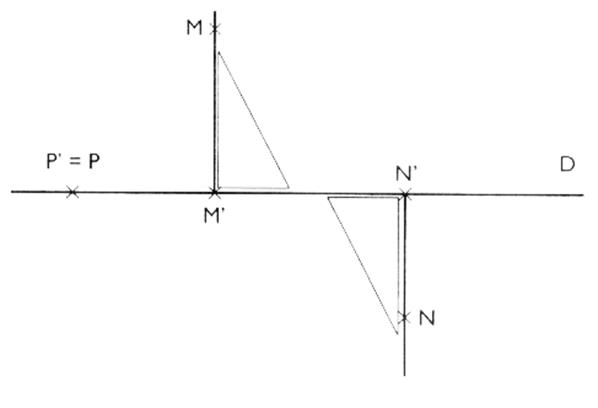
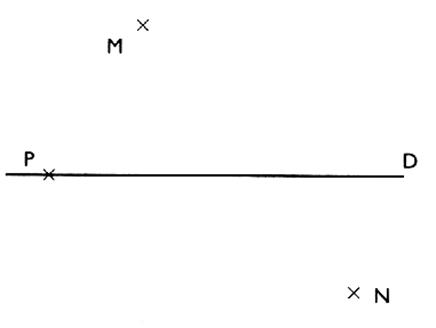
1°) Construire avec une équerre les perpendiculaires passant par les points M ;N ; P

Activités

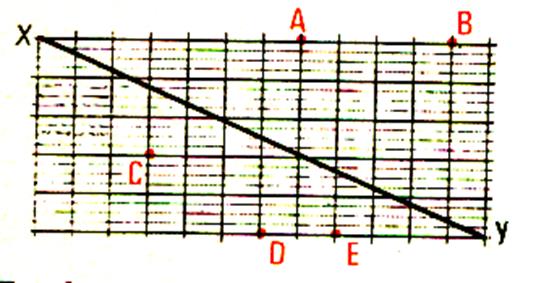
1°) Par les points A ; B ; C ; D ; E ;

Mener des perpendiculaires à xy

Mesure d’un angle  : (voir le rapporteur d’angle)

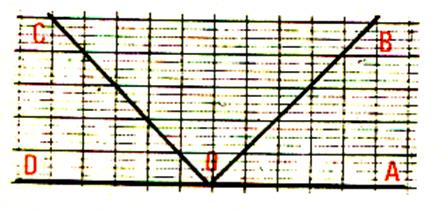
3°) Reproduire la figure : Mesurer l’angle BOA ; l’angle COB ; l’angle COD ; l’angle DOB , ; l’angle COA .

Mesure d’angle ; tracer d’un demi carré ou triangle isocèle

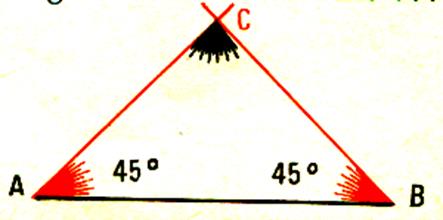
4°)Traçons un segment de droite AB . Dessinons avec un rapporteur 2 angles de 45° ayant pour sommets A et B .Les côtés de ces angles se coupent en C . mesurer l’angle « C » Les segments AC et BC sont ……………………………..

5°) A l’aide de l’équerre ; reconnaître dans les dessins suivants les lignes perpendiculaires : (entourer le numéro des dessins dont les lignes sont perpendiculaires.

Niveau 1 :

En vous aidant des dessins , refaire ces tracés :

sur une autre feuille donner l’ordre des tracés.

1°) Elever une perpendiculaire sur le milieu d’une droite

2°) Elever une perpendiculaire à une droite par un point donné sur cette droite.
3 ° ) Par un point A , pris hors d’une droite CB , abaisser une perpendiculaire à cette droite.

4°) Elever une perpendiculaire à l’extrémité A d’une droite AB , qu’on ne peut prolonger

5°) Elever , par un autre moyen , une perpendiculaire à l’extrémité d’une droite qu’on ne peut prolonger.

Niveau 2 :

1°) Elever une perpendiculaire sur le milieu d’une droite

2°) Elever une perpendiculaire à une droite par un point donné sur cette droite.

3 ° ) Par un point A , pris hors d’une droite CB , abaisser une perpendiculaire à cette droite.

4°) Elever une perpendiculaire à l’extrémité A d’une droite AB , qu’on ne peut prolonger.

5°) Elever , par un autre moyen , une perpendiculaire à l’extrémité d’une droite qu’on ne peut prolonger.

INTERDISCIPLINARITE : applications

Travail sur feuille de métal ou plaque .(les bords ne pouvant servir de départ de traçage .

Comment tracer une droite perpendiculaire à une autre droite tracée , le plus prés possible des deux bords

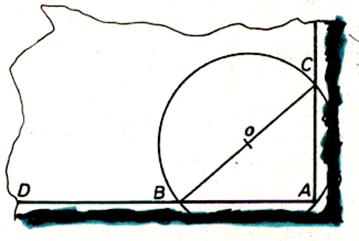
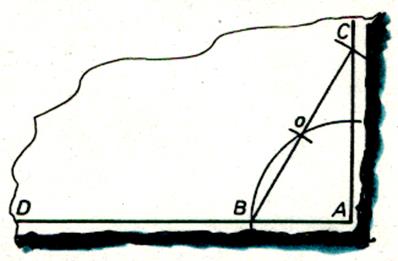
Premier procédé :

D’un point O quelconque , décrire le cercle de rayon OA . ( une partie du cercle peut-être en dehors de la feuille ) Ce cercle coupe la droite D en « B » , joindre OB qui coupe le cercle en « C » Tracer AC . ( justification / ? ? ?Info )

/

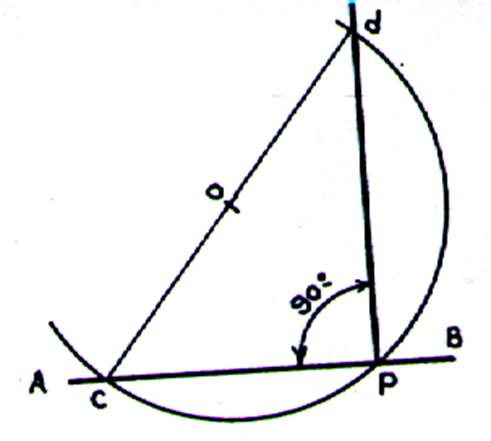
Deuxième procédé :

Tracer la droite « D » ; tracer du point A ( choisi arbitrairement) un arc de cercle de rayon quelconque coupant la droite en B . Tracer de B un arc de cercle de même rayon coupant le premier en O. Joindre BO et prolonger en portant avec le compas une longueur OC égale à BO. Tracer AC ( le point A est sur le cercle de diamètre BC ).

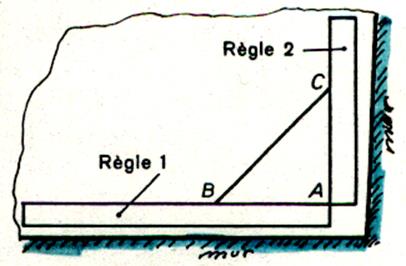
Troisième procédé :

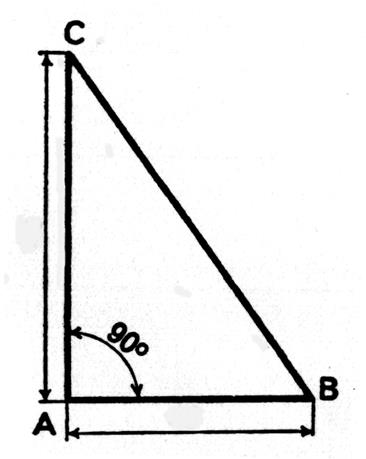
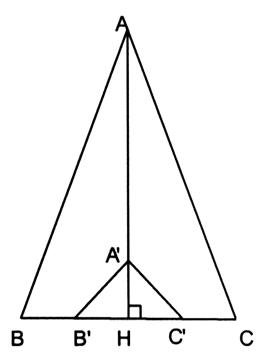
Ce procédé est employé dans le bâtiment , par exemple pour le pavage d’une pièce. On mesure AB = 6O cm sur la règle 1 , qui sert de base , puis on mesure AC = 80 cm sur la règle 2 , et on déplace la règle 2 de façon que BC mesure 1m. Les deux bords AB et AC forment un angle droit.

Remarques : Sur une surface plus réduite , on pourrait porter

AB = 6 cm AC = 8 cm ; il faut que BC mesure 10 cm .

Ou AB = 3 cm AC = 4 cm ; il faut que BC mesure 5 cm .

Ou AB = 12 cm AC = 16 cm ; il faut que BC mesure 20 cm .

Cliquez ici pour : INFO ++++ sur le triangle rectangle «  3 ;4 ;5 » et « Pythagore »

CORRIGE :

Evaluation:

1°) Construire avec une équerre les perpendiculaires passant par les points M ;N ; P