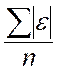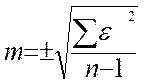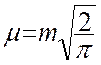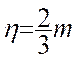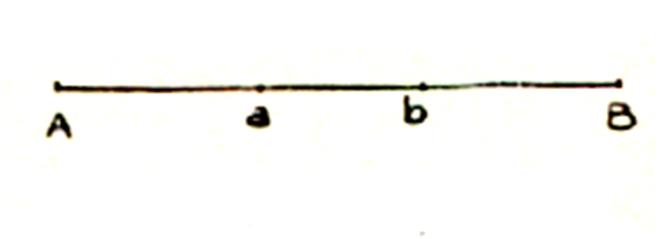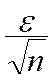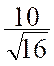Pré requis:

- Voir la définition des mots « faute » et « erreur » dans le dictionnaire.

- Ordres de grandeur

ENVIRONNEMENT du dossier:

Index	AVANT : Nomenclature ..	COURS	Complément d’Info : - Liste des cours sur : Le calcul numérique. - Info sur leçons disponibles sur les statistiques.
	Document à lire et à s’imprégner……………….

TITRE : NOTIONS sur les fautes et les erreurs.

1. distinction entre fautes et erreurs.

2. Les erreurs systématiques.

3. Les erreurs vraies et erreurs apparentes .

4. La loi de probabilité des erreurs accidentelles.

5. Les erreurs accidentelles ( caractéristiques)

6. La combinaison d’erreurs accidentelles.

Travaux ; devoirs			Corrigé
TEST	Contrôle	évaluation	Contrôle	évaluation

Interdisciplinarités : (matière concernée) : L’arpentage ou topographie
F	H	Géo.	Vie quotidienne et vie familiale	Autres :	Sciences et technique	Physique Chimie Electricité	Statistique.

COURS

I) Distinction entre fautes et erreurs.

Les fautes , au sens des mesures physiques et topographiques , sont des imperfections évitables ,généralement grossières , dues à des inadvertances opératoires qu’une organisation judicieuse et une discipline plus stricte dans les travaux eussent permis de déceler et d’éliminer .

Les erreurs , au contraire , sont des inexactitudes inévitables dues à l’imperfection des sens et des instruments .

Ce sont ces dernières seules qui entrent dans le cadre des lois statistiques des probabilités .

La connaissance des lois de leur combinaison est fondamentale pour le géomètre topographe et les responsables en métrologie , car ce sont celles qui conditionnent l’organisation même de leurs travaux .

Aussi , connaissant les procédés et les instruments de mesure ( en topographie par exemple) , il ne sera possible de juger d’une méthode opératoire , (relative à un relevé déterminé), qu’à la lumière des règles d’appréciation de l’influence des erreurs .

II) Les erreurs systématiques.

Les erreurs systématiques suivent des lois généralement connues et de sens connu . Par exemple , les mesures faites avec une chaîne de 20 m trop courte de 5 mm seront entachées d’une erreur systématique ; son importance et son signe sont connus si l’étalonnage nécessaire a été fait , et son influence peut s’éliminer par la correction conséquentes des mesures effectuées.

En résumé , les erreurs systématiques peuvent être , en général , déterminées et leurs influences éliminées par des méthodes d’observation adaptées .

III )Les erreurs vraies et erreurs apparentes .

Quelle que soit la source d’erreur , elle s’estime , théoriquement , par la différence d’une mesure effectuée avec celle de la valeur parfaite que l’on eût dû trouver ; c’est ce que l’on nomme les « erreurs vraies ».

Mais ces « erreurs vraies » ne sont , pratiquement , jamais connues , puisque la connaissance de la valeur parfaite échappe à l’observateur.

On porte donc intérêt aux « erreurs apparentes » , que l’on désigne encore par « résidus » et que , seules , on peut estimer par l’écart de chaque mesure avec la moyenne d’un certain nombre de mesures semblables du même objet.

Par exemple , nous mesurons vingt fois la largeur d’une table , avec un mètre étalonné , au maximum de la précision que l’œil permet . Nous ne connaissons pas la valeur parfaite de cette longueur , mais il est raisonnable d'admettre que sa valeur la plus probable est la moyenne arithmétique des vingt mesures effectuées . A partir de cette valeur , nous tirons vingt écarts entre celle-ci et chacune des vingt mesures qui sont intervenues : ce sont des « résidus » ou « erreurs apparentes ».

En fait , dans la suite de cet exposé , il ne sera implicitement question que d’erreurs « apparentes » .

IV) La loi de probabilité des erreurs accidentelles.

Les erreurs apparentes accidentelles sont celles que l’organisation opératoire n’a pas permis d’éliminer , car la nature profonde n’est pas connue .

Si l’on voulait une comparaison , on pourrait la prendre dans le domaine médical . On reste impuissant devant une maladie dont le virus n’a pas été isolé ; nous sommes alors devant l’impondérable que l’on abandonne au domaine statistique ; par contre , si cet isolement a été possible , la lutte contre la maladie prend généralement son efficacité : nous entrons dans le domaine de systématisme opératoire . La seconde phase représente un progrès sur la première , comme , pour le topographe , le fait de faire passer une erreur accidentelle dans le domaine des erreurs systématiques , après avoir compris sa source et annulé son effet .

IL est , en effet , possible que le caractère accidentel des erreurs opératoires ne soit qu’une expression de notre ignorance des lois compliquées de certaines erreurs systématiques .

Mais il est remarquable d’observer que , traitées dans leur ensemble , ces erreurs accidentelles sont justifiables de lois statistiques de probabilités qui constituent ce que l’on nomme la « théorie des erreurs ».

On présuppose tout d’abord que le nombre d’observations de même nature est grand et , pour une mesure donnée , on observe que :

1°) la valeur absolue de l’erreur est limitée supérieurement : donc , à partir d’une certaine valeur , il s’agit toujours d’une faute et jamais d’une erreur ;

2°) les plus petites valeurs des erreurs , comptées en valeurs absolues , sont les plus nombreuses ;

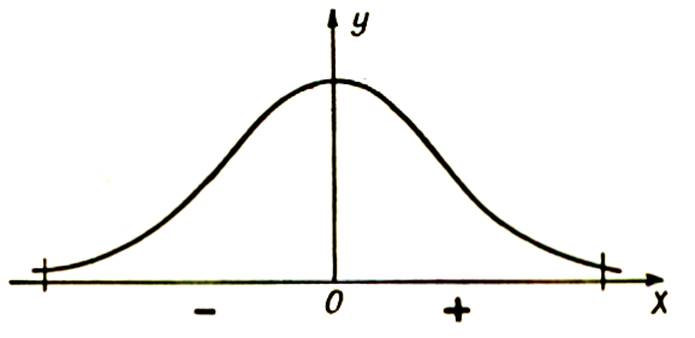
3°) A toute erreur positive donnée doit correspondre , approximativement , une erreur négative .

Nous pouvons exprimer ces constations par une courbe ( de Gauss) construite avec :

- pour abscisses , la valeur des erreurs avec leur signe , de part et d’autre de l’origine 0 ;

- pour ordonnées , le nombre d’erreurs trouvées répondant aux valeurs exprimées sur l’axe des abscisses.

C’est la courbe « en cloche » de Gauss qui a , au début du XIXe siècle , établi la théorie mathématique de ces probabilités .

Imaginons que nous fassions un grand nombre de fois la même mesure et que construisant une telle courbe , on la constate asymétrique par rapport à l’axe 0y ; cela signifiera que toutes les erreurs ne répondent pas aux lois accidentelles ci-dessus mentionnées , donc que des erreurs systématiques subsistent dans les mesures ; on en conclura que le mode opératoire est à réviser et à parfaire . Cette remarque montre qu’il est pratiquement souhaitable et profitable de faire la construction d’une courbe en « cloche » spécifique de certaines mesures . Tout ce qui va être dit concernant les erreurs accidentelles n’est valable que si cette nature accidentelle est assurée.

La forme de la courbe d’une série opératoire exprime une certaine loi de probabilités .

V ) Les erreurs accidentelles ( caractéristiques)

Il est raisonnable et commode de définir la précision d’une opération de mesure par certaines valeurs d’erreurs accidentelles , caractéristiques de la loi de probabilité à laquelle elle se rapportent . Nous donnerons la définition des plus usités ( sans donner la genèse mathématique de leur intervention)

a) L’erreur moyenne arithmétique .

L’erreur moyenne arithmétique qui est la plus simple des références de précision , est couramment appelé « erreur moyenne » ; c’est la moyenne arithmétique des ( n ) erreurs ( notée : m ) où les résidus élémentaires ( e ) sont pris en valeur absolue , soit :

m =

b) l’erreur moyenne quadratique .

L’erreur moyenne quadratique définit avec plus d’exactitude la précision d’opérations de mesures : c’est la racine carré du quotient de la somme des carrées des erreurs ( e ) par le nombre ( n ) de ces erreurs ou résidus , moins 1 , soit :

c) l’erreur probable .

L’erreur probable est telle qu’en valeur absolue , et dans une série de mesures équivalentes , il y avait autant de chances d’en commettre une plus forte qu’une moins importante .

En d’autres termes , si l’on considère une suite d’écarts en valeur absolue , l’erreur probable h est la valeur de l’écart qui sépare autant d’écarts inférieurs que d’écarts supérieurs à lui .

d) L’erreur maximum (e_m )

L’erreur maximum (e_m ) est celle qu’il y a si peu de chances de commettre qu’une valeur supérieure peut-être qualifiée de faute .

Dans une série d’ erreurs apparentes  ( résidus) de mesures dégagées d’erreurs systématiques , c’est à dire répondant à la loi de Gauss , on démontre que les diverses erreurs ont entre elles les relations suivantes :

Si :

m est l’erreur moyenne arithmétique ;

m est l’erreur moyenne quadratique ;

h est l’erreur probable

e_m est l’erreur maximum

on a »

»

e_m = 3,5 h = 2,5 m

Exemple numérique .- Soit une série de mesures ayant fourni les résidus suivants par rapport à leur valeur moyenne :

-8 + 9 + 4 –11 – 9 + 12 + 17 – 6

- L’erreur moyenne arithmétique est …………………. m = 9,5

- L’erreur moyenne quadratique est ……………………m = 11,0

- L’erreur probable est ………………………………..h = 9,0

- L’erreur maximum est ………………………………e_m = 27,5

Il est à remarquer que les rapports théoriques entre les différentes erreurs caractéristiques ne sont respectés , dans les hypothèses fondamentales , que pour une série d’un grand nombres d’écarts .

VI ) La combinaison d’erreurs accidentelles.

Nous énumérons simplement , sans les démontrer , les règles des combinaisons des erreurs accidentelles .

a) l’erreur moyenne quadratique « m » d’une somme de terme ayant chacun des erreurs quadratiques connues e₁ ; e₂ ; e₃ ….est donné par :

m =

Exemple .

Nous cherchons l’erreur moyenne quadratique d’une longueur AB (voir dessin) composée de trois tronçons Aa , ab , bB , mesurés chacun plusieurs fois mais avec des précisions différentes , dépendant par exemple des difficultés du parcours . Soient :

e₁ = 10 cm e₂ = 5 cm e₃ = 7 cm

Les erreurs moyennes quadratiques des longueurs moyennes trouvées respectivement pour ces trois tronçons ; l’ erreur moyenne quadratique de leur somme , c’est à dire de la longueur AB , sera :

m = = 13 cm

b) l’erreur moyenne quadratique « m » d’une somme de « n » termes ayant chacun des erreurs moyennes quadratiques connues et égales à e , est donnée par :

m = e

C’est ,en fait, le cas particulier du problème précédent qui se présente le plus fréquemment dans la pratique .

Exemple : reprenons l’exemple précédent de la longueur de AB .Si les trois tronçons avaient été mesurés chacun plusieurs fois avec une erreur moyenne quadratique égale à e = 10 cm , pour chacun d’eux , on aurait pour erreur moyenne quadratique de leur somme AB :

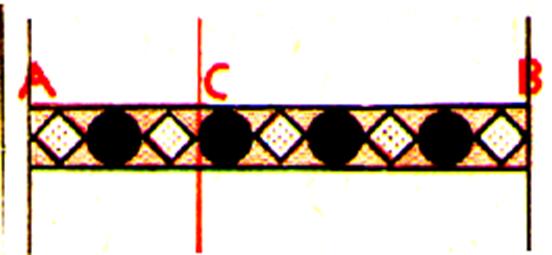
m = 10 = 17 cm

c) l’erreur moyenne quadratique :

L’erreur moyenne quadratique « m » d’une différence de termes d’erreurs moyennes quadratiques connues e₁ ; e₂  est donné par :

m =

Exemple :

Un tronçon égal à la différence des tronçons et , mesuré plusieurs fois et dont les erreurs moyennes quadratiques sont respectivement : e1 = 10 cm et e2  = 5 cm

L’erreur moyenne quadratique du tronçon sera :

m = = 11 cm

d) l’erreur moyenne quadratique « m » de la moyenne arithmétiques de « n » termes d’erreurs moyennes quadratiques connues et toutes égales à e est : e

m =

Exemple : mesure d’un angle : Si l’on fait un certain nombre de fois ( seize par exemple) la mesure d’un même angle avec une précision répondant à la même loi de probabilité d’erreur moyenne quadratique e = 10’’ , l’erreur moyenne quadratique de la moyenne des seize mesures effectuées sera :

m = = 2,5’’

Remarques importante : les considérations relatives aux erreurs accident telles n’ont pas de caractère rigoureusement absolu ;elle se rattachent à la théorie des probabilités.

De toutes façons , elles n’ont de signification raisonnable que si l’on respecte les deux hypothèses fondamentales et préalable , à savoir :

a) les mesures sont expurgées des erreurs systématiques ;

b) Elles sont effectuées en grand nombre ; deux ou trois mesures ne rentre pas dans cette catégorie.

CONTROLE:

- A créer ! ! ! ! Que veut – on que sache l’élève ?

EVALUATION:

Reprendre les exercices traités dans le cours ! ! ! ! ! !