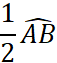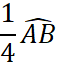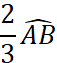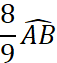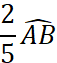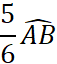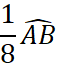Lecture : Rappels : les figures géométriques sont limitées par des lignes. Ces lignes sont « droites » (tracées à la règle) , soit « courbe » (tracées au compas ) . Mesure de la longueur d’une ligne : « Ligne droite » :Mesure de la longueur d’une droite : directement avec une règle graduée ; La mesure de la longueur d’une droite s’obtient par calcul : voir « calcul de la mesure d’un segment sur un axe »  ou « calcul de la mesure d’un segment dans un repère. » « ligne courbe » : sa longueur peut s’obtenir par mesure : on pose un fil sur la ligne courbe ; puis on la tend ce fil , on mesure à la règle . Si la courbe est un cercle : faire le calcul de la longueur de la circonférence. Si la courbe est un arc de cercle : on peut obtenir la longueur par calcul  : il faut connaître le rayon du cercle ,la longueur de l’arc en degré ,la relation mathématique qui lie le calcul du périmètre du cercle et la partie d’un angle d’un arc.
Pré requis :
Notions : plan –ligne – point		Primaire/collège
Matériel de traçage		Info
Le nombre "pi"		Info
La ligne courbe		(primaire)
ENVIRONNEMENT du dossier:
				Classe 6^ème
Index : warmaths	Objectif précédent : Le segment. Le cercle ( découverte) Le cercle et le disque ( au collège 6^ème )		Objectif suivant : 1°) Le cercle 2°)Les disques 3°) détermination du centre 4°)positions relatives de deux cercles 5°) positions relatives d’un cercle et d’une droite 6°) Les arcs….	1. Géométrie présentation 2. Arithmétique et géométrie 3. >>> Dossier : dessins 4. Programme de la classe de 6^ème collège.
DOSSIER « géométrie » cercle et disque » : LA LONGUEUR DU CERCLE

1° )Le nombre « pi » () (Découverte)

2°) Longueur du cercle.

3°) Calculs d’application .

4°) Mesure en degré d’un arc de cercle .

Valeur de l’angle au centre , Arc de même mesure.

5°) Longueur d’un arc de cercle.

					Voir le corrigé de la fiche ……..
TEST CLASSE 6éme	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité ►Sciences ►Situations problèmes. ► dossier n° sur le cercle …..	Corrigé Contrôle	Corrigé évaluation
COURS

1°) Le nombre « pi » () (Découverte)

Faire des mesures à la maison. (soit avec un mètre à ruban souple , ou entouré le volume avec un ficelle puis mesurer la longueur développée .) Procurez-vous des objets présentant une partie circulaire : boite de conserve, roue tuyau, tonneau cylindrique, assiette, verre, tube …. Avec la même unité de longueur pour chaque objet (ce qui signifie que les dimensions d’un même objet doit avoir été mesurés dans la même unité de longueur ( tout en mm, ou tout en cm ; ou tout en …..) , on vous demande d déterminer la mesure du diamètre ( d )et la mesure « L » de la longueur du cercle correspondant , ensuite vous faîtes le quotient ( division) de « L » par « d » Nota : · ne dépassez pas deux chiffres après la virgule.. · Utilisez le tableau ci –dessous et y placer les résultats.. ;

Les objets

L

« d »

« L : d »

1°)……………………

2°)……………………

3°) ………………….

4°)…………………...

· Faîtes la moyenne des 4 quotients que vous avez trouvés :

Pour calculer la moyenne il faut additionner les 4 quotients et ensuite diviser le nombre trouvé par « 4 »

Moyenne : ……………………………………..

· Si l’on regroupe les résultats de tous les élèves et si l’on fait la moyenne on obtient :……………………………………………………

Pour calculer la moyenne il faut additionner les quotients et ensuite diviser le nombre trouvé par le nombre d’élèves.

Moyenne : ………………………………………

· Ce nombre est une valeur approchée du nombre «   » ( lettre grecque qui se lit « pi »)

Le nombre «   » est un nombre ayant une infinité de chiffres après la virgule , en voici le début : 3,1415926535897932384626433832795…………………….

· Pour les calculs, on utilise des valeurs approchées de «   » avec plus ou moins de précision.

complétez

3 < < 4

3,141 < < ……………

3,1 < < 3,2

……………. < < ……………

3,14 < < ……………

……………. < < ……………

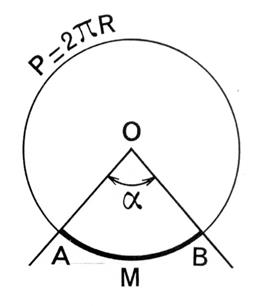
2°) Longueur du cercle. (info ++)

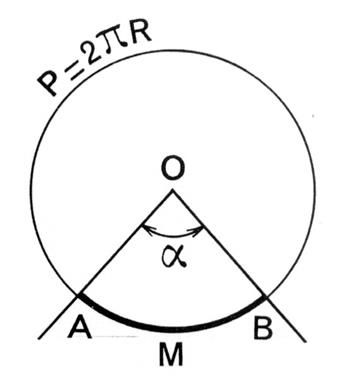
Vous venez de constater que pour tout cercle, si l’on divise la longueur « L » par « d » , on trouve un nombre voisin de «  ». Les mathématiciens ont prouvé que , quelque soit le cercle considéré, le quotient de « L » par « d » est exactement le nombre «  ».

On écrit alors

L d =

C'est-à-dire

L = …….………..

· Appelons « R » la mesure du rayon du cercle. Sachant que « d = 2 R , on peut écrire que «  L = 2 R  » ou bien encore «  L = 2 R »

· Connaissant la mesure de la longueur du cercle , o peut déduire la mesure du diamètre ou la mesure du rayon :

«  d = ………………….. »

«  R =………………….. »

3°) Situations problèmes et exercices.

Dans tous les cas vous prendrez pour «  » : le nombre «  3,14 » comme valeur approchée de pi.

Exercice 1 : Calculez le diamètre d’un cercle dont la longueur est « 21,98 m»

Exercice 2 : Calculez le rayon d’un cercle dont la longueur est « 21,98 m»

Problème 1 :

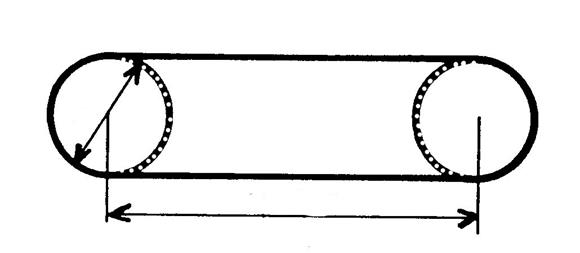
Le dessin ci-contre représente deux poulies (cercles) et la courroie qui les réunit . Le diamètre de chaque poulie est de 30 cm, la distance des centres des poulies est de « 1,86 m » ; calculez la longueur de la courroie.

Problème 2 :

Le tour de la terre est d’environ « 40 000 km ». Calculez une valeur approchée à 10 km près du rayon de la terre.

Problème 3 :

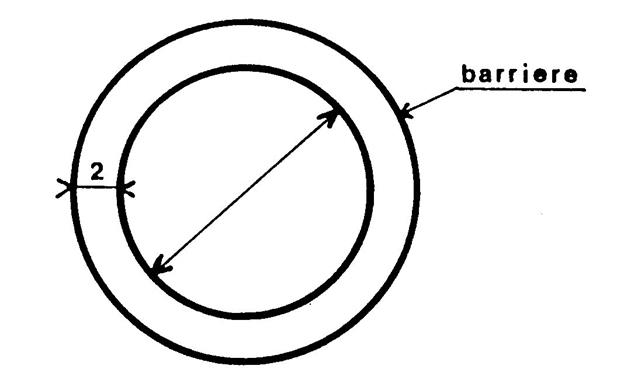
Un bassin circulaire de 32 m de diamètre est entouré par une barrière circulaire .( vois ci contre) Cette barrière est située à 2 m du bord du bassin. Calculez la longueur de la barrière.

Problème 4 :

Les roues d’un vélo ont un diamètre de 100 cm. Quel est le développé d’un tour de roue ?

Problème 5 :

Le diamètre des roues d’une automobile est de 50 cm. Combien de tours ( à 10 tours prés) fera chaque roue pour effectuer un parcours de 1 km. ?

Problème 6 :

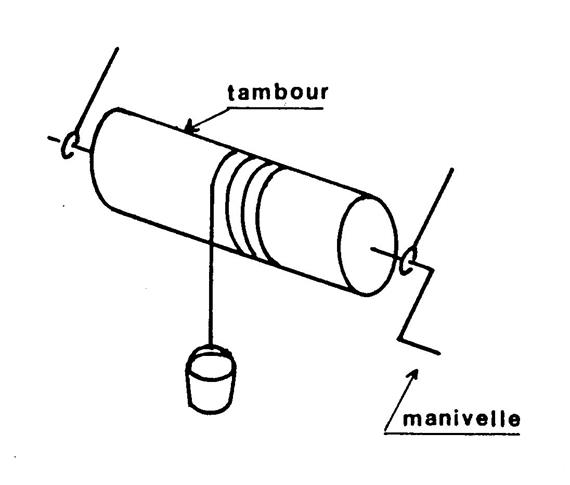
Ci-contre on vous donne le schéma de treuil….( chaque tour est assimilé à un cercle). En tournant la manivelle, la corde s’enroule sur le tambour et on peut faire descendre ou monter un seau . Le diamètre du tambour est de 20 cm. 1°) de combien est descendu l’objet quand on fait 10 tours de manivelle ? 2°) Combien faut-il faire de tour de manivelle pour que le seau monte de « 9,42 m » ?’

4°) Mesure en degré d’un arc de cercle.

a) Valeur de l’angle au centre

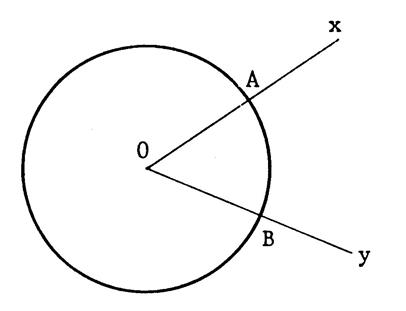
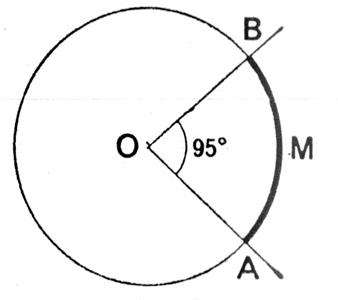
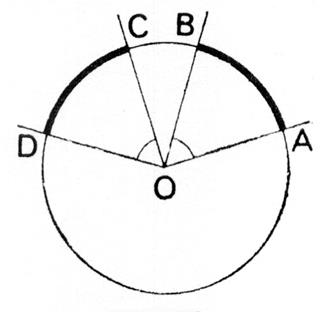
Voici un cercle de centre « O ». est un angle dont le sommet est au centre du cercle. On l’appelle « angle au centre ». Il détermine sur le cercle un arc : l’arc AB noté : Par convention , on décide de prendre pour mesure de l’arc (en degré). La mesure en degré de l’angle «  »

Mesure de = mesure de l’angle «  » (en degré)

Exemple : sur le dessin, on a «  » = 56 ° , on écrira alors l’angle décrit par l’arc = 56 °

b ) Arc de même mesure.

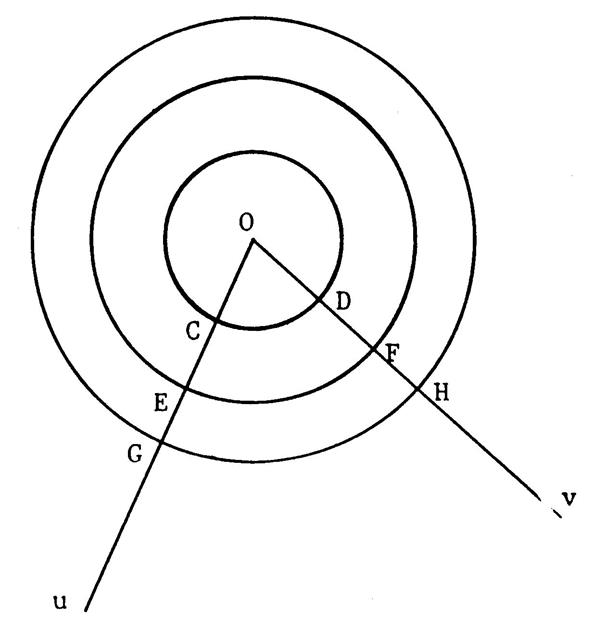
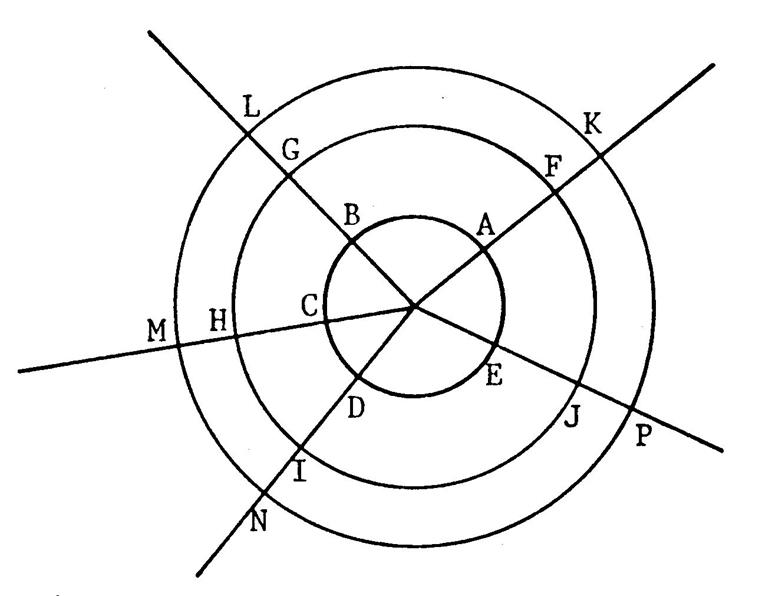
Sur la figure ci-contre on vous donne des cercle concentriques de centre « O ». Les arcs :  ;  ; correspondent à la même valeur d’angle que l’angle . Activité : Mesurez .. Vous trouvez : .= ………………..° On peut donc écrire : L’ arc  = …………°….;  =……………°…; =……………°…..

Attention : Bien qu’ayant la même mesure, ces arcs ne sont pas superposables. Des arcs de même mesure sont superposables uniquement dans le cas où ils sont situés sur un même cercle ou sur des cercles de même ..rayon… Voir ci –contre. Ci- dessous si : = les arcs sont superposables…..

c ) Arcs particuliers .

· Le cercle correspond à l’angle plein , sa mesure es degré est de ………… · Le demi-cercle correspond à l’angle ………. … , sa mesure en degré est de ………. · Le quart de cercle ( appelé aussi « quadrant ») correspond à l’angle …………………..sa mesure est de « ………….. ».

Activité :

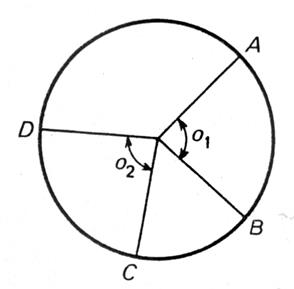
Complétez le tableau donnant la mesure d’arcs représentés sur la figure ci-contre. ( Les arcs considérés sont ceux qui correspondent à des angles saillants). Faites les mesures à 1° prés.

Arc

Mesure.

5°) Longueur d’un arc de cercle.

Vous savez calculer la longueur d’un cercle. (voir ci -contre ) Un arc de cercle étant une « portion » d’un cercle. Il est possible d’en déterminer sa longueur connaissant sa mesure en degré. Exemple : On donne un cercle dont le diamètre est de 400 mm En prenant pour «  » la valeur approchée « 3,14 ». : - La longueur de ce cercle est de …………………………..…… - La longueur du demi-cercle est de ……… …………………. - La longueur du quart de cercle est de ……… …………….

· Sachant qu’un arc de « 1° » correspond à du cercle. Quelle est la longueur d’un tel arc ( 1°) sur le cercle précédent ( à 0,01 mm prés ) ? Quelle est la longueur d’un arc de 73° sur le même cercle ( à 1 mm prés )

Activité .. : La longueur d’un méridien terrestre ( tour complet) est de « 40 000 km ». Déterminez sur celui-ci la longueur d’un arc de « 1° » ( au km prés) :

Déterminez la longueur ( à 10 m prés) d’un arc de « 1’ » (lire « une minute ») sachant que « 1° = 60 ‘ »

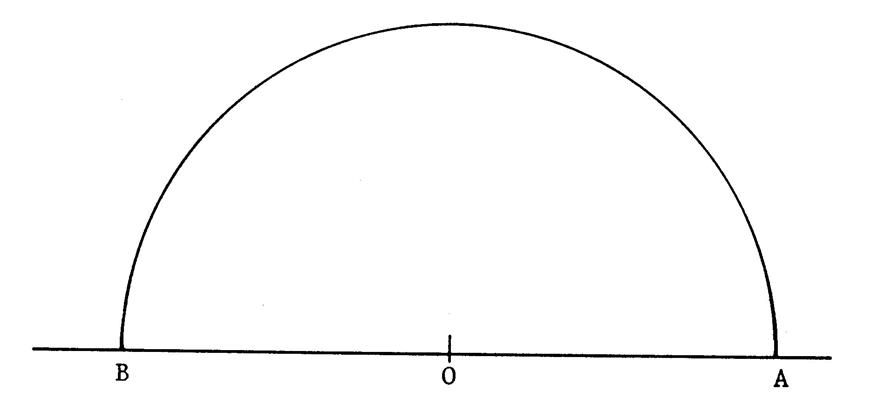
Activité .. : Voici un demi-cercle de centre « O » et de diamètre [ AB ] tel que « AB = 90 mm »

Calculez la longueur de ce demi-cercle . ( = 3,14) ………………………………………………………………………………………………………………………..

Complétez le tableau ci-dessous puis placez , sur le demi-cercle ci-dessus , les points « C » , « D » , « E » , « F » , « G » , « H » et « J » en utilisant les données de ce tableau.

Exemple : Le point « C » est défini par l’arc , tel que l’arc = · Puisque l’arc AB = 180° , alors l’arc AC = 90° , donc l’angle = ………….……Placez le point. Placez le point C. · Puisque la longueur du demi-cercle est de 141,3 mm , alors la longueur de l’arc est égale à « 141,3 2 » c'est-à-dire ….. …….. »

Arc

Correspondant avec

Mesure en degré

Longueur en mm.

Préparation du devoir ;TRAVAUX AUTO - FORMATIFS
CONTROLE :
EVALUATION :
3°) devoir de tracés : cliquez ici	( à imprimer )