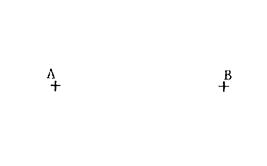Lecture : Rappels : les figures géométriques sont limitées par des lignes. Ces lignes sont « droites » (tracées à la règle) , soit « courbe » (tracées au compas ) . Mesure de la longueur d’une ligne : « Ligne droite » :Mesure de la longueur d’une droite : directement avec une règle graduée ; La mesure de la longueur d’une droite s’obtient par calcul : voir « calcul de la mesure d’un segment sur un axe »  ou « calcul de la mesure d’un segment dans un repère. » « ligne courbe » : sa longueur peut s’obtenir par mesure : on pose un fil sur la ligne courbe ; puis on la tend ce fil , on mesure à la règle . Si la courbe est un cercle : faire le calcul de la longueur de la circonférence. Si la courbe est un arc de cercle : on peut obtenir la longueur par calcul  : il faut connaître le rayon du cercle ,la longueur de l’arc en degré ,la relation mathématique qui lie le calcul du périmètre du cercle et la partie d’un angle d’un arc.
Pré requis :
Notions : plan –ligne – point		Primaire/collège
Matériel de traçage		Info
Le nombre "pi"		Info
La ligne courbe		(primaire)
ENVIRONNEMENT du dossier:
				Classe 6^ème
Index : warmaths	Objectif précédent : Le segment. Le cercle ( découverte)		Objectif suivant : 1°) Le cercle 2°)Les disques 3°) détermination du centre 4°)positions relatives de deux cercles 5°) positions relatives d’un cercle et d’une droite	1. Géométrie présentation 2. Arithmétique et géométrie 3. >>> Dossier : dessins
DOSSIER « géométrie » cercle et disque » : LE CERCLE et le DISQUE.

1. DISTANCE DE DEUX POINTS.

2. CERCLE

3. DISQUE

TEST CLASSE 6éme	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité ►Sciences ►Situations problèmes. ► dossier n° …..	Corrigé Contrôle	Corrigé évaluation
COURS

1°)	DISTANCE DE DEUX POINTS.
	Ci contre on vous donne deux points « A » et « B » . On vous demande de tracer le segment [ AB]. L’unité étant le « mm », mesurer la longueur du [ AB]. Vous trouvez , après mesure , le nombre de : …( 57 mm)est la distance relevée sur « mon » écran) ……………… Ce nombre est aussi appelé la « distance de A à B ».
	Donc on utilise la même notation pour désigner une longueur et une distance.
	AB = 57 mm ; c’est une longueur .
	AB = 57….c’est :				La mesure de la longueur
					La distance qui sépare A de B L’unité est ici le « mm »
2°)	CERCLE
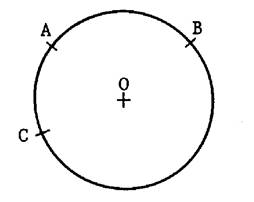
	Ci contre on vous donne un cercle : « O » est appelé « le centre du cercle ». « A », « B » et « C » sont des points du cercle. [ OA ] , [ OB] et [ OC] sont des rayons de ce cercle. ( exemple : le rayon est une corde tendue ) Ces rayons ont tous la même longueur . ( la longueur correspond à l’ écartement des branches de compas) . On peut écrire alors : OA = OB = OC. ; etc. Le mot « rayon » désigne aussi la longueur (commune) de tous ces segments. ( Ou la mesure de cette longueur , une unité étant choisie)
	On retiendra : Une unité de longueur étant choisie , « O » étant un point du plan et « R » un nombre, on appelle « cercle » de centre « O » et de rayon « R » l’ensemble des points du plan situés à la distance « R » du point »O ».
	Si « N » est un point du cercle de centre « O » et de rayon « R » signifie que « ON = R »
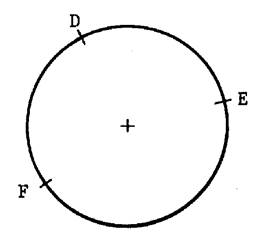
Info 2 ++	« corde » Sur le cercle ci contre on a placé 2 points « D » et « E ». On vous demande de tracer le segment [ DE] . Ce segment est appelé une « corde » Tracer toutes les cordes possibles ayant pour extrémité le point « F » et pour longueur 30 mm . Combien en comptez vous ?
	« Diamètre » Parmi les cordes , il y en a certaines qui passent par le centre , on les appelle des « diamètres » On vous demande de tracer sur la figure ci-dessus le diamètre dont l’une des extrémités est « D ». Remarque : « diamètre » désigne aussi la longueur ou la mesure de la longueur d’une telle corde.
Info1 +++	« arcs de cercle »
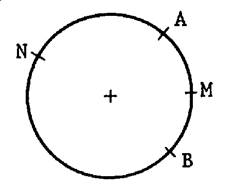
	On vous demande de tracer en rouge la portion de cercle limitée par « A » et « B » ; ce tracé représente l’arc de cercle , on le note :
	La portion de cercle qui n’est pas coloriée en rouge est aussi un arc de cercle qui se note ,aussi ,
	Pour distinguer ces deux arcs , on peut utiliser un point appartenant à l’arc considéré : Le petit arc sera noté l’arc « AMB » surmonté d’un arc ; le grand arc AB sera noté « ANB » surmonté d’un arc.
Info++	3°) DISQUE
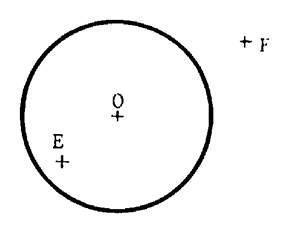
	Ci contre vous avez un cercle de centre « O » et de rayon « R ». « E » est à l’intérieur du cercle ; et « OE < R » « F » est à l’extérieur du cercle , et « OF > R » Passez en rouge l’ensemble des points du plan dont la distance au centre est inférieure ou égale au rayon. L’ensemble de ces points est appelé « disque » : le disque de centre « O » et de rayon « R ».
	Exercice 1 :
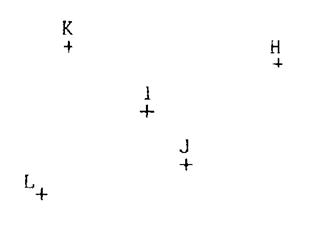
	Ci contre : On donne des points appartenant au même plan : « H ; I ; J ; K ; L »   et « IK = 17 mm ». On appellera « C  » le cercle et « D » le disque correspondant. : On vous demande de compléter le tableau ci-dessous en utilisant convenablement les symbole : et
	H …………… C	I…………… C	J…………… C			K …………… C	L…………… C
	H …………… D	I…………… D	J…………… D			K …………… D	L…………… D
	Exercice 2 :
	Voir ci contre : On a placé deux points « A » et « B » tels que AB= 44 mm Tracez un cercle de entre « A » et de rayon 30 mm et le cercle de centre « B » de rayon 20 mm
	1°) Placer un point « E » tel que , AE > 30 mm et BE = 20 mm. Coloriez en bleu l’ensemble des points tels que « E ».
	2°) Placer un point « F » tel que , AF < 30 mm et BF > 20 mm. Colorier en jaune l’ensemble des points tels que « F » .
	3° ) Placer un point « G » tel que AG < 30 mm , et BG < 20 mm. Colorier en vert l’ensemble des points tels que « G » .
	4° ) Placer un point « H » tel que AH = 30 mm , et BH < 20 mm. Colorier en rouge l’ensemble des points tels que « H » .
	5° ) Placer un point « K » tel que AK = 30 mm , et BK = 20 mm. Il existe un autre point tel que K . Appeler - le « L » . .
	Frise :
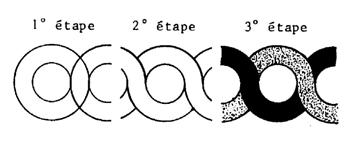
	Reproduire la frise ci-dessous sur toute la longueur de la feuille , en plaçant les centres sur la droite et en prenant pour rayon 10 mm et 20 mm. Colorier à votre guise.
2012	Ceci termine les activités sur les cercles et disques en 6^ème

Préparation du devoir ;TRAVAUX AUTO - FORMATIFS
CONTROLE :
I ) Donner les définitions des caractéristiques suivantes
centre
cercle
Rayon
diamètre
circonférence
disque
arc de circonférence
corde
Angle au centre
EVALUATION : 1°)Tracer un cercle de 10 cm de diamètre , ensuite tracer et nommer la flèche ; la corde , le diamètre , le centre, le rayon , une tangente et une sécante 2°) D’un point situé à 12 cm du centre d’un cercle de 6cm de rayon , on mène deux tangentes à ce cercle. Quel est leur angle ?
3°) devoir de tracés : cliquez ici	( à imprimer )