La circonférence.

Pré requis:

Le nombre "pi"
La ligne courbe

ENVIRONNEMENT du dossier:

Index « warmaths.fr »

Objectif précédent :

1°) Le cercle : notions..

2°) Le cercle

3°) Le cercle et le nombre « pi » en 6^ème au collège.

Objectif suivant

1°)Les positions entre plusieurs cercles

2°) Calcul de la longueur de la circonférence

3°) Le cercle et le disque (en 6^ème )

DOSSIER : LE CERCLE et La circonférence du cercle

1. Les éléments de la circonférence.
2. Voir aussi les droites particulières :
3. LONGUEUR de la circonférence du cercle :
4. Applications au cas courant :
5. ARC de cercle ou la DIVISION DE LA CIRCONFERENCE.
Informations « vers …….»
6. Longueur d’un ARC et d’une corde :
7. Mesure d’un angle
8. Angle inscrit dans une demi circonférence .
9. Le nombre « pi » : Ou rapport de la circonférence au diamètre .
10. CALCULS de la longueur d’un arc

		> travaux auto formatifs			>>corrigé des travaux auto – formatifs.
TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité	Corrigé Contrôle	Corrigé évaluation
				Fiche d’activités en arithmétique.
				Situations problèmes
				Statistique : le diagramme circulaire.

COURS

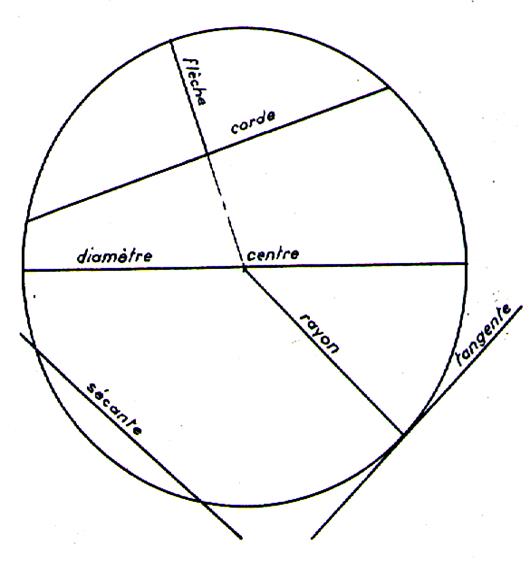
1°) Eléments de la circonférence :

Définition : La circonférence est une courbe fermée dont tous les points sont à égal distance d’un point appelé « centre ».

centre	Est un point intérieur du disque situé à égal distance de la circonférence.
cercle	Le cercle est l’ensemble des points de la circonférence.
Rayon	La distance du centre O à un point quelconque du cercle est le rayon.
diamètre	Le diamètre est une corde qui passe par le centre , sa mesure est le double de celle d’un rayon . Tous les diamètres sont isométriques . ( il partage le cercle ou disque en deux parties égales.)
circonférence	La circonférence est la frontière du disque.
INFO sur « disque »	Un disque est constitué par l’ensemble des points de la circonférence et de sa région intérieur.
arc de circonférence	Un arc de circonférence est une portion de circonférence limitée par deux points.
corde	Une corde est un segment de droite joignant deux points de la circonférence.
Angle au centre	Un angle au centre est un angle qui a pour sommet le centre du disque . On dit que l’angle « intercepte l’arc compris entre ses cotés » .

Les droites dans le cercle .

ins8

cercl

2°) Voir aussi les droites particulières :

Sécante :

Une sécante est une droite qui coupe la circonférence en deux points ; c’est une corde prolongée.

Info ++++

Tangente :

Une tangente est une droite qui n’a qu’un point commun avec la circonférence. Ce point est appelé « point de tangence , ou point de contact »

Info plus +++

3°) LONGUEUR de la circonférence du cercle : ( se rappeler que p =)

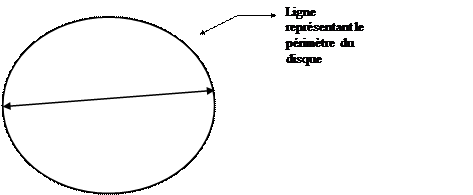
La longueur du cercle est égale au périmètre du disque P_d.

D

P_d= p D ou P_d= 2pR

ou sachant que D (Diamètre du cercle = 2 fois le rayon ) on peut aussi écrire que P_d= 2pR

4°) Applications au cas courant :

A savoir : La longueur du cercle est égale au produit de « pi » par la longueur du diamètre.

Formule (Modèle mathématique) : ( C pour longueur de la circonférence )

Calcul en fonction du diamètre

Calcul en fonction du rayon

C = 3,14 D

C = 3,142R

Ou (3,142= 6,28 )

C = = 6,28R

APPLICATIONS : INFO +++++

1 ) Calculer la longueur du périmètre du disque de 10 cm de rayon.

Corrigé :

a )inventaire de ce que je connais : C= 3,142R et R =10

b) On remplace dans C la valeur de R : C = 3,142 10

c) Calcul : 3,142 10 = 628

d) Conclusion : la longueur du périmètre du disque est de 628 cm

2 )Calculer la longueur du périmètre du disque de 10cm de diamètre.

Corrigé :

a )inventaire de ce que je connais : P_d= 3,14D et D =10

b) On remplace dans Pd la valeur de D : P_d= 3,1410

c) Calcul : 3,1410 = 314

d) Conclusion : la longueur du périmètre du disque est de 314 cm

5°) ARC de cercle ou la DIVISION DE LA CIRCONFERENCE.

1°) La circonférence se divise en quatre arcs égaux appelés « quadrants »

2°) Elle se divise aussi en 360 parties égales appelées « degrés »

Les degrés se partagent en 60 minutes , et les minutes en 60 secondes.

Rappels :

degrés , minutes et secondes s’indiquent respectivement par les signes ° ’ ’’

exemple :15 degrés 33 minutes 19 secondes s’écrivent : 15° 33’ 19’’

3°))Elle peut aussi se diviser en 400 partie égales appelées « grades »( code : wrv)

4°) elle peut se diviser en radian .

5°) la circonférence peut – être diviser en 100 parties égales

le cercle découpé ainsi est appelé diagramme circulaire ou « camembert » comme représentation graphique des pourcentages et en statistique .

6°) INFO 1

Longueur d’un ARC et d’une corde :

Info plus ++++

7°) INFO 2

Mesure d’un angle

Info plus +++

Pour mesurer un angle , on trace , avec un rayon quelconque , une circonférence ayant pour centre le sommet de l’angle et l’on mesure l’arc de cette circonférence compris entre les côtés de l’angle. La mesure de cet arc est la mesure de l’angle.

Dans la pratique , on opère cette mesure avec un rapporteur.

8°) INFO 3

Angle inscrit dans une demi circonférence .

Info plus ++++

On appelle « angle inscrit dans une demi- circonférence » , un angle dont le sommet est sur la circonférence et dont les côtés passent par les extrémités du diamètre.

Tous les angles ainsi inscrits mesurent 90°

9°) ,INFO 4

Le nombre « pi » : Ou rapport de la circonférence au diamètre .

Info plus +++

La longueur d’une circonférence quelconque divisée par la longueur de son diamètre donne toujours le même quotient :

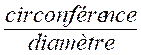= 3,14159…… , soit approximativement 3,1416

Ce nombre « 3,1416 » est le rapport de la circonférence à son diamètre. On le représente par la lettre grecque p ( prononcer « pi »)

10°) INFO 5

CALCULS de la longueur d’un arc

INFO PLUS ++++

>>Travaux auto – formatifs @

Quelle est la définition d’une circonférence ?

Quels sont les éléments d’une circonférence ?

(ils sont au nombres de .........)

Qu’appelle - t- on centre ?

Qu ‘appelle - t - on « cercle » ?

Qu ‘est ce que le « rayon » ?

Qu’est ce que le « diamètre » ?

Qu’est ce qu ‘une « circonférence » ?

Qu’est ce qu’un « disque » ?

A partir de quelle relation détermine - t- on la valeur de « pi » ? ( il y en a deux en fonction du diamètre et deux en fonction du rayon ).

Donner la formule qui permet de calculer le périmètre d’un disque :

a) en fonction du rayon.

b) en fonction du diamètre.

EVALUATION :

Niveau 1

1 ) Calculer la longueur du périmètre du disque de 10 cm de rayon.

2 ) Calculer la longueur du périmètre du disque de 10cm de diamètre.

Niveau 2 :

1 ) Calculer la longueur du rayon. du disque de périmètre : 628 mm

2 ) Calculer la longueur du diamètre du disque de périmètre égal à :628 mm.

3) Calculer le rayon d’un disque dont l’aire est de 1962.5 cm².

4 ) Calculer le diamètre d’un disque dont l’aire est de 3,14 m²

Problèmes :
1°) Le quart d’une circonférence mesure 20 cm .Quel est son diamètre ?

2°)