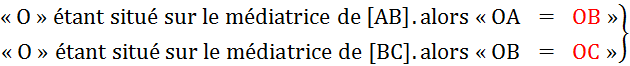Pré requis:

Retour vers le programme de 6^ème.	ICI le corrigé des travaux de 6^ème
droite et courbe : vue en primaire.
Notions préliminaires
Ligne droite (notion)		Classe de 5^ème (L2)

ENVIRONNEMENT du dossier:

Index « warmaths »

Info 1 : Liste des cours en géométrie. Info 2 : Tableau Info 3 : la géométrie en arithmétique

DOSSIER : ACTIVITES

Chapitres
Liste des 9 fiches :
Fiche 1	Série de constructions élémentaires (retour sur la classe de 6^ème )
Fiche 2	Droites parallèles ou perpendiculaires
Fiche 3	Distance de deux droites parallèles
Fiche 4	Les quadrilatères
Fiche 5	Positions relatives de deux cercles..
Fiche 6	DROITES et CERCLE
Fiche 7	DROITES REMARQUABLES DU TRIANGLE ( médianes ,médiatrices ,bissectrices, hauteurs ;.. cercle circonscrit )
Fiche 8
Fiche 9

Info COURS

FICHE 1 : Série de CONSTRUCTIONS ELEMENTAIRES.
	Construction élémentaire n°1
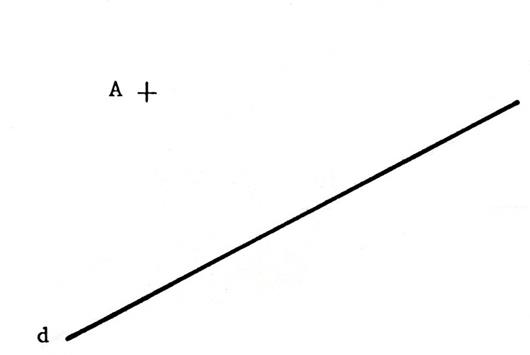
	Avec la règle et l’équerre , tracez par le point « A » la parallèle à la droite « d ».
	Construction élémentaire n°2
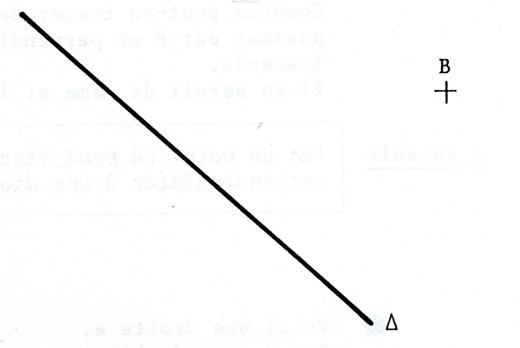
	Tracez en « B » la perpendiculaire à .
	Construction élémentaire n°3
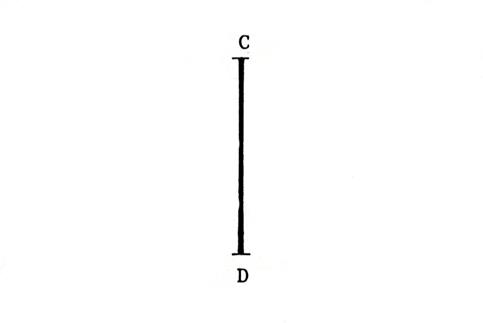
	En utilisant le compas et la règle , tracez la médiatrice à [ CD ]. (laissez les constructions).
	Construction élémentaire n°4
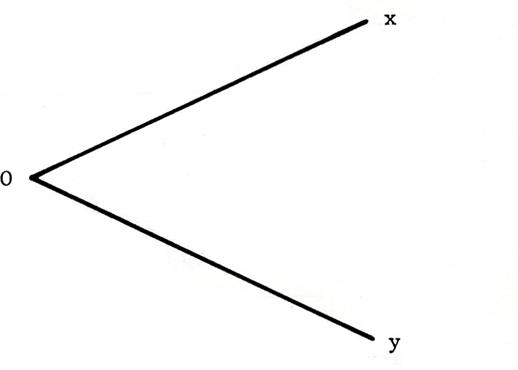
	En utilisant le compas et la règle , tracez la bissectrice de (laissez les constructions )
	Construction élémentaire n°5
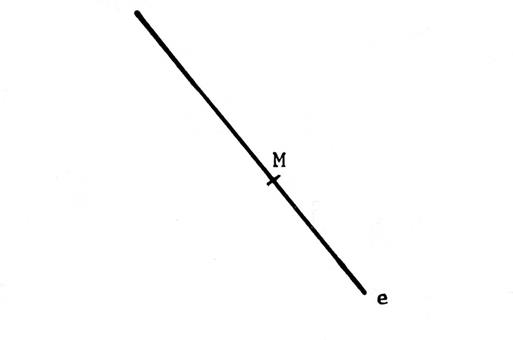
	En utilisant le compas et la règle , tracez par « M » la perpendiculaire à « e » (Laissez les constructions)
	Construction élémentaire n°6
	En utilisant le compas et la règle , tracez par « N » la perpendiculaire à « f » (Laissez les constructions)

	FICHE 2 : Droites parallèles ou perpendiculaires.				info 1 plus : les droites parallèles. ; Info 2 plus : les droites perpendiculaires.
	Activité 1 :
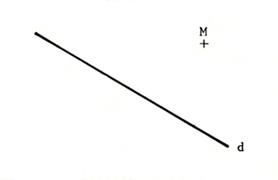
	Ci - contre on vous donne une droite « d » et un point « M ». Question : Combien peut-on tracer de droites passant par « M » et parallèle à « D » ? ……..Une seule droite.. Tracez cette droite …
	A retenir : Par un point pris hors d’une droite , on peut tracer une et seule droite à cette droite…
	Activité 2 :
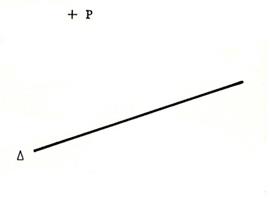
	Ci - contre on vous donne une droite «  » et un point « P ». Question : Combien peut-on tracer de droites passant par « P » et perpendiculaire à «  » ? ……..Une seule droite.. Tracez là … Remarque : Il en serait de même si le point « P » était sur la droite «  » ….
	A retenir : Par un point on peut tracer une et une seule perpendiculaire à une droite donnée.
	Activité 3 :
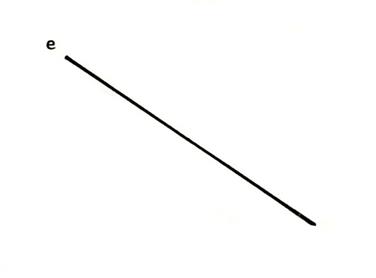
	Ci - contre on vous donne une droite « e ». Tracez deux droites , toutes, parallèles à « e ». Que pouvez-vous dire de ces deux droites ? ……elles sont parallèles entre –elles ……………………………….
	A retenir : Si deux droites sont parallèles à une même droite alors ces deux droites sont « parallèles ».
	Activité 4 :
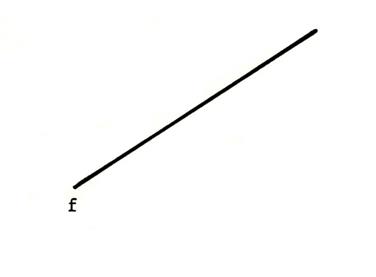
	Ci - contre on vous donne une droite « f ». Tracez deux droites, toutes, perpendiculaires à « f ». Que pouvez-vous dire de ces deux droites ? ……elles sont perpendiculaires entre –elles ……………………………….
	A retenir : Si deux droites sont perpendiculaires à une même droite alors ces deux droites sont « parallèles ».
	Activité 5 :
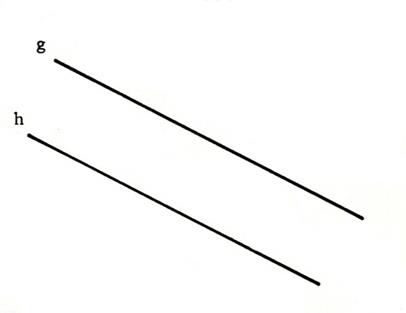
	Ci - contre on vous donne deux droites parallèles « g » et « h » . Tracez une droite « m » perpendiculaires à « g ». Que pouvez-vous dire de « m » et de « h » ? …… »m » est perpendiculaire à « h » ….
	A retenir : Si deux droites sont parallèles toute perpendiculaire à l’une est alors « perpendiculaire » à l’autre.
	FICHE 3 : Distance de deux droites parallèles.
	Activités 1
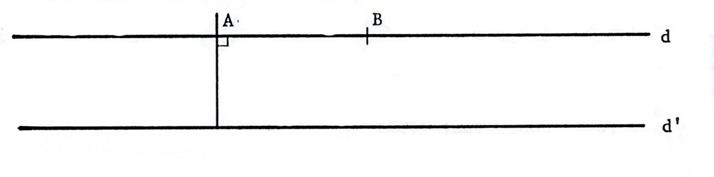
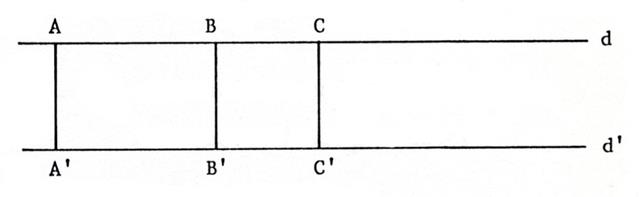
	Soient deux droites « d » et « d’ » parallèles. (voir ci- dessous). "A" est un point appartenant à « d ». On a tracé par « A » la perpendiculaire à « d » qui coupe « d’ » en « A’ ». Placez la lettre « A’ ». On peut affirmer (voir fiche 2) que ( A A’ ) est ..perpendiculaire …à la droite « d’ ».
	Soit « B » un autre point sur « d ». Tracez par « B » la perpendiculaire à « d » qui coupe « d’ » en « B’ ». Comme précédemment, vous pouvez affirmer que « B B ‘ » est ..perpendiculaire……………. à « d’ » . Considérons le quadrilatère «  A B B’ A’ ». D’après ce que l’on vient de dire , il a ses côtés consécutifs ………perpendiculaires…………. On peut donc affirmer que «  A B B’ A’ » est un ..rectangle… » (vu en 6^ème ). Puisque dans tout rectangle les côtés opposés ont même .Longueur.. , alors «  AA’ …= ….BB’ » En prenant n’importe quel point sur « d » ou « d’ » on trouverait toujours la même longueur. La mesure de cette longueur est appelée la distance des deux parallèles.
	Activité 2 :
	Ci-contre on vous donne deux droites parallèles « e » et « f ». Tracez un segment mettant en évidence la distance de ces deux parallèles. Mesurez cette distance ( en mm). Vous trouvez ………………..
	Activité 3 :
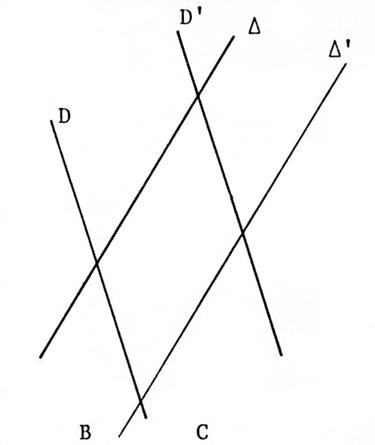
	Reprendre les consignes ci-dessus. Et Faites de même pour les droites « D » et « D’ » puis pour «  » et «  ‘». 1°) Donnez la distance de « D » à « D’ » = ………………….mm 2°) Donnez la distance de «  » à «  ‘» = ………………..mm.
	Activité 4 :
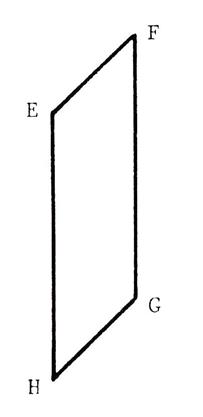
	Ci-contre on vous donne un parallélogramme « EFGH ». Vous savez que dans tout parallélogramme les côtés opposés sont …..parallèles ….. « HAUTEUR » On appelle « hauteur » du parallélogramme la distance de deux côtés opposés parallèles . Déterminez la valeur des deux hauteurs ( en mm) . « h 1 = ………………… » et «  h2 = ………………………. »
	Activité 5 : Axe médian.
	En reprenant la figure de l’activité 1 , on a placé les points « M », »N », « P » milieux respectifs des segments : [ A A ‘] , [B B’ ] et [C C’] . · Question : que constatez-vous pour ces points ?.....ils semblent alignés . · Tracez en rouge la droite passant par ces points. ( nous l’appelons « m ») Vous constatez que « m » est ……parallèle ………….. à « d » et « d’ ». Il en serait de même en plaçant « A », « B » et « C » n’importe où sur « d ».
	· Choisissez un point « R » quelconque sur « m ». · Tracez par « R » la perpendiculaire à « m » , ( elle est aussi …parallèle ….à « d » et « d’ »., elle coupe « d » en « H » et « d’ » en « H’ ». · Vous constatez que « R » est le .milieu… de [ H H ‘]
	On retiendra que la droite « m » est appelée « axe médian » des parallèles « d » et « d’ ».
	FICHE 4 : Les quadrilatères.					Info sur les quadrilatères.
	Activité 1
	Consignes : 1. Dessinez le rectangle « ABCD » dont on donne le côté [ AB ] et tel que la longueur du côté [ BC ] soit la moitié de la longueur du côté [ A B ]. 2. Tracez les diagonales [AC] et [ B D] . (Elles se coupent en « O ») 3. Tracez les axes de symétries de ce rectangle. ( ils coupent respectivement « ( AB ) » en « M » ; « (B C) » en « N » , « (CD) » en « P » , « ( DA ) » en « R »). 4. Tracez les segments , [MN] et [ NP], [PR] et [ RM]
	Activité 2
	Après les tracés effectués, on vous demande de répondre aux questions suivantes :
	I ) Nommez les points qui sont les milieux d’un ou de plusieurs segments. ( exemple : « M » est le milieu de [AB] )
	II ) En utilisant uniquement les points « A » , « B » , « C », « D » , « M » , «N » , « 0 », « P » ,  « R » , identifiez sur la figure :
	1°) Les droites qui sont (ou qui semblent ) parallèles. ( vous écrirez : par exemple : ( A B ) // ( C D )
	2°) Les droites qui sont perpendiculaires ( vous écrirez par exemple : ( AB ) ⏊ ( BC )
	3°) Les rectangles :
	4°) Les carrés :
	5°) Les losanges :
	6°) les parallélogrammes ( qui ne sont (ni carré) , ni rectangle , ni losange )
	7°) Les trapèzes rectangles.
	8°) les trapèzes quelconques.
	9°) Les triangles rectangles.
	10°) les triangles isocèles :
	FICHE 5: Positions relatives de deux cercles..					Info + : positions des cercles ..
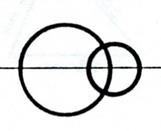
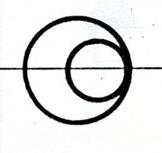
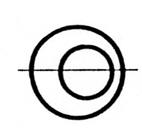
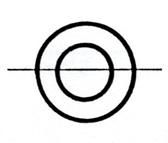
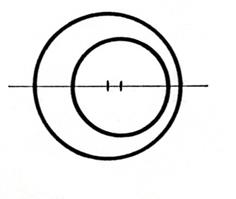
	Deux cercles occupent diverses positions l’un par rapport à l’autre. Activité 1 . Voici ; ci-dessous toutes les positions possibles. a) « cercles concentriques » , « cercles tangents intérieurement » ; « cercles sécants » ; « cercles tangents extérieurement » ; « cercles extérieurs » ; « cercles non-concentriques ». b) Précisez le nombre de points communs ? Pour chacune exemples proposés ci-dessous nommez chaque cas .
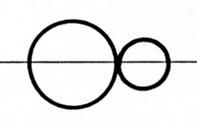
	Titre : Point commun :	Titre : Point commun : « cercles tangents extérieurement »							Titre : Point commun : « cercles sécants »
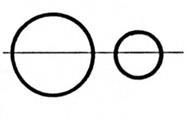
	« cercles extérieurs »
	Titre : Point commun : « cercles tangents intérieurement »	Titre : Point commun : « cercles non-concentriques »							Titre : Point commun : « cercles concentriques »
	Activité 2 :
	Dans chacune des cases, dessinez la position correspondant au titre. Placez les centres des cercles sur la droite déjà tracée (Marquez-les). Prenez pour rayon : R = 17 mm ; r = 10 mm. Indiquez le nombre de points communs.
	Exemple : Titre :Cercle à l’intérieur de l’autre (non concentrique) Point commun :…aucun ( 0 )	« cercles extérieurs »							« cercles tangents extérieurement
	« cercles sécants	« cercles tangents intérieurement »							« cercles concentriques »
	FICHE 6 : DROITES et CERCLE						Info +++ : le cercle et la droite..
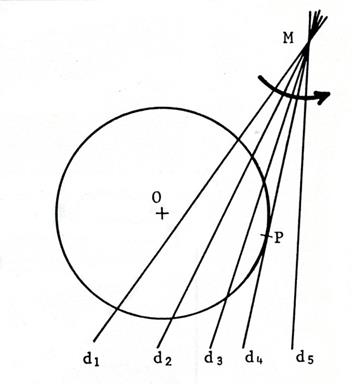
	Soit un point « M » sur une droite « d ». Imaginez cette droite tournant autour du point « M ». Elle occupe successivement les positions « d1 » , « d2 » , « d3 », « d4 », « d5 ». · Dans le cas des droites « d1 » , « d2 » , « d3 », la droite et le cercle ont deux points communs. · La droite continuant à tourner autour de « M », il arrive un moment où les deux points se cofondent en un seul : le point « P ». C’est le cas de la droite « d4 », On dit que la droite est tangente au cercle . Activité : tracez le rayon | O P] Question : Que pouvez – vous dire des droites ( M P ) et ( O P ) ? Réponse ………………les deux droites sont perpendiculaires…..
	A retenir : · Une tangente à un cercle est une droite qui n’a qu’un point commun avec ce cercle. · Elle est « perpendiculaire » au support du rayon passant par ce point.

FICHE 7 : CONSTRUCTION DE TRIANGLES.	Info + : info sur les triangles.
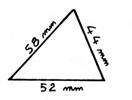
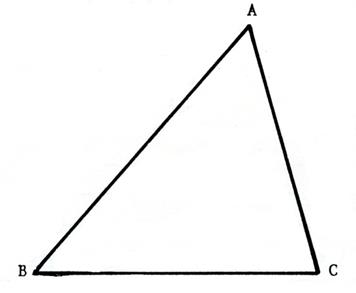
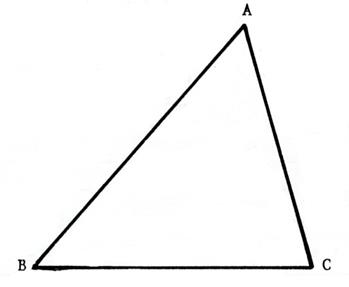
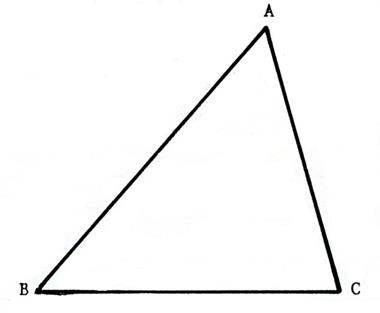
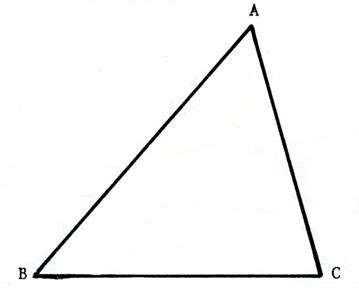
Activité 1 : Reproduisez en vraie grandeur , le triangle (scalène) dessiné ci-dessous.	Activité 2 : Reproduisez en vraie grandeur le triangle ci-dessous….
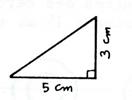
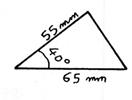
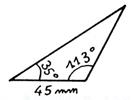
Activité 3 : Reproduisez en vraie grandeur le triangle rectangle ci-dessous.	Activité 4 : Reproduisez en vraie grandeur le triangle ci-dessous. (info + :triangle et angles)
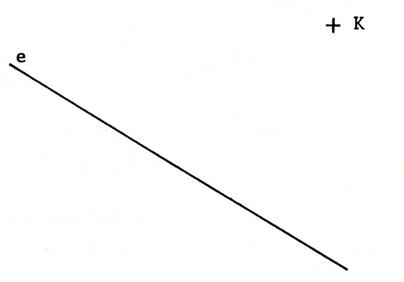
Activité 5 : Dessinez le triangle isocèle « KLM » dont la base est portée par la droite « e » et tel que « KL = 42 mm »	Activité 6 : Dessinez un triangle équilatéral dont la longueur du côté est de 50 mm.
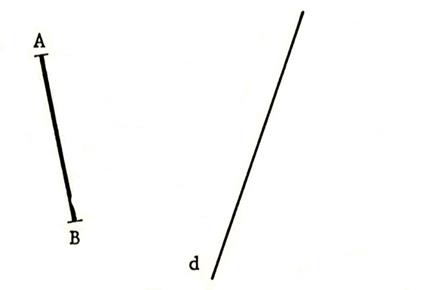
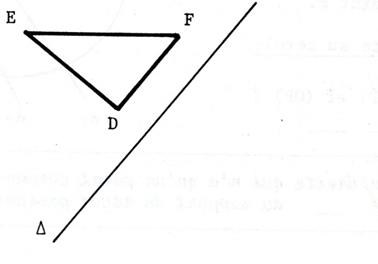
Activité 7 : Déterminez un point « D » sur la droite « d » tel que le triangle « ABD » soit isocèle de base [AB ] , laissez les traces de constructions.	Activité 8 : Dessinez le symétrique du triangle « DEF » par rapport à la droite «  ». ( voir symétrie centrale ou orthogonale)

FICHE 7 : DROITES REMARQUABLES DU TRIANGLE..		Info + : les droites remarquables et points particuliers dans un triangle.
Pour chaque cas :
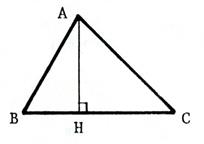
	Hauteur : [ A H ] Dites ce que le mot « hauteur » signifie dans le triangle.		Bissectrice  : [ A x ) Dites ce que le mot « bissectrice  » signifie dans le triangle.
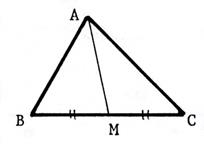
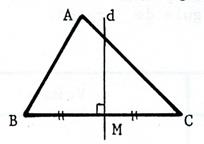
	Médiane : [ A M ] Dites ce que le mot « médiane  » signifie dans le triangle.		Médiatrice : ( d ) passant par « M » Dites ce que le mot « médiatrice » signifie dans le triangle.
Remarque : Dans tout triangle, il y a 3 médiatrices , 3 hauteurs , trois médianes , 3 bissectrices .
Activités : Sur chacun des triangles donnez ci-dessous, on vous demande de faire ces constructions ; Attention : · le tracé doit être fin , net , précis. · Dans chacun des 4 cas , les droites (ou portion de droites , ou segments) que vous allez tracé , doivent se couper en un même point. · Refaire le dessin si cela n’est pas le cas.
Dessinez les hauteurs :		Dessinez les bissectrices :
Dessinez les médianes :		Dessinez les médiatrices :
Remarques concernant les tracés des médiatrices :		Voir résumé sur le centre du cercle circonscrit dans un triangle..
Nous appelons « O » le point d’intersection de la médiatrice de [B C] et de celle de [A B]. donc OA = OB = OC
1^ère conséquence : « O » est situé aussi sur la médiatrice [A B]. 2^ème conséquence :

TRAVAUX AUTO FORMATIFS ( voir ci-dessus )

CONTROLE :

1) voir les «  à retenir » à réciter ………………..

EVALUATION

Faire tous les travaux dans la fiche……….