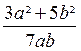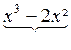|
|
|
|
|
|
|
|
|
|
|
ENVIRONNEMENT du dossier:
|
|
1°)
Résumé sur les priorités de calculs |
|
Info Géné.
|
|
|
|
|
RESUME sur
Calcul ALGEBRIQUE:
Dans ce résumé nous nous bornerons à rappeler les
définitions et les résultats vus dans les classes précédentes en complétant
l’étude des produits remarquables et
celle des fractions rationnelles.
|
EXPRESSIONS
LITTERALES : définitions ,valeur numérique,expressions
littérales équivalentes, calcul algébrique, opérations sur les expressions
littérales. |
@ |
|
|
@ info+ |
MONOMES : définition, monômes semblables, somme de monômes, différences
de monômes, produits de monômes,quotient de deux
monômes. |
@ info+ |
|
@ info+ |
POLYNOMES :définitions, degré,polynôme ordonné,polynôme homogène,polynômes
opposés, différence de deux polynômes,produit d’un polynôme par un
monôme,quotient de deux polynôme. |
@ info+ |
|
@ info+ |
PRODUITS ( ou IDENTITES) REMARQUABLES. Définition, (a+b)² ; ( a-
b)² ,Généralisation sur le carré d’un polynôme, ( a + b ) 3, ( a -
b ) 3, (a + b ) ( a - b), (
a3 - b3), ( a3 + b3), résumé , |
@ info+ |
|
@ info+ |
|
|
|
@ info+ |
Les fractions
rationnelles : Définition , simplification , réduction au
même dénominateur. |
@ info+ |
|
TEST |
COURS |
Interdisciplinarité |
|
CHAPITRE 1 :
|
@ |
Définition :
Une expression littérale est
l’indication de calculs à effectuer, ces calculs étant indiqués à l’aide de
lettres, de nombres et de signes opératoires.
Une expression littérale est aussi
appelée « expression algébrique ».
Exemples :
|
A = 3 a² + 2 b² |
B= 2 |
C = |
Si une expression renferme des
radicaux portant sur des lettres elle est irrationnelle, sinon elle
est rationnelle.
Valeur numérique.
On appelle « valeur numérique » d’une expression littérale pour
certaines valeurs attribuées aux lettres le nombre obtenu en remplaçant les
différentes lettres par les valeurs données et en effectuant les calculs qui
n’étaient qu’indiqués.
Ainsi la valeur numérique de
l’expression : 7 a² b3 + 5 ab² ; pour « a = -1»
et « b = -2 » est « - 56 -20 » = « -76 »
Expressions littérales équivalentes.
On dit que deux expressions
littérales sont équivalentes
lorsqu’elles prennent toujours la même valeur quelles que soient les
valeurs attribuées aux lettres.
Calcul algébrique .
Le calcul algébrique a pour but la transformation des expressions littérales en
expressions équivalentes.
Opérations sur les expressions
littérales :
Soient « A » et
« B »deux expressions littérales ;
Il est évident que
, quelles que soient les valeurs attribuées aux lettres qui entrent dans
« A » et « B » , la valeur numérique de l’expression
« A + B » est la somme des
valeurs numériques A et de B .
C’est pourquoi on dit que
l’expression « A + B » est la somme des expressions A et B.
De même, les expressions « A
- B » ; « A ×
B » et « ![]() » sont respectivement appelées « différence » , « produit » et « quotient » des
expressions « A » et « B ».
» sont respectivement appelées « différence » , « produit » et « quotient » des
expressions « A » et « B ».
Les opérations sur les expressions
littérales se feront en utilisant les propriétés des opérations sur les
expressions numériques puisque celles - ci sont applicables quelles que soient
les valeurs attribuées aux lettres.
Ainsi on peut écrire :3 a² b3 × 5 a6 b² = 15 ( a² × a 6
) × ( b3 × b² ) = 15 a8
b5
|
@ |
Définition.
Un monôme est une expression algébrique dans laquelle les seules opérations à
effectuer sur les lettres sont des multiplications. ( Ou
des élévations à une puissance qui sont des multiplications particulières).
Exemple : A = 3 × a² × b5
× a4×![]() × b²
× b²
Peut s’écrire : A = ![]() a6 b 8
a6 b 8
On dit alors que « A »
est écrit sous la « forme réduite ».
et ![]() est appelée « coefficient
numérique » et « a6 b 8 »
est appelée « partie littérale ».
est appelée « coefficient
numérique » et « a6 b 8 »
est appelée « partie littérale ».
MONOMES SEMBLABLES :
Deux monômes semblables sont deux monômes qui ont la même partie
littérale.
Exemple : 2 a3 b4 et -5
a3 b4
MONOMES OPPOSES :
Deux monômes opposés sont deux
monômes semblables qui ont des coefficients numériques opposés.
Exemple : 6 a² b3 et - 6
a² b3
DEGRE d’UN MONOME :
Le degré d’un monôme par rapport à
une de ses lettres est l’exposant de cette lettre dans le monôme.
Le degré d’un monôme ( ou degré par rapport à l’ensemble de ses lettres) est la
somme des degrés par rapport aux différentes lettres .
SOMME DE MONOMES :
La somme de plusieurs monômes
s’obtient en les écrivant à la suite les uns des autres et en les séparant par
le signe + , puis en associant les monômes semblables
s’il y a lieu.
Exemple: A = 2 a3 b²; B = 6 a3
b4 ; C = - 6 a5b2
; D = 5 a3 b²
A + B + C + D = 2 a3 b² + 6 a3 b4
+ - 6 a5b2 + 5 a3 b²
= 7 a3 b² + 6 a3 b4
+ - 6 a5b2
DIFFERENCE DE DEUX MONOMES
.Pour retrancher un monôme « B » d’un monôme « A » on peut
ajouter à « A » le monôme « B ».
Exemple :
A = 2 a3 b² ; B = - 6 a3
b4
A - B = 2 a3
b² + 6 a3 b4
Il en résulte la possibilité
d’écrire plus simplement la somme de plusieurs monômes dont certains ont des
coefficients numériques négatifs. Ainsi la somme des monômes A + B + C + D = 7 a3 b² + 6 a3 b4 - 6 a5b2
PRODUIT DE MONOMES.
Le produit de plusieurs monômes est le monôme qui a pour coefficient numérique
le produit des coefficients numériques et dont la partie littérale s’obtient en
prenant des lettres qui entrent dans les différents monômes et en affectant
chacune d’elles d’un exposant égal à la somme des exposants qu’
a cette lettre dans les différents monômes.
Exemple : A = 3
a²b3 ; B = 5ab4c² ; C = - 2 a3 b c4
A
B C = - 30 a 6 b8 c
6
QUOTIENT DE DEUX MONOMES:
Le quotient de deux monômes est la fraction quia pour numérateur le
dividende et pour dénominateur le diviseur.
On simplifie cette fraction, si cel est possible, comme une fraction numérique.
Exemple : A = 18 a² b8 ; B = - 12 a 4 b 6
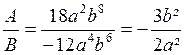
|
@ |
@ |
DEFINITIONS :
Un
polynôme est une somme algébrique de
monômes.
Un polynôme est à une ou
plusieurs variables suivant que les différents monômes qui le composent renferment
une ou plusieurs lettres.
On peut associer les monômes
semblables ; on dit alors qu’on « réduit » les termes
semblables.
Tout polynôme peut être considéré
comme une somme de monômes. Ces différents monômes sont les termes du polynôme.
Un polynôme réduit qui a deux
termes est un binôme et un polynôme réduit qui a trois termes est un trinôme.
DEGRE.
Le degré d’un polynôme par
rapport à une lettre est le plus fort exposant de cette lettre
dans le polynôme.
Le degré d’un polynôme est le degré
de celui de ses monômes qui a le plus fort degré .
POLYNOME ORDONNE.
Un polynôme est ordonné suivant les
puissances décroissantes d’une lettre lorsqu ‘en allant du premier monôme au dernier l’exposant de cette
lettre va constamment en diminuant.
Si cette exposant va constamment en
augmentant, on dit que le polynôme est ordonné suivant les puissances
croissantes de cette lettre.
On doit toujours ordonner les
polynômes afin de faciliter les opérations.
Lorsque ,
ayant ordonné un polynôme à une variable, il manque des termes d’un certain
degré, on dit que le polynôme est « incomplet ».
POLYNOME HOMOGENE :
On dit qu’un polynôme est homogène
lorsque tous ses termes ont le même degré.
Exemple : 3 a²b5 + 6 a b6
- 9 b7
POLYNOME OPPOSES :
Deux polynômes opposés sont deux polynômes
dont les termes sont deux à deux opposés.
Exemples : 3 a4 + 5 a² - 7
et - 3 a4 - 5 a² + 7
SOMME DE POLYNOMES.
Pour faire la somme de plusieurs polynômes on fait la somme des différents
monômes qui les composent et on réduit
les termes semblables s’il y a lieu.
Exemples :
A = 3 x3 + 6 x² + 4 x
- 1
B = 2 x 3 + 2x + 3
C = x 3 - 5 x² + 3
A
+ B + C = 6 x3 + x² + 6 x + 5
DIFFERENCE
DE DEUX POLYNOMES.
Pour retrancher un polynôme
« B » d’un polynôme
« A » on ajoute a « A » le
polynôme opposé de « B ».
Exemples :
A = 3 x3 + 4 x² - 6 x - 1
B = 2 x 3 - 6x² +7
A - B = 3 x3 + 4 x² - 6 x - 1 -2
x 3 + 6x² -7
A - B
= x3 + 10x² -6 x -8
ADDITION ET SOUSTRACTION
DE POLYNOMES.
Une
suite d’additions et de soustractions de polynômes doit se transformer
ou se ramener à une somme algébrique de
polynômes.
Exemple :
soient les polynômes :
|
A |
= |
6 x4 |
+ |
3 x3 |
- |
5 x² |
+ |
4x |
- |
1 |
|
B |
= |
- 5x4 |
+ |
3 x² |
|
|
|
|
+ |
7 |
|
C |
= |
- 3 x4 |
- |
6x3 |
|
|
+ |
4x |
- |
8 |
|
D |
= |
- 6 x4 |
- |
4 x3 |
- |
8 x² |
- |
5x |
|
|
Calculer A - B + C - D
|
A |
= |
6 x4 |
+ |
3 x3 |
- |
5 x² |
+ |
4x |
- |
1 |
|
- B |
= |
5x4 |
|
|
- |
3 x² |
|
|
- |
7 |
|
C |
= |
- 3 x4 |
- |
6x3 |
|
|
+ |
4x |
- |
8 |
|
- D |
= |
6 x4 |
+ |
4 x3 |
+ |
8 x² |
+ |
5x |
|
|
|
A
- B +C - D |
= |
1 4 x² |
+ |
x3 |
- |
10 x² |
+ |
13x |
- |
16 |
PRODUIT D’UN POLYNOME PAR UN MONOME.
Pour multiplier un polynôme par un
monôme on multiplie chaque terme du
polynôme par le monôme et on ajoute les résultats obtenus.
Exemple : A = 3 x² + 5 x - 1
B = 3 x 3
AB = 9 x5 + 14 x 4
- 3 x3
PRODUIT DE DEUX POLYNOMES.
Pour faire le produit de deux
polynômes on multiplie chaque terme du premier polynôme par chaque terme du
second et on ajoute les résultats obtenus.
Si les deux polynômes sont
compliqués, il est commode de disposer l’opération en écrivant les monômes
semblables des différents produits partiels les uns au - dessous des autres.
Exemple :
A = 2x² +
3 x y - y²
B = x² -
2 x y + 3 y²
|
2 x² |
+ 3 xy |
- y² |
|
|
|
x² |
- 2xy |
3y² |
|
|
|
2 x4 |
+ 3 x3 y |
- x² y² |
|
|
|
|
- 4 x 3 y |
- 6 x² y² |
+ 2 x y3 |
|
|
|
|
6 x² y² |
+ 9 x y3 |
- 3 y4 |
|
2x4 |
- x3 y |
- x² y² |
+ 11 x y3 |
-3 y4 |
QUOTIENT DE DEUX POLYNOMES
.
Le quotient de deux polynômes est
la fraction qui a pour numérateur le polynôme dividende et pour
dénominateur le polynôme diviseur.
Nous verrons plus loin qu’il est
parfois possible d’écrire ce résultat
plus simplement.
|
@ |
PRODUITS REMARQUABLES ou IDENTITES REMARQUABLES. |
On appelle « produits
remarquables » les résultats de certaines multiplications qu’on doit
savoir par cœur parce qu’ils permettent d’effectuer plus rapidement des
transformations d’expressions littérales. Les égalités auxquelles on est
conduit sont appelées « identités ».
|
1°)
( a + b ) ² |
@ |
On a :
(
a + b ) ² = ( a + b ) ( a + b )
=
a ² + b a + a b + b²
= a ² + 2 a b + b²
(
a + b ) ² = a ² + 2 a b + b²
|
2°)
( a - b ) ² |
@ |
On pourrait comme précédemment
effectuer la multiplication ( a - b) ( a - b) , mais
il est plus simple de déduire le résultat du précédent.
En effet on peut écrire :
( a - b ) ²
= [ a + (-b)]²
= a ² +(- b) a + a (-b) +(- b)²
= a ² +
2 a ( -b) + (- b)²
= a² -
2ab + b²
(
a - b ) ² = a² -
2ab + b²
On dit qu’on a déduit ce résultat
du précédent en “changeant “b” par
“-b”.
|
@ |
GENERALISATION. CARRE D’UN
POLYNOME. |
@ |
( on
utilise pour la démonstration appelée : méthode par récurrence)
Considérons d’abord un polynôme de
3 termes a + b + c . On peut calculer ( a+ b+ c) ² en considérant « a+ b + c» comme
étant la somme de deux termes : « a+b » et « c » . On
obtient ainsi :
|
|
( a+ b+ c) ² = (a + b) ² + 2 ( a + b) c + c² = a² + 2ab + b² + 2ac + 2 bc + c² = a² + b² + c² + 2ab + 2ac + 2bc |
|
On voit que le résultat trouvé est égal à la somme des carrés de tous les termes augmentée de la somme de tous les doubles produits de
ceux - ci pris deux à deux comme dans le cas du carré de la somme de deux termes.
Voyons si cette règle est générale . Pour cela admettons qu’elle est vraie dans le cas
de « n » termes « a ; b ; c ; ……k ; l »
et voyons si elle est vraie lorsqu’il y a un terme de plus « m »
Admettons donc que l’on a :
(a +
b + c + ……+k + l )² = a² + b² + c² + ……….+ k²+ l² + 2ab + 2ac + ………2 k l
et calculons (a + b + c + ……+k +
l + m )² en considérant « a + b +c + …..k + l+ m » comme
la somme de deux termes :
« a+ b + c +……..k + l »
et « m »
On
a :
(a +
b + c + ……+k + l +
m )² = (a + b +
c + ……+k + l )²+ 2 (a+ b + c +……..k + l )m + m²
Si on développe le carré et le
double produit ,
1°) Les carrés de a ; b ;
c ; … k ; l sont dans le
développement du carré et « m² » est dans le dernier terme,
2°) tous les doubles produits qui
ne contiennent pas « m » sont dans le développement du carré et tous
ceux qui contiennent « m » sont dans le deuxième terme.
D’autre part ,
il n’y a pas d’autres termes que ces carrés et ces doubles produits.
Finalement on voit que le résultat
obtenu est la somme des carrés de tous les termes augmentée de la somme de tous
les doubles produits.
La règle est vraie pour « n =
2 » il en résulte qu’elle est vraie pour « n+1 = 3 ». Etant
vraie pour « n = 3 » elle est vraie pour « n+1 = 4 ».
En
procédant de proche en proche on voit qu’elle est vraie quel que soit le
nombre de termes.
( a + b + c + …..+ k + l + m )² = ![]() +
+ ![]()
Nota : pour le symbole
![]() lire « la somme des… »
lire « la somme des… »
Pratiquement ,
afin de n’oublier aucun double produit, on écrit les doubles produits de chaque
terme par tous ceux qui le suivent.
Exemple :
Soit à calculer A = ( 3 x3
+ 4 x² - 5 x - 3)²
On
a A
= 9 x6 + 16 x 4
+ 25 x² + 9 + 24 x5 - 30 x4 - 18 x3 - 40 x3
- 24 x² + 30x
=
9 x6 + 24 x5 - 14 x4 - 58 x3 + x ² + 30 x + 9
REMARQUE
: la méthode employée dans la démonstration précédente est appelée”Méthode par
« récurrence » . On voit en quoi elle consiste :
Ayant remarqué que la propriété est vraie pour les premières valeurs de
« n » on suppose qu’elle est vraie pour une valeur de « n »
quelconque et on démontre qu’elle est vraie pour « n+1 ». Etant vraie
pour « n = 2 » ; n= 3 , ….elle est générale.
|
|
( a + b ) 3 |
|
On a ( a + b )3 = ( a + b ) ² ( a + b)
= ( a² + 2a b + b² )
( a + b)
= a 3 + 2a²
b + b² a + a² b + 2 ab² + b 3
= a 3 + 3 a² b + 3 ab²
+ b3
( a + b )3 = a 3
+ 3 a² b + 3 ab² + b3
On écrit parfois ce résultat sous
la forme :
( a + b )3 = a
3 + b 3 + 3 a b (
a + b)
|
|
( a - b ) 3 |
|
Changeons les résultants précédents
“b” en “-b” . On obtient :
( a - b )3 = a 3
- 3 a² b + 3 ab² - b3
( a - b )3 = a 3
- b 3 + 3 a b ( a -
b)
|
( a + b ) ( a - b) |
|
Effectuons la multiplication.
On a : ( a + b ) ( a - b) = a² +
b a - a b - b²
= a² - b²
( a + b ) (
a - b) =
a² - b²
|
@ info |
a3 -
b 3 |
|
Nous avons déjà trouvé :
( a - b )3 = a 3 - b 3 + 3 a b ( a -
b)
On
en déduit :
a 3 - b 3 = ( a - b) 3 + 3 ab ( a -
b)
= ( a - b ) [ ( a - b )
² + 3 a b ]
= ( a - b ) [ ( a² -
2ab + b² + 3 a b ]
= ( a - b) ( a ² + a b + b² )
a 3 - b 3 =
= ( a - b) ( a ² + a b + b² )
|
@ info |
a3 +
b 3 |
|
Changeons dans
le résultat précédent “b” par “-b”
On
obtient: a3
+ b 3
= ( a + b ) ( a² - a b + b²)
En résumé,
on doit savoir par Coeur les résultats
suivants :
|
|
( a + b ) ² = a² + 2 a b + b² ( a - b ) ² = a ² - 2 ab + b² ( a + b ) ( a - b) =
a² - b² On se rappel era des calculs
suivants: ( a + b + ….+ m )² = ( a + b )3 = a 3 + 3 a² b + 3 ab²
+ b3 = a 3 + b 3 + 3 a b ( a + b) ( a - b )3 = a 3 - 3 a² b + 3 ab²
- b3 = a 3 - b 3 + 3 a b ( a - b) a 3 - b 3 =
= ( a - b) ( a ² + a b + b² ) a3 + b
3 = ( a + b ) ( a² - a
b + b²) |
|
REMARQUE
: Les polynômes qui sont dans les deux membres de chacune des identités
précédents sont “homogènes” et du même degré .
|
@ |
1ère
APPLICATION : La factorisation
d’un polynôme du second degré : on regarde si deux termes ne sont pas le
début d’un développement de la
forme :
1°) a² + 2 a b
+ …….= qui se ramène à la
forme ( a + b)
² ou a² + 2……+ b² ) = ( a + b )²
2°) a² - 2 a b
+ …….= qui se ramène à la
forme ( a -
b) ² ou a² - 2……+ b² ) = ( a - b )²
3°) a²
- b² qui se ramène à la forme ( a + b ) ( a - b
)
2ère
APPLICATION Tout d’abord, les produits remarquables permettent de calculer « une
puissance d’un polynôme ».
Exemple 1 .
Calculer A = ( x
+ 2 y ) 4
On a : A = [ ( x + 2 y ) ² ]²
= ( x²
+ 4 x y + 4 y² ) ²
= x 4 + 16 x² y ² + 16 y ² + 8 x3 y + 8 x² y²
+ 32 x y 3
= x 4 + 8 x3 y + 24 x² y²
+ 32 x y 3 + 16 y 4
Exemple 2 .
Calculer B = ( x
+ y + 1 ) ²
On a : B = ( x + y ) 3 + 3 ( x + y ) ² + 3 ( x + y ) +1
= x3 + 3 x² y + 3 x y² + y 3 + 3 x² + 6 x y + 3
y² + 3 x + 3y + 1
3ème
APPLICATION : « l’identité »
( a + b ) ( a - b) =
a² - b²
permet d’obtenir
le produit de certains polynômes particuliers sans poser la multiplication.
Cela se produit si les deux
polynômes sont formés de nombres dont les uns sont les mêmes et les autres
opposés deux à deux.
|
Exemple 1 :Calculer l’expression : A = ( 2x
+ 5 y +1) ( 2x - 5y +1 ) |
Exemple 2 . Calculer l’expression : B = ( 2x
+ 5 y +1) ( 2x - 5 y -1) ² |
|
On a A
= ( 2x +1)² - ( 5 y)² = 4 x² + 4x + 1
- 25 y² |
On a B = ( 2x²)² - ( 5y
+1 )² = 4 x² - ( 25 y² +
10 y +1 ) =
4 x² - 25 y² - 10 y - 1 |
4ème APPLICATION .
Dans la suite du cours
, nous avons à mettre un polynôme sous la forme d’un produit de facteurs
. Ce problème n’est pas toujours possible. Nous ne nous proposons pas d ‘
examiner dans quels cas on peut le
résoudre mais simplement d’indiquer les essais que l’on doit faire pour essayer
d’obtenir le résultat demandé.
1°) On regarde si on peut mettre
une expression en facteur.
Exemples :
|
A = a b
+ a c - a d = a
( b + c - d) |
B = 6 x² y² + 9 x² y 4 = 3 x² y² ( 2x
+ 3 y²) |
|
C = 2 ( a + b ) ² + 3 ( a + b ) ²
= ( a + b )² [ 2 ( a + b) + 3 ]
= ( a + b )² ( 2a + 2 b + 3 ) |
D
= ( x + y ) ( x + 5 y ) - ( x + y ) ( 6x -
4y) = ( x + y ) [(
x + 5 y ) - ( 6x - 4y)] =
( x + y )
( x + 5 y - 6 x + 4 y) = ( x + y ) ( -
5 x + 9 y) |
2°) On remarque si l’expression
donnée est la différence des carrés de deux polynômes ( ou
monômes) et on utilise l’identité :
a² - b² = ( a + b ) ( a - b)
Exemples :
|
A = 9 x² - 16 y² = ( 3
x + 4 y ) ( 3 x - 4 y) |
B = a² + 4 ab + 4 b² - 1 = ( a + 2b ) ² - 1 = ( a + 2b + 1) ( a + 2b - 1
) |
C
= 4 x² - y ² - 4 x + 1
= ( 2x -
1 )² - y ²
= ( 2x -
1 + y ) ( 2 x - 1 - y )
3°)De même
, une expression pourra être mise sous
la forme d’un produit de facteurs si elle est la différence ou la somme de deux
cubes.
On utilisera alors les résultats
établis précédemment pour l’égalité «
a 3 - b 3 = ( a
- b) ( a ² + a b + b² ) » et
l’égalité « a3 +
b 3 = ( a + b ) ( a² - a b + b²) »
Exemple :
A = a 3 - 8 b6
=
( a - 2 b²) ( a² + 2a b + 4 b4)
4°) On regarde si une
transformation préalable de l’expression donnée permet d’obtenir une mise en
facteur.
Exemples :
A = a² -
4 b² + ( 2 a - 4 b)²
= (
a + 2 b ) ( a - 2 b) + 4 ( a - 2 b)²
= ( a - 2b )
[ ( a + 2 b ) + 4 ( a - 2 b)]
= ( a - 2b ) ( a + 2b + 4 a - 8 b)
=
( a - 2 b ) ( 5 a - 6 b)
B = x 3 ( x - z ) + y 3 ( z - z ) + z3 ( x - y
)
= x3 y - x 3z + y 3 z - y3 x
+ z3 ( x - y )
= ( x 3
y - y 3 x ) - ( x3 z - y3 z ) + z3 ( x - y)
= x y ( x² - y² ) - z ( x3 - y 3
)+ z3 ( x - y )
= x y ( ( x - y ) ( x + y ) - z (
x - y ) ( x² + x y + y² ) + z3 (
x - y )
= ( x - y ) [ x y ( x + y ) - z ( x² + x y + y²
) + z3 ]
Considérons maintenant l’expression
entre crochets.
On peut écrire :
x² y + x y² - z x² - x
y z - z y² + z²
= ( x²y
- z x ² ) + ( x y² - x y z ) - ( z y² - z3 )
= x² ( y - z ) + x y (
y - z ) - z ( y -z)( y + z)
= ( y
- z) [ x² + x y - z ( y + z ) ]
et B =
( x - y ) ( y - z ) [ x² + x y - z ( y +
z ) ]
La nouvelle expression entre
crochets peut s’écrire :
x ² + x y - z y - z²
=
( x² - z² ) + ( x y - z y)
= ( x + z ) (
x - z ) + y ( x - z)
=
( x - z ) ( x + y + z )
Finalement , de la
forme développée de B = x 3 ( x - z ) + y 3 ( z
- z ) + z3 ( x - y )
on a par transformation successive la forme « factorisée » :
B = ( x - y ) ( y - z ) ( x - z ) (
x - z ) ( x + y + z )
|
@ |
Définition. On appelle
« fraction rationnelle le quotient de deux monômes ou polynômes.
Exemples : 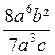 ;
; 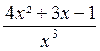 ;
; 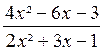
Le dividende est le numérateur de
la fraction, le diviseur est son dénominateur ;le
numérateur et le dénominateur en sont les deux termes.
|
SIMPLIFICATION. |
|
Le premier problème qui se pose est
évidemment d’écrire une fraction rationnelle sous la forme la plus simple,
c’est à dire de la simplifier.
Une fraction rationnelle sera d’autant
plus simple que ses deux termes seront de plus petit degré. De même que pour
une fraction numérique, pour simplifier une fraction rationnelle, on
divisera ses deux termes par un même
facteur.
Pour cela ,
on essaiera de mettre ses deux termes sous forme de « produits de
facteurs ». On pourra alors simplifier la fraction s’il y a au
numérateur et au dénominateur un facteur commun.
Exemples :
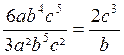 (
le produit de facteurs communs est : 3 a²b4c² )
(
le produit de facteurs communs est : 3 a²b4c² )
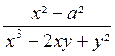 =
= 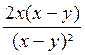 =
= 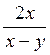 (
après factorisation on trouve le facteur commun (x-y)
(
après factorisation on trouve le facteur commun (x-y)
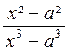 =
= 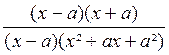 =
= 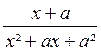
REMARQUE 1 :
Il faut bien faire attention de ne pas supprimer un
même terme au numérateur et au dénominateur si ceux-ci n’ont pas été mis sous
forme de produits.
Par exemple : il ne faut pas écrire : 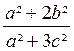 =
= ![]() en supprimant « a² » aux termes
car, en procédant ainsi, on retranche « a² » aux deux termes et on
n’obtient pas une fraction équivalente. ( pour
vérifier qu’il n’y a pas égalité donner par exemple à « a = +2» et « b= + 3» il suffit ensuite de
faire le calcul. Dans chaque membre)
en supprimant « a² » aux termes
car, en procédant ainsi, on retranche « a² » aux deux termes et on
n’obtient pas une fraction équivalente. ( pour
vérifier qu’il n’y a pas égalité donner par exemple à « a = +2» et « b= + 3» il suffit ensuite de
faire le calcul. Dans chaque membre)
REMARQUE 2 : Il arrive fréquemment qu’on peut
mettre immédiatement un des termes d’une fraction sous la forme d’un produit de
facteurs du premier degré de la forme (x -a
) ( x - ³ ) …….
Il est alors naturel de se demander s’il est
possible de mettre en facteur dans l’autre terme l’un des binômes (x -a
) ( x - ³ ) …….
*
Soit par exemple la fraction :
A
= 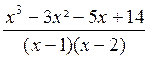
Examinons si dans le numérateur « N » on
peut mettre « x- 1 » en
facteur, c’est à dire s’il existe un polynôme « N’ » tel que l’on ait
quel que soit « x » :
N = ( x - 1) N’
S’il en est ainsi, pour « (x - 1 ) N’ = 0 »
donc « N = 0 »
Or pour « x = 1 ; N = 1 - 3 - 5
+14 ; donc dans « N » on ne peut certainement pas mettre
« x-1 » en facteur.
Voyons de même si dans « N » il est
possible de mettre « x-2 » en facteur.
Le même raisonnement que précédemment nous prouve
que pour qu’il en soit ainsi il faut que « N » s ‘ annule pour
« x = 2 »
Pour « x = 2 » ,
on a « N = 8 - 12 -10 +14 = 0
» donc dans « N » on peut peut - être
mettre « x - 2 » en facteur. Pour voir si cela est effectivement possible , nous allons essayer de mettre
« N » sous la forme d’une
somme de binômes dans lesquels on peut mettre « x-2 » en facteur .
Avec le
premier terme « x3 » il faudrait « -2x² » ;
on aurait ainsi « x 3 - 2 x²
= x² ( x
- 2) »
Comme dans « N » on a
« -3x² » (
et non pas « -2x²) il faut
ajouter « -x² »
Avec
« -x² » il faudrait « 2x » ,
on aurait ainsi : - x² + 2x = - x ( x - 2)
Comme dans « N » on a « -5x »
(et non pas « 2x ») il faut ajouter « -7 x »
Finalement il reste donc - 7 x + 14 = - 7 ( x -2)
Les calculs précédents se résument ainsi :
|
N = |
|
- |
- |
|
|
x²( x - 2) |
- x ( x -2) |
- 7 ( x +2) |
N = ( x - 2 ) ( x² - x - 7 )
Nous pouvons
donc simplifier la fraction « A » et écrire :
A = 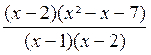 =
= 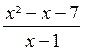
|
REDUCTION AU MEME DENOMINATEUR. |
|
On peut prendre pour dénominateur commun le produit
des dénominateurs.
Soient par exemple les deux fractions :
![]() et
et
![]()
La 1ère
est équivalente à 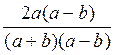 et la seconde à
et la seconde à 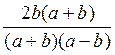
Il est souvent possible de trouver un dénominateur
commun plus simple que le produit des dénominateurs.
Pour qu’une
expression puisse être prise comme dénominateur
commun, il suffit qu’elle contienne en facteur chacun des dénominateurs des
différentes fractions.
On pourra former le dénominateur commun en
utilisant une règle analogue à celle
utilisée pour les fractions numériques : (
@ info) On décompose les dénominateurs eu
produits de facteurs et on fait le produit de tous les facteurs , communs ou
non communs , chacun d’eux étant pris avec son plus fort exposant .
EXEMPLE 1 : Réduire au même dénominateur :
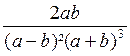 et
et 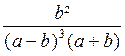
On pourra prendre comme dénominateur commun ( a + b ) 3
( a - b )3
Les deux fractions
données sont équivalentes à :
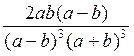 et
et 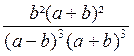
EXEMPLE 2 :
Réduire au même dénominateur :
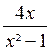 ;
; 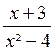 et
et 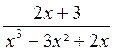
Mettons les dénominateurs sous forme de produits .
x² - 1 = ( x +1) ( x -
1)
x² - 4 = ( x +2) ( x -
2)
x3 - 3 x² + 2x = x ( x²
- 3x +2 )
Regardons si dans le trinôme « x² - 3x +
2 » on peut mettre en facteur l’un des facteurs des deux premiers
dénominateurs.
Pour
« x = 1 » ; on a
x² - 3x + 2 = 1 - 3 + 2 = 0
Donc ,
dans ce trinôme il est peut-être possible de mettre « x-1 » en
facteur.
En procédant comme nous l’avons vu pour A = 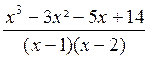 nous écrirons :
nous écrirons :
x² - 3 x + 2 = x² -x - 2x +2
= x ( x-1) - 2 ( x -1)
= ( x - 1 ) ( x - 2 )
Donc x3
- 3 x² + 2x = x ( x - 1) ( x - 2)
Finalement, on prendra pour dénominateur
commun « x (x-1)(x+1)(x-2)=
x ( x²-1) ( x² - 4) et les fractions données sont respectivement équivalentes à :
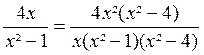
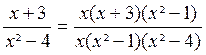
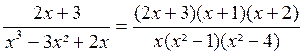
|
OPERATIONS . |
|
Les opérations sur les fractions rationnelles se font
en appliquant les mêmes règles que pour les fractions numériques.
Exemple 1 Calculer l’expression :
A = 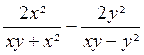
Les deux fractions se simplifient et on a :
A
= 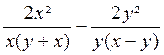
= 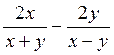
= 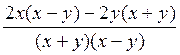
= 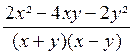
Exemple2 : Calculer
l’expression :
A =
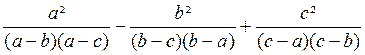
Nous prendrons pour dénominateur commun :
( a
- b) ( b - c) (c - a)
A
= 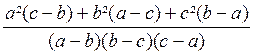
Regardons si le résultat obtenu peut se simplifier.
Pour voir si dans le numérateur « N » on peur mettre « a
-b » en facteur , remplaçons « a » par
« b » ; on obtient :
* b ² ( c -b) + b² ( b- c) + c² × 0 = 0
Dons dans « N » on peut « peut
être » mettre « a - b » en facteur .On a :
N = a² c
- a²b + b² a - b² c - c² ( a -b)
= c( a² - b² ) - a b ( a - b) -
c² ( a - b)
= c ( a- b)
( a + b )- a b ( a - b ) - c² ( a - b)
= ( a
- b) ( ac + b c - a b - c² )
Donc
A = 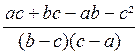
Pour b = c , le numérateur « N’ » s’annule .
Il est donc , peut - être
possible de mettre « b -c » en facteur dans « N’ ».On
a :
N’ = a (
c - b ) + c ( b - c)
= ( b - c ) ( c - a)
Finalement A = 1
Exemple 3 . Calculer l’expression :
A
= 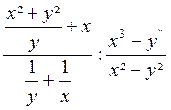
La 1ère fraction est égale à :
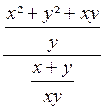 =
= 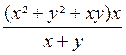
Donc A
= 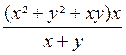
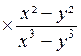
= 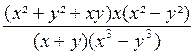
= 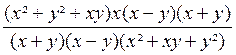
A = x
DEVOIR : Voir chapitre par chapitre.
Pour chaque chapitre , et
pour approfondir cliquer sur « @ info »
EVALUATION
Pour chaque chapitre, et pour approfondir cliquer
sur « @
info »