THALES

Auteur : WARME R.

MATHEMATIQUES :Niveau V.

THALES:

NOM : ………………………………

Prénom : …………………………..

Classe :…………………..

Année scolaire : ………………………

Dossier pris le : ……/………/………

Validation de la formation : O - N

Le : ……………………………………..

Nom du formateur : ……………………

ETABLISSEMENT : …………………………………………..

DOC. INFO : Professeur -Formateur

21 / 26

DOC : livre Elève .Cours interactifs - et travaux + corrigés.

TITRE : PROPRIETE de THALES.

DOSSIER N°21 COURS INTERACTIF

PROPRIETE de THALES.

Information « TRAVAUX d’auto - formation »

Cliquer sur le mot !.

INFORMATIONS PEDAGOGIQUES :

NIVEAU :

Formation Niveau V (inclus le CAP et CFA)

OBJECTIFS :

- savoir calculer la longueur d'un segment de droite en utilisant la propriété de Thalès.

I ) Pré requis:

Activités : divisions de segments

Lectures importantes :

Les proportions ;Calculs sur la proportionnalité.

Les pré requis sur les projections N°1

Les triangles semblables est homothétiques

II ) ENVIRONNEMENT du dossier :

Index

Objectif précédent :

1°) projection d’un segment.

2°) Cours : les proportionnalités.

2°)lire :Le théorème de Thalès

Objectif suivant :

1°)Cours BEP indus.

2°) programme : la trigonométrie .

1°)Tableau :

2°) Liste des cours ( formation CAP)

3°) Sommaire des cours sur Thalès.

III ) LECON n° 21: LA PROPRIETE de THALES.

Chapitres :

I ) Propriété de Thalès pour deux droites sécantes .

Cd :Info plus

II ) Propriété de Thalès pour un triangle .

Cd :Info 1 plus et Cd :Info 2 plus

III ) Utilisation de la propriété de Thalès .

Cd :Info plus

IV) INFORMATIONS « formation leçon » :

Test

COURS

Travaux auto - formation.

Corrigé des travaux auto - formation.

Contrôle

évaluation

1°) Cliquer ici : INTERDISCIPLINARITE .

2°)Application : le pantographe.

3°)divisions d’un segment en parties égales , sans règle graduées , ni calculs.

CORRIGE contrôle :

CORRIGE évaluation :

V ) DEVOIRS ( écrits):

Devoir : Evaluation basique (tout niveau)

Devoir diagnostique L tests.

Devoir Auto - formatif ( intégré au cours)

Devoir Formatif « Contrôle : savoir » ; ( remédiation)

Devoir Formatif « Evaluation savoir faire » ( remédiation)

Devoir sommatif .

Devoir certificatif : ( remédiation )

* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .

Leçon

Titre

N°21

PROPRIETE de THALES.

CHAPITRES :

I ) Propriété de Thalès pour deux droites sécantes .

Cd :Info plus

II ) Propriété de Thalès pour un triangle .

Cd :Info 1 plus et Cd :Info 2 plus

III ) Utilisation de la propriété de Thalès .

Cd :Info plus

COURS

I ) PROPRIETE de Thalès pour deux droites sécantes .

Cd :Info plus

Propriété de Thalès pour deux droites sécantes :

Des droites parallèles déterminent sur des droites sécantes des segments proportionnels :

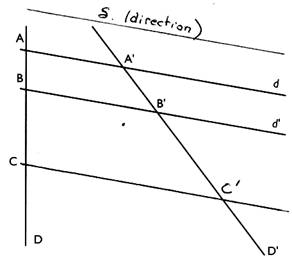
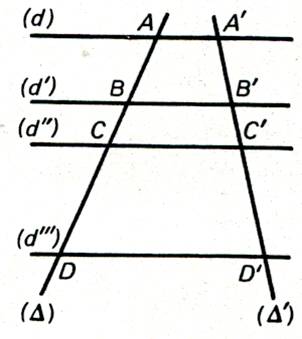
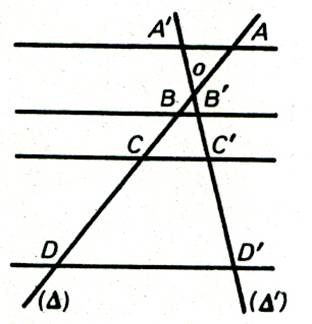
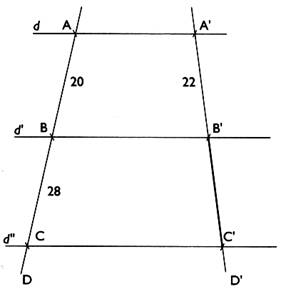
Voyons :

Sur la figure ci- dessous on a tracé trois droites , parallèles à la direction "delta" (symbole : d )coupant deux droites D et D' ( non parallèles ).

A à pour image A' ; B à pour image B' et C à pour image C' .

F Activités :

Nous considérons les segments sur D :

Mesurer A B = …… ; BC = ……….; AC = ……….

Nous considérons les segments sur D' :

Mesurer A' B' = …… ; B'C' = ……….; A' C ' = ……….

Il faut vérifier si les rapports suivants sont égaux :

Première vérification :

On calcule successivement chaque rapport :

A partir des relevés précédents :

Deuxième vérification :

on vérifie que les rapports suivants forment une suite de rapports égaux :

On calcule successivement chaque rapport : ( recherche de la valeur décimale)

A partir des relevés précédents :

Bilan : L ' égalité de ces rapports permet de prétendre que les segments [ A' B'] , [B' C'] et [ A' C' ] sont proportionnels aux segments [ A B] , [B C] et [ A C ] .

Ainsi la propriété de Thalès pour deux droites sécantes :

Des droites parallèles déterminent sur des droites sécantes des segments proportionnels :

II ) Propriété de Thalès pour un triangle .

Cd :Info plus

Propriété :

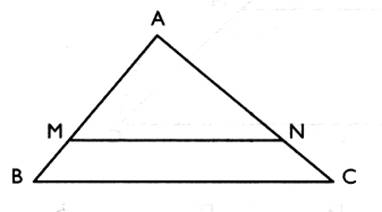
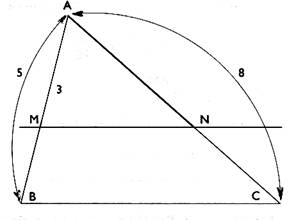
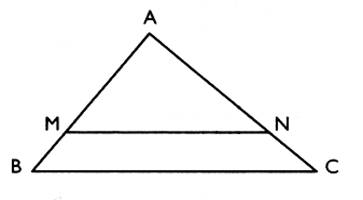
Si dans un triangle A BC , une parallèle à un segment

[ BC] coupe un segment [ AB] en M et un segment

[ AC ] en un point N alors on a

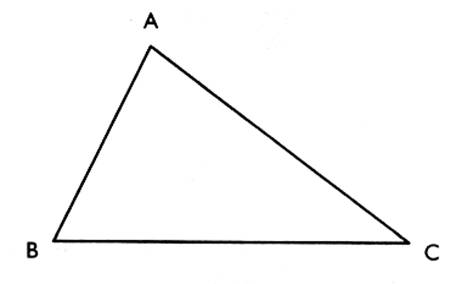
F Activité :

a) Soit un triangle rectangle ABC , quelconque . avec AB = 3 cm , AC = 4,5 cm ,

Placer le point M à 2 cm de A .Construire la parallèle à [ BC ] passant par M ; elle coupe le segment [ AC] en N .

b) Mesurer la longueur du segment AN ( mesure est en cm .) : AN = ……cm

c) Vérifier que :

premier rapport :

deuxième rapport :

Ces deux rapports sont égaux parce que :…………………………

Vérifier que le résultat est égale aux rapports

En conclusion : les droites sécantes forment deux triangles : ANM et ACB

D'après la propriété de Thalès :

On peut écrire : ce qui peut s'écrire , par transformation :

Si dans un triangle A BC , une parallèle à un segment

[ BC] coupe un segment [ AB] en M et un segment

[ AC ] en un point N alors on a

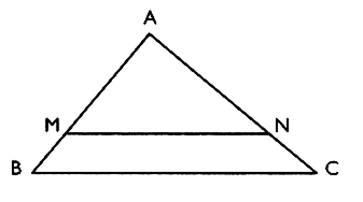
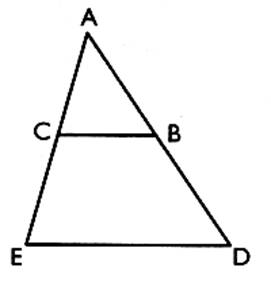
III ) Utilisation de la propriété de Thalès .

Cd :Info plus

F Activité 1 : Dans un triangle ABC , la droite ( MN ) est parallèle à la droite ( BC ).

On a : AB = 5 cm ; AC = 8 cm et AM= 3 cm .

Il est demandé de calculer la longueur du segment AN .

Solution :

La propriété de Thalès nous permet d'écrire :

Les données sont : AN = ……..; AM = ………;NC = ……..; MB = ……..; AC = ……..; AB = ……….

(AN = ? ; AM = 3 ;NC = ? ; MB = 2 = ( 5 - 3 ) ; AC = 8 ; AB = 5 )

On remplace :

On retient que :

Calcul : ( voir le produit en croix ) ; AN = 24 : 5 ; AN = 4,8

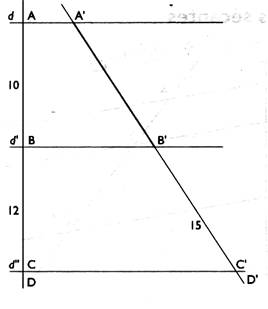
F Activité N° 2 :

On donne trois parallèles coupent deux droites sécantes . On a AB = 10 cm , BC = 12 cm et B'C' = 15 cm . On demande de trouver par le calcul A' B' .

Solution :

D'après la propriété de Thalès , on peut écrire :

Les données sont :

AB = 10 ; A'B' = ? ; BC = 12 ; B' C' = 15 ; AC = 22 ; ( 10 +12) ; A'D' = (A'B' + 15) ;

On remplace :

On cherche A'B' , on retient deux rapports dont on connaît 3 valeurs sur 4 .

; ;

A' B' = 150 : 12 ;

donc A' B' = 12,5

IV ) Généralisations :

CD INFO ++

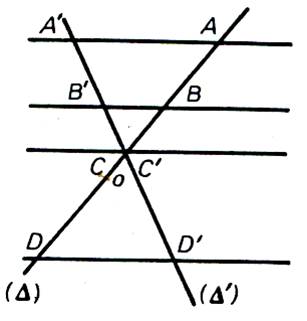
Appliquons le théorème de Thalès 3 droites parallèles ( d) , (d ’) et ( d ’’) coupées par deux droites sécantes ( D) et (D’)

De même pour ( d) , (d ’) et ( d ’’) coupées par deux droites sécantes ( D) et (D’)

cela implique que :

Mais on a aussi : =

On retiendra que :

Des parallèles découpent sur 2 sécantes des segments correspondants proportionnels .

Leçon

TRAVAUX d ’ AUTO - FORMATION sur

N°21

LA PROPRIETE de THALES.

TRAVAUX N°21 d ’ AUTO - FORMATION : CONTROLE

1°) Enoncer la propriété de Thalès relatif à deux droites sécantes coupées par 3 parallèles. ( vous aider d'un dessin)

2°) Enoncer la propriété de Thalès pour un triangle .

En utilisant les caractéristiques de la figure ci - contre .

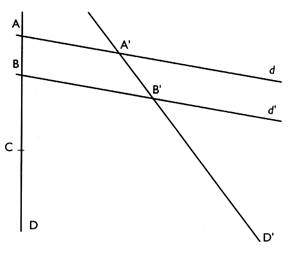
TRAVAUX N° 21 d ‘ AUTO - FORMATION EVALUATION

Exercices traités dans le cours :

1°) Sur la figure , on a tracé D et D' quelconques coupées par deux droites parallèles "d" et "d' " .

"d" coupe D en A et D' en A' . et "d' " coupe D' en B et B' .

Tracer une parallèle à d et d' passant par C et coupant D' en C' .

Relever les mesures et vérifier que

2°) Soit la figure ci - dessous .

On donne : le segment BC parallèle au segment DE , le segment AB = 17 cm , le segment AC = 12 cm et CE = 8 cm. Calculer la longueur du segment AD .

3°) On donne la figure ci-dessous :

AB = 20 cm , BC = 28 cm et A’B’ = 22 cm . Calculer B’C’ .

Exercices non traités dans le cours :

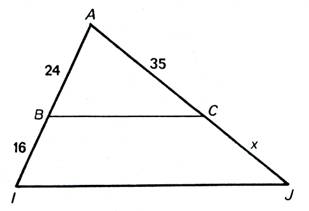
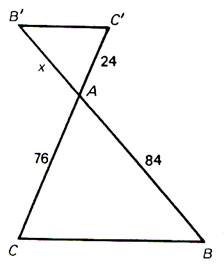
N°1 : Calculer « x »

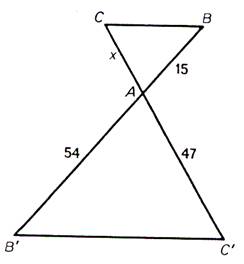
N°2 :

Calculer « x »

N°3 :

Calculer « x » :

N°4 :

Calculer « x » :

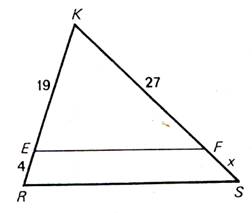
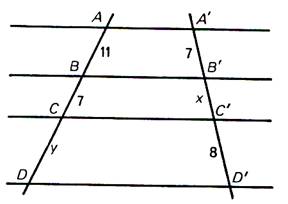
N°5 : Calculer « x » et « y »

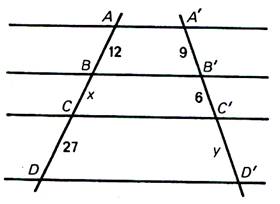
N°6 : Calculer « x » et « y »