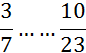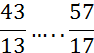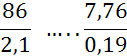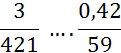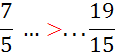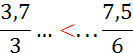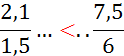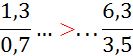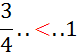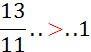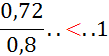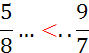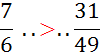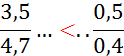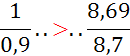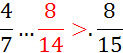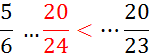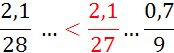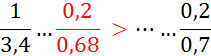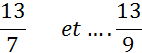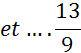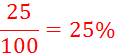Définition de l ‘ objectif : Savoir construire une fraction égale à une fraction donnée.

Pré requis:

	P5 collège	CORRIGE
		Retour Vers les fiches de travail.
Info : Sommaire			Vers le programme de la classe de 5^ème.
Sciences : fractions égales (longueurs)
Fraction nomenclature

ENVIRONNEMENT du dossier :

Retour vers l’accueil « warmaths »

Objectif précédent 1°) fraction égale ( primaire) notions : Travaux : dossier 120 : partage en part égales 2°) Comparaison des fractions à l’unité 3°) Voir cours niveau 6 collège , classe 6^ème collège.

Objectif suivant : 1°) Fractions égales 4^ème s 2°) >> La proportionnalité 3°) Fractions équivalentes 4°) Cours sur les fractions équivalentes et non équivalentes.

Tableau 96 1°) Sommaire : tout sur les transformations d’une fraction. 2°) Sommaire : tout sur la proportionnalité.

Comparaison des nombres en écriture fractionnaire.

Fiche 1 : Comparaison des valeurs décimales exactes ou approchées

Fiche 2 : Les nombres sont représentés par des points d’une droite graduée.

Fiche 3 : Ecritures fractionnaires de même dénominateur.

Fiche 4 : Comparaison à « 1 » ( dit aussi : unité) d’un nombre en écriture fractionnaire.

Fiche 5 : Ecritures fractionnaires de même numérateur

Fiche 6 : Exercices sommatifs.

Fiche 7 : Organisation et gestion de données.

TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité	Corrigé Contrôle	Corrigé évaluation
				Travaux niveau VI et V Dos. 149 comparaison de deux grandeurs.
			Travaux niveau VI et V Dos 160	Travaux : la proportionnalité (fiche 180)

COURS

Fiche 1 : Comparaison des valeurs décimales exactes ou approchées
Comparer deux nombres, c’est dire si ces nombres sont égaux ou dire quel est le plus petit ( ou le plus grand ) des deux.
Exemple 1  : comparons et . Vous savez que et Puisque alors .
Exemple 2  : Comparons les fractions et
Pour cela , nous allons calculer la division : et
	1	1					7			La division ne se termine pas …….
		4	0				1,	5	7
			5		0
					1
		5				3				La division ne se termine pas …….
		2	0			1,	6	6
			2		0
					2
Mais on peut écrire : 1,57 < < 1,58 et 1,66 < < 1,67 Puisque : 1,548 < 1,66 alors ; <
Activité n°…. : Comparez comme précédemment ( en posant les divisons) et
Activité n°…. :
0,428 …< .0,434				3,307 …< ….3,352							40,952 …>….40,842	0,00712…>…0,00711

Fiche 2 : Les nombres sont représentés par des points d’une droite graduée.
ci-dessous on donne une demi-droite régulièrement graduée. L’unité est représentée par « 30 mm » donc « 0,1 » est représenté par «  3 » mm 1 correspond 3 mm ; 0,5 correspond 15 mm , 0, correspond 3 mm.
Donnez l’abscisse des points suivants.
		A ( …. ; ….)		B ( …. ;….)		C ( …. ; ….. )
Les points « A » ; « B » ; « C » , sont placés dans cet ordre , de la gauche vers la droite en partant de la gauche . Leurs abscisses respectives sont rangés dans l’ordre ………..croissant…. En d’autres termes , plus un point est à droite , plus son abscisse est ………..«  élevée , grande… »…
Activité n°…. Sur la demi-droite graduée ci-dessous , placez les points ayant pour abscisse les nombres .
Ce que vous venez de faire vous permet de ranger ces nombres dans l’ordre croissant.

Fiche 3 : Ecritures fractionnaires de même dénominateur.
Sur la droite graduée ci-dessous , on a placé un point d’abscisse «  ». Puisque l’unité est représenté par « 3 cm » , alors «  » est représenté par « 1 cm ». Place de même les points ayant pour abscisse :
Ecrivez les nombres sous la droite comme pour «  »
· Vous pouvez alors ranger les six nombres dans l’ordre croissant : …………………………………………………………………
· Tous ces nombres sont représentés par des fractions qui ont le même …. « dénominateur »…et vous constatez alors que les numérateurs sont rangés dans l’ordre … « croissant » …
Activité n°… : Placez de même sur la droite graduée les nombres :
	3^ème		1^er	5^ème			2^ème		4^ème
Rangez ces nombres dans l’ordre croissant. Vous faites la même constatation que précédemment. Il en serait de même avec n’importe quelles écritures fractionnaires . On dira alors :
A retenir : DE deux nombres représentés par des écritures fractionnaires ( fractions) de même dénominateur, le plus grand est celui dont l’écriture fractionnaire ( fraction) à le plus grand « numérateur ».
Activité ..
Nous allons comparer et . Vous savez que ; on est donc ramené à comparer et . Puisque 13 < 14 , alors < . , c'est-à-dire : < .
Activité n°…. En faisant mentalement comme ci-dessus, complétez en utilisant les signes : < ou >

Fiche 4 : Comparaison à « 1 » ( dit aussi : unité) d’un nombre en écriture fractionnaire.
Comparons «  » à « 1 » . Vous savez que « 1 » peut s’écrire : . et comme «   » ( lire : 7 neuvième est inférieur à neuf neuvième) «  alors  » et vous remarquez que le numérateur de est inférieur à son dénominateur. Activité n°.. En raisonnant comme précédemment, complétez :
Cas général : considérez un nombre dont une écriture fractionnaire est . Comparons –le à la valeur « 1 ».
	Dire que		C'est-à-dire que		C'est-à-dire que «  a . <…b
	Dire que		C'est-à-dire que		C'est-à-dire que «  a . =…b
	Dire que		C'est-à-dire que		C'est-à-dire que «  a . >…b
A retenir : · Toute l’écriture fractionnaire d’un nombre inférieur à « 1 » a son numérateur inférieur à son dénominateur . · Toute l’écriture fractionnaire d’un nombre égal r à « 1 » a son numérateur égal à son dénominateur . · Toute l’écriture fractionnaire d’un nombre supérieur à « 1 » a son numérateur supérieur à son dénominateur .
Activité n°… Comparez : et est très facile , en effet : puisque et alors on peut conclure que
Activité n°… En faisant mentalement comme ci-dessus , complétez en utilisant les signes : < ou >

Fiche 5 : Ecritures fractionnaires de même numérateur.
On vous donne ci-dessous une demi-droite régulièrement graduée sur laquelle il n’y a que « 0 » et « 1 » . L’unité est représentée par « 12 cm ». 1 cm représente donc : et 5 mm représente
· Placez sur cette droite les points d’abscisses.
· Rangez ces nombres dans l’ordre croissant. · Tous ces nombres sont représentés par des fractions qui ont le même numérateur.. et vous constatez que les dénominateurs sont rangés dans l’ordre décroissant..
Remarque : Cela ne doit pas vous étonner : vous savez que quand on partage une grandeur quelconque, plus le nombre de parts est grand plus les parts sont petites .
Activité n°.. : reprenons la graduation de la fiche 3 :
Placez dessus les points d’abscisses :
1,16	0,23		1,4	2,33		0,46	3,5		0,7
« 1 » = 30 graduations ; 0,1 = 1 graduation ;…
Rangez ces nombres dans l’ordre croissant : ;;; ;; ; ; Vous faites la même constatation que précédemment. Il en serait de même avec n’importe quelles écritures fractionnaires. On dira alors :
A retenir : De deux nombres représentés par des écritures fractionnaires de même numérateur, le plus grand est celui dont l’écriture fractionnaire a le plus petit dénominateur.
Activité n°… : Comparons . Vous savez que , on est donc ramené à comparer Puisque 7 < 8 alors c'est-à-dire que .
Activité n°… : En faisant mentalement comme ci-dessus , complétez en utilisant les signes : < ou >

Fiche 6 : Exercices sommatifs.

Exercice 1 : Rangez dans l’ordre croissant les nombres suivants : (vous pouvez les réduire au même dénominateur ) .

Exercice 2 : Rangez dans l’ordre croissant les nombres suivants :

Conseil : commencez par séparer les nombres inférieurs à « 1 » des nombres supérieurs à « 1 » :

Nombres inférieurs à « 1 » :

Nombres supérieurs à « 1 »

En faisant comme l’exercice 1 , complétez : ………..<………<………..<……..<……..< …….

Exercice 3 : Rangez dans l’ordre croissant les nombres suivants :

Commencez par comparer :

Vous pouvez écrire :

Puis comparez

Vous pouvez écrire

:

En définitive :

Fiche 7 : Organisation et gestion de données.
Dans une société comportant « 1300 » salariés , on a voulu se rendre compte de la répartition des âges des salariés . Pour cela, on a constitué « 6 » tranches d’âge et on a compté combien il y avait de personnes dans chaque tranche. Ensuite, on a calculé la fraction du nombre total de salariés correspondant à chaque tranche. On a obtenu le tableau ci-dessous . ( la lettre « A » désigne l’âge.)
Tranche d’âge	A < 20	20 A < 30	30 A < 40	40 A < 50	50 A < 60	60 A
Nombre de salariés	104	195	325	390	260	26
Fraction
Pourcentage	8 %	= 15%		30%	20 %	2%
Angle.	28,8°	54°	90°	108°	72°	7,2
1°) La ligne du tableau donnant le nombre de salariés par tranche a été effacée, on vous demande de la compléter .
Exemple de calcul  : pour la tranche des moins de 20 ans , la fraction du nombre total est de ; le nombre de moins de vingt ans est donc :
2°) Calculez le pourcentage correspondant à chaque tranche d’âge.
Exemple de calcul : pour la tranche des moins de vingt ans on pose : ; le pourcentage est donc d : 8 pour cent que ‘l’on écrit : 8%
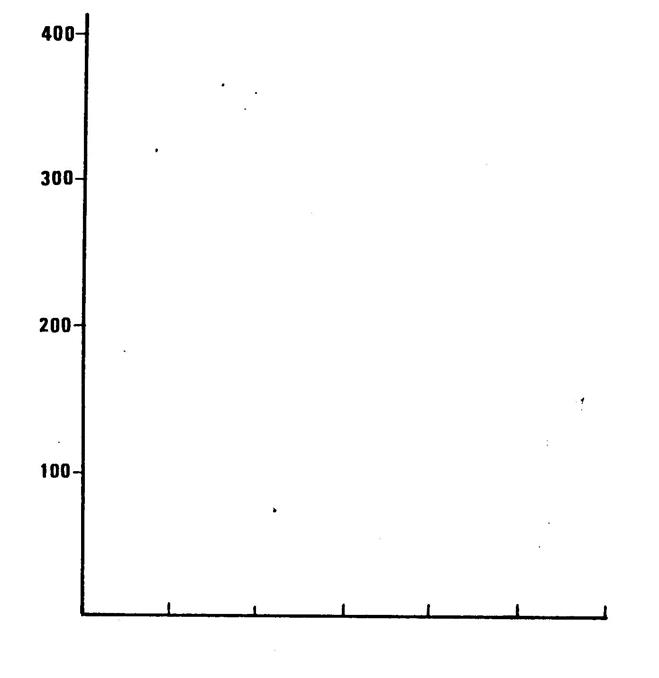
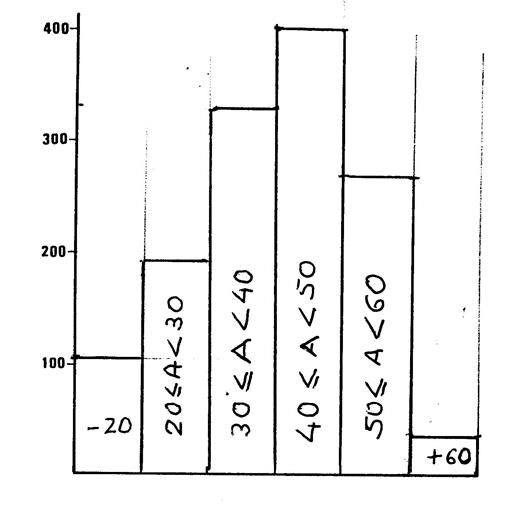
3°) Faite l’histogramme représentant le nombre de salariés correspondant à chaque tranche d’âge . ( voir ci-dessous les axes de coordonnées .)n
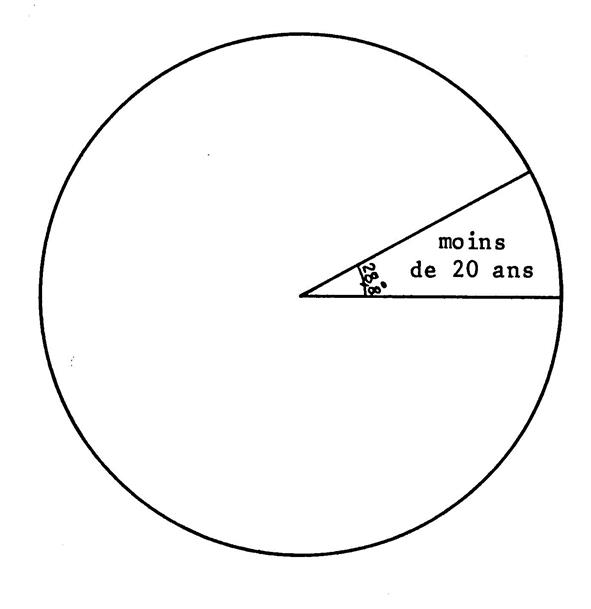
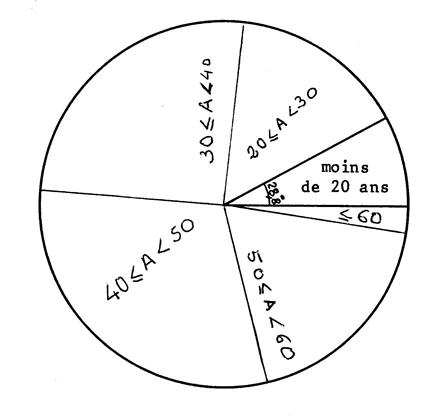
Faites un diagramme circulaire .
Utilisez le disque dessiné ci-dessous.
Vous partagez ce disque en 6 secteurs . Les angles de ces secteurs sont proportionnels aux nombres de salariés . (ou au pourcentage).
A savoir que le disque entier représente les 1300 salariés , il correspond à 360°. Commencez par calculer l’angle de chacun de ces secteurs ( complétez le tableau). Exemple de calcul : le pourcentage des moins de vingt ans est de 8% ; l’angle du secteur le représentant est dons de :

Travaux auto formatifs

CONTROLE:

2 ° ) Par quel signe sont séparées deux fractions équivalentes?

3° ) Que représente deux fractions équivalentes , autre qu ‘une égalité ?

4 ° ) Donnez le modèle mathématique représentant deux fractions équivalentes.

5° ) Comment peut-on procéder pour ordonner ( classer dans un ordre croissant ou décroissant ) des fractions ?

6° ) Comment procède -t - on pour vérifier si deux fractions sont équivalentes (donnez la procédure la plus sûre ) ?

EVALUATION:

I )Dire si les fractions suivantes sont équivalentes (si non les classer par ordre croissant):

a )  ;  ;  ;  ; ; utiliser le tableau ci dessous ;

b )idem que ci dessus :  ; ; ; ;

c ) idem que ci dessus : ; ;

II ) Construire .....5......fractions équivalentes à la fraction donnée :

III) On nous donne deux fractions ; et ;sont-elles équivalentes?

En complément :voir cas avec nombres relatifs

I ° ) Construire 3 fractions équivalentes à la fraction donnée.(indiquer le coefficient multiplicateur utilisé pour chaque étape)

*un « coefficient » est un nombre ,généralement , entier .

a) =

b) =

c) =

d) =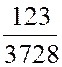

II ° ) CALCUL ALGEBRIQUE :

Mettre sous forme d’une égalité simple les fractions équivalentes suivantes ,en utilisant le produit en croix :

=

=

=

=

et encore :

a) = 5 b) = 7 ;

Construire 4 fractions équivalentes à la fraction à la donnée

a) =

b) =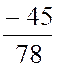

c) =

d) =

Dans les exercices suivants ne pas « développer »

e) =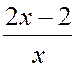

f) =

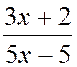CORRIGE EVALUATION

I ) a) ligne 2 : calcul avec la calculatrice

ligne 3 : classement par ordre croissant.

0,28333	0,250	0,8337	0,583	0,600
2	1	5	3	4

conclusion : < < 7/ 12 < <

Interdisciplinarité

Voir «  les proportions »