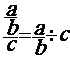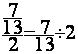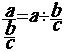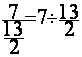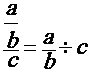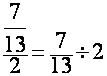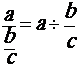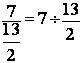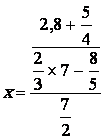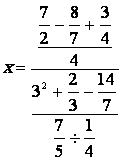|
|
Devoir : Ÿ Remédiation : Ÿ |
Nom :………… |
Classe : Groupe :
|
|
|
Date :…………… |
Rattrapage : Ÿ Soutien : Ÿ |
Prénom :………… |
Note contrôle : |
Note évaluation : |
|
|
Définitions préalables
1°) donner
la définition d’un fraction : donner un exemple avec 3 et 4
Exemples : 
ou 
2°) Qu’est
ce qu’un rationnel ?
Donner des exemples :
16 : 2 = ?
25: 4 =
?
11 : 7 =
?
3°) qu’appelle - t - on
« écriture fractionnaire »
|
A. ADDITION ; SOUSTRACTION ;
MULTIPLICATION ; DIVISION de DEUX
FRACTIONS DE MEME DENOMINATEUR . |
|
1. ADDITION |
1°) A quoi est égale la somme de deux
fractions ? (
Forme littérale)
2°) Donner la Forme symbolique mathématique:
Calculer :
|
2.SOUSTRACTION |
1°) A quoi est égale la différence de deux
fractions de même dénominateur ? ( Forme littérale)
L
2°) donner
la Forme symbolique mathématique:
calculer :
Calcul
de : 
; donner le résultat sous forme irréductible et sous forme décimale à 0,01
prés .
|
3.MULTIPLICATION |
1°) A quoi est égale la différence de deux
fractions de même dénominateur ? ( Forme littérale)
2°) donner sa forme symbolique mathématique:
Calculer 
donner le
résultat sous forme irréductible et sous
forme décimale à 0,001 prés .
|
4
.DIVISION |
1°) Compléter la phrase :
Remarque importante:
Nous calculer directement la
fraction de deux fractions ,il faut impérativement
transformer
2°) Transformer la fraction de fractions en
division de fractions :
3°)
transformer 
en une division de deux fractions :
4°)
A quoi est égale le résultat de la division de deux fractions de même dénominateur ? ( Forme
littérale)
5° ) montrer les étapes de transformation conduisant au
résultat .
Calculer :
EVALUATION :
|
Addition |
|
|
|
|
|
|
|
Soustraction
( pour cet exercice il faut avoir fait la
leçon sur les nombres relatifs) |
|
|
|
|
|
|
|
Soustraction |
|
|
|
|
|
|
|
Multiplication |
|
|
|
|
|
|
|
Fraction de fractions |
|
|
|
|
|
|
|
Division de fractions |
|
|
|
|
|
|
=
Réponses : 
; 
; 
; 
; 
; 
|
B )
ADDITION ; SOUSTRACTION ; MULTIPLICATION ; DIVISION
de DEUX FRACTIONS DE DENOMINATEURS DIFFERENTS. |
|
5
.ADDITION : |
1°) Soit les deux fractions 
que peut - on déclarer sur l’addition de ces deux
fractions ?:
2°)Ainsi avant de faire l’addition de deux
fractions de dénominateurs différents il
faut transformer chaque fraction en fraction dites « …………………………» dont le nouveau dénominateur est « bd » ( ……………………………………..)
.
3°) transformer 
en fraction équivalente de dénominateur valant
« bd »
4°) transformer 
en fraction
équivalente de dénominateur valant « bd »
5 ° )
faire l’addition des fractions : 
Calculer : 
|
6. SOUSTRACTION: |
1°) Soit les deux fractions que peut - on déclarer sur la soustraction de ces deux fractions ?: .
2°)Ainsi avant de faire l’addition de deux
fractions de dénominateurs différents il
faut transformer chaque fraction en fraction dites « …………………………….. » dont le nouveau dénominateur est « bd » ( …………………………………………..)
.
3°) transformer en fraction équivalente de dénominateur valant
« bd »
4°) transformer en
fraction équivalente de dénominateur valant « bd »
5 ° )
faire la soustraction des fractions :
Calculer 
|
7.MULTIPLICATION |
1°) à quoi est égale la multiplication de deux
fractions de dénominateurs
différents ? ( écriture littérale) ?
2°) donner la traduction symbolique
mathématique: 
= 
= 
3°) Calculer : 
; donner le résultat sous forme
irréductible et puis sous forme décimale à 0,001 prés .
S
|
8. DIVISION |
1°) Compléter la phrase :
Remarque
importante: Comme pour la division de deux fractions de même
dénominateur , nous ……………………………………………………. calculer
directement la fraction de deux fractions de dénominateur différent , il faut impérativement transformer
2°) Transformer la fraction de fractions en
division de fractions :
3°) transformer
en une division de
deux fractions :
L
4°)
A quoi est égale le résultat de la division de deux fractions de même dénominateur ? ( Forme
littérale)
5° ) montrer les étapes de transformation conduisant au
résultat .
3°) Donner la forme symbolique mathématique
du calcul de 
?
Calculer 
? ;
donner le résultat sous forme irréductible et puis sous forme décimale à
0,001 prés .
EVALUATION
|
Addition |
|
|
|
|
|
|
|
Soustraction
( pour cet exercice il faut avoir fait la
leçon sur les nombres relatifs |
|
|
|
|
|
|
|
Soustraction |
|
|
|
|
|
|
|
Multiplication |
|
|
|
|
|
|
|
Fraction de fractions |
|
|
|
|
|
|
|
Division de fractions |
|
|
|
|
|
|
=
|
C)
ADDITION ; SOUSTRACTION ; MULTIPLICATION ; DIVISION d’ UNE FRACTION et d’UN NOMBRE . |
|
9. ADDITION |
1° )
On ne peut pas additionner ( 
= ?….) une fraction avec un nombre
entier (naturel ou relatif) que faut-il faire pour obtenir un résultat ?
2° )
Modèle mathématique: = ?
3°) Calculer : 
= ? ou 
Procédure pour transformer l ‘ addition
( ou la soustraction ) en addition ( ou soustraction) de deux
fractions de même dénominateur.
1°)Rendre la
fraction
irréductible.:
cette fraction est irréductible
Exemple : 7 /13
= 
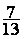
2°)Mettre le nombre
sous forme de fraction de dénominateur égal à
1
Modèle mathématique: c = 
;
Exemple : 2
= 
3°)Transformer cette fraction en fraction
équivalente de dénominateur égal au dénominateur de la première
fraction.
Modèle mathématique: 
Le dénominateur de la première fraction est
13
donc 
=
4°) Poser la nouvelle égalité
Modèle mathématique: = 
donc
= 
5°) Faire l’addition des deux fractions de même dénominateur. 
donc
= 
6° ) il faudra conclure (comme on l’a vu
pour les exercices précédents ), après
vérification.
|
10.SOUSTRACTION |
Soustraction d’une fraction avec un nombre
entier (naturel ou relatif)
Modèle mathématique: 
= ?
pas de solution
immédiate; (il faut transformer)
Exemple: 
= ?
on ne peut obtenir le résultat
directement,
Il faut
transformer la soustraction donnée en
soustraction de deux fractions de même dénominateur
iContrairement à l’addition , pour la soustraction , si l’on permute le
nombre et la fraction on n’aura pas le
même résultat: 
¹ 
Procédure pour transformer la
soustraction d’un nombre et d’une
fraction en soustraction de deux fractions de même dénominateur.
(
nous ne traiterons que
l’exemple de soustraction : )
procédure :
1°)Rendre
la fraction
irréductible.:
Exemple : la fraction irréductible de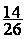 
est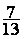
2°)Mettre le nombre
sous forme de fraction de dénominateur égal à 1
Modèle mathématique: c = ; exemple : 2
=
3°)Transformer cette fraction en fraction
équivalente de dénominateur égal au
dénominateur de la première fraction.
Modèle mathématique:
Le dénominateur de la première fraction est
13
donc
4°) poser la nouvelle égalité
Modèle mathématique: 
= 
donc
= 
5°) faire la soustraction des deux fractions de même
dénominateur.
donc
= 
6° ) il faudra conclure (comme on l’a vu
pour les exercices précédents ), après
vérification.
|
11 .MULTIPLICATION |
|
Par
définition : On ne peut pas multiplier un nombre par une fraction , pour obtenir un résultat on prendra appui sur
la règle concernant la multiplication de deux fractions . |
Modèle mathématique: 
=
Exemple
: 
= ? ;
pas de solution immédiate . Il faut transformer
la multiplication d’une fraction par un nombre (entier naturel ou relatif) par
une multiplication de deux fractions:
On passe de ce modèle mathématique: 
à ce modèle 
Mettre le nombre « c » sous forme de
fraction de dénominateur égal à 1 ;
tel que c =
3° )
On applique la procédure concernant la multiplication de deux fractions:
=
4° )
Rendre compte: 
=
Exemple : 
=
Solution : = 
= 
= 
Forme irréductible
Conclusion : = Forme décimale arrondie à
0,001 prés : 1,077
Cas particulier 1 : on veut calculer : 3
= ; 
72
Modèle mathématique: 
a = pas
de solution immédiate ; (il faut
transformer)
|
|
Exemple :
si b = 2
Exemple
1 :
( donner le résultat sous forme d’une fraction simplifiée ; puis
sous la forme décimale )
remarque : (
= 0,5 ),
sous forme décimale 3 = 0,5
Calculer 3 =
3 = 
( voir multiplication de deux fractions)
= 
; =
(voir
simplification d’une fraction)
= 
; = 
; =
conclusion : 3 =
Exemple
2 : calculer
72 ( donner le
résultat sous forme d’une fraction
simplifiée ; puis sous la forme décimale )
72 = 
=
; 
= 
; 
Conclusion : 72 = ou 72 = 18
|
12. DIVISION |
Attention:
on ne doit pas confondre:
« diviser une fraction par un nombre(
entier) » ( 1° cas):
|
|
|
« diviser un nombre ( entier) par une
fraction »(2° cas)
|
|
|
iCe
qui différencie les deux cas est la position du signe « égal »
devant l ‘ une des deux barres de
fraction :
Etude
du 1° cas : « diviser une fraction par un nombre(
entier) »
|
|
|
1°) Première transformation
Exemple: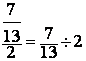 
On
transforme l’écriture la fraction par un
nombre par la division d’une fraction par un nombre .
2°) Deuxième transformation
Transformer
« le nombre "2" » en
fraction de numérateur égal à 1.
2 = 
3°) Troisième transformation : seconde. »
= « On multiplie la première fraction par l
‘inverse de la seconde fraction ! »
4°) Calcul : appliquer la règle concernant la
multiplication de deux fractions.
= 
» 0,269
( résultat sous forme décimale à 0,001 près )
Etude du
second cas :
Division d’un nombre "a"
entier par une fraction
|
|
|
Pour
obtenir un résultat ,on opèrera par
transformations successives
Exemple :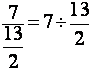 
Première
transformation :On transforme la « double » fraction par la
division d’un nombre par une fraction .
1°) Transformer la division d’un nombre par
une fraction en une division de fraction
par une fraction.
Deuxième
transformation : mettre le
nombre « 7 » en fraction de dénominateur égal à 1.
7 = 
2°) Multiplier la première fraction par l
‘inverse de la seconde. »
Troisième
transformation : dans la fraction de fractions , il faut multiplier la première
fraction par l’inverse de la seconde fraction.
4°) Faire la
multiplication des deux fractions.
ion peut constater que les deux cas donnent des résultats différents
,il est donc trés important de vérifier la position
du signe « égal »
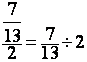donne comme résultat: 
» 0,……
et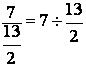 
donne comme
résultat: 
»
1,……
+Faire
les exercices suivants
|
Addition |
|
|
|
|
|
|
|
Soustraction
( pour cet exercice il faut avoir fait la
leçon sur les nombres relatifs) |
|
|
|
|
|
|
|
Soustraction |
|
|
|
|
|
|
|
Multiplication |
|
|
|
|
|
|
|
Fraction de fractions |
|
|
|
|
|
|
|
|
|
|
|
Division de fractions |
|
|
|
|
|
|
|
|
|
|
( Voir la partie abordée dans la leçon N°2 sur
la fraction)
A savoir :
a% = 
« a » pour « cent » est une donnée statistique
Pour
savoir plus d’informations sur cette équation
il faut voir la leçon sur la fonction linéaire
y = x ; ou
y = 
= 
= 
ou « y »
est la valeur d’une augmentation ou diminution
« a »
la valeur du taux
« x »
le nombre sur lequel s’applique le taux.
Exemple :
on veut calculer 8 % de 120
On transforme : 8% = 
( = 0,08 )
On calcule : ´
120 = 
= 
= 
= 9,6
Conclusion :
8% de 120 = 9,6
|
Leçon |
Titre |
|
N°5 |
TRAVAUX d ’ AUTO - FORMATION
sur
LES NOMBRES |
1°) Citer la règle concernant l ‘ addition de deux
fractions de même dénominateur .
2°) Citer la règle concernant la soustraction de
deux fractions de même dénominateur .
3°) Citer la règle concernant la multiplication de deux fractions de même dénominateur .
4°) Citer la règle concernant la division de deux
fractions de même dénominateur. .
5°) Que faut-il faire avant d’additionner ou soustraire
deux fractions de dénominateur différent ?.
Série 1 :
|
Calculer |
Passage intermédiaire |
Résultat |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=
|
CORRIGE de la série B ci dessous . ( C d : cliquer
sur le bille )
|
Série B :d’ exercices sur les « fractions » :
|
I) rendre irréductibles
les fractions suivantes : |
Résultats
|
|
|
|
ADDITIONNER
|
N°1 |
Résultats |
|
|
|
|
N° 2 |
résultats |
|
|
|
SOUSTRAIRE :
|
N°1 |
|
|
|
|
|
N°2 |
|
|
|
|
EFFECTUER :
|
|
|
MULTIPLIER :
|
N°1 |
|
|
|
|
|
N°2 |
|
|
|
|
DIVISER :
|
N° 1 |
|
|
|
|
|
N° 2 |
|
|
|
|
EFFECTUER :
Calculer et
exprimer le résultat sous les trois formes suivantes:
Sous forme d'une fraction
Sous forme d'une fraction irréductible
Sous forme décimale , donnée par votre calculatrice ;
à 0,001 prés
|
N°1 |
|
|
|
|
|
N°2 |
|
|
|
|
|
N°3 |
|
|
|
|
|
N°4 |
|
|
|
|
|
N°5 |
|
|
|
|
|
N°6 |
|
|
|
|
|
N°7 |
|
|
|
|
|
N°8 |
|
|
|
|
|
N°9 |
|
|
|
|
|
N°10 |
|
|
|
|
|
N°11 |
|
|
|
|
PROBLEMES :FRACTIONS ( Série1)
FRACTION
D'UNE GRANDEUR
1)
Une salle de cinéma qui compte 320 places est
remplie aux ¾. Combien y a-t-il de places occupées ? Combien reste-t-il de
places libres ?
2)
La France a une superficie de 549 000 km² dont ¼ est
recouvert de forêts. Quelle est la superficie de la forêt française ?
3)
Une famille répartit ses revenus en prévoyant
notamment : 2/20 pour les impôts, 5/20 pour l'alimentation et 3/20 pour le
loyer. Les revenus mensuels de la famille étant de 15 500 F, calculer en
francs, le montant des dépenses prévues pour les impôts, l'alimentation et le
loyer.
4)
Les 4/10 des 330 000 habitants de la
Martinique ont moins de 20 ans. Trouver la question et y répondre.
5)
Une personne qui a gagné 107 800 F au Loto offre 1/7
de son gain à l'association "Médecins du Monde" et 3/7 à une
association pour la recherche contre le cancer. Quelle somme a-t-elle offerte à
chacune de ces associations ? Combien a-t-elle gardé ?
6)
Sur un terrain constructible de 1 395 m², 1/9 est réservé à la maison et 2/5
au jardin potager. Le reste de la surface sera ensemencé en pelouse. Quelle sera
la superficie occupée par cette pelouse ?
7)
Le vélo de cross d'Alain vaut 720 F. Celui de
Stéphane coûte les 9/6 de celui d'Alain. Quel est le
prix du vélo de Stéphane ?
8)
Maman a 33 ans. L'âge de Papa est égal aux 7/6 de celui de Maman. Quel est l'âge de Papa ?
9)
Des maçons doivent construire un mur de 25 m de
long. La première journée, ils en édifient les 2/5, puis ¼ le lendemain. Quelle
longueur de mur leur restera-t-il à construire le troisième jour ?
10)
Romain prépare un cocktail pour ses camarades. Dans
un saladier d'une capacité de 3,5 l, il doit verser 3/10 de jus d'ananas, 1/5
de jus d'orange, 1/14 de sirop de grenadine et compléter avec de l'eau gazeuse.
Quelle quantité (en litres) de chaque ingrédient doit-il utiliser ?
11)
Pour arroser son jardin, papa récupère l'eau de
pluie dans une citerne, d'une capacité de
2 700 l. Celle-ci est actuellement rempli aux
4/5. Sachant qu'il utilise environ 90 l d'eau par jour, en aura-t-il
suffisamment pour une durée de trois semaines sans pluie ?
12)
Un jardinier dispose d'une citerne d'une capacité de
2 500 l. Il en tire d'abord 1/5, puis les 3/5 de ce
qu'il reste. Quelle quantité d'eau, en litres, a-t-il utilisée chaque fois ?
Quelle quantité d'eau reste-t-il dans la citerne ?
13)
Monsieur Léman achète un canapé valant 23 750 F. Il
paie 1/8 de cette somme à la commande, 3/8 à la livraison et le reste en 4
mensualités égales. Combien verse-t-il à la commande ? A la livraison ? Combien
versera-t-il à chaque mensualité ?
14)
Un train peut transporter 420 voyageurs, mais il
n'est plein qu'aux 5/7. Un quart des passagers voyage
en première classe. Combien de personnes voyagent en seconde classe ?
15)
Pour un match de football international, les 7/8 des 50 000 places du Parc des Princes sont occupées.
4/5 des spectateurs ont payé leur place, les autres bénéficient d'invitations.
Quel est le nombre de spectateurs assistant gratuitement au match ?
16)
Le grand frère de Mathieu achète une moto valant 8
880 F. Il verse d'abord 1/3 de cette somme à la commande, puis, à la livraison,
les ¾ de ce qu'il devait encore. Ses parents paient le reste. A combien s'élève
la participation de ses parents ?
17)
L'Europe compte environ 800 millions d'habitants,
soit à peu près le 1/6 des hommes vivant sur la Terre, mais elle n'occupe que
le 1/16 des continents qui couvrent 136 millions de km². Quelle est, environ,
la population de la Terre ? Quelle est la superficie de l'Europe ?
1)
Un concurrent à moto du rallye Paris -Dakar tombe et
abandonne aux 6/7 de la compétition après 18 jours de
course. Quelle est, en jours, la durée totale de l'épreuve ?
2)
Patrick revend son skate-board ; avec les 2/3 de ce
qu'il a ainsi gagné, il s'achète un disque valant 65 F. Combien avait-il
revendu son skate-board ?
3)
On achète une voiture d'occasion coûtant les 5/8 du prix du même modèle, à l'état neuf. Si l'on a
payé cette voiture 43 200 F, combien valait-elle neuve ?
4)
Dans un appartement, la salle de bains occupe les
2/35 de la superficie habitable, soit 6,5 m². Calculer la superficie habitable
de cet appartement.
5)
Une bouteille est remplie aux
2/3. Il faudrait y ajouter encore 25 cl pour la remplir complètement. Quelle
est la capacité de cette bouteille ?
6)
A la Bourse, un homme d'affaires perd les 4/7, soit
280 000 F, de son capital. Quel était le capital initial ? Calculer le montant
de la perte si elle avait correspondu aux 3/5 du
capital.
7)
Ingrid partage avec ses 3 frères et sœurs les 5/7 de
son gain au Loto et , avec le reste, achète une plante
verte pour sa mère. Chacun des enfants reçoit 35 F. Combien Ingrid avait-elle
gagné ? Quel est le prix de la plante verte ?
CORRIGES des Activités
« cours »
|
ACTIVITES
1 |
Faire les exercices
suivants :
|
Addition |
|
|
|
|
|
|
|
Soustraction
( pour cet exercice il faut avoir fait la
leçon sur les nombres relatifs |
|
|
|
|
|
|
|
Soustraction |
|
|
|
|
|
|
|
Multiplication |
|
|
|
|
|
|
|
Fraction de fractions |
|
|
|
|
|
|
|
Division de fractions |
|
|
|
|
|
|
Réponses : ; ; ; ; ;