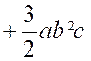Nous avons déjà vu comment on indique, par signes, l'addition, la soustraction, la multiplication division des quantités algébriques, et c'est l'emploi de ces signes qui a donné naissance aux expressions littérales que nous avons appelées monômes et polynômes . Mais ces quantités littérales elles-mêmes, avec leurs signes, leurs lettres, leurs coefficients et leurs exposants sont soumises à leur tour aux quatre opérations fondamentales, d'après des règles qui constituent le calcul algébrique.

Ces opérations rappellent en général mômes idées qu'en arithmétique, et comportent mêmes définitions.

La multiplication algébrique

Nous avons dit ( info retour ) que l'emploi des lettres nous dispensait d'écrire le signe X pour indiquer le produit des divers facteurs qui entrent clans un monôme, c'est-à-dire que 8 a b revient à 8 x a x b. Nous nous rappelons aussi l'emploi des exposants par lequel a ⁵b³d égale aaaaa x bbb x c.

Nous savons, de plus , que le produit de plusieurs facteurs reste le même dans quelque ordre qu'on effectue la multiplication; par exemple, que a x b x c = b x.a x c = b x c x a

Cela posé, occupons-nous de, la multiplication algébrique.

Multiplication des monômes.

Supposons d'abord que les facteurs monômes soient positifs, pour n'avoir pas encore à nous occuper des signes ; la considération des coefficients, des lettres et des exposants nous fournira les trois règles suivantes :

règle des coefficients : Le coefficient du produit se forme en multipliant entre eux les coefficients numériques des facteurs monômes, d'après les règles ordinaires de l'arithmétique.

Ainsi le produit de 6a par 4b sera 24a b ; en effet 6 a X 4 b revient à 6 x a x 4 x b;ou bien, en changeant l'ordre des facteurs. 6 x 4 x a x b = 24a b .

règle des lettres : II faut écrire au produit toutes les lettres qui entrent dans chacun des facteurs monômes, et les placer les unes à la suite des autres dans un ordre quelconque.

Ainsi le produit de a*ô par mn sera a² b par mn sera a ² b m n, ou bien m n a² b.

Cette règle découle des conventions rappelées ci- dessus.

REGLE DES EXPOSANTS :

Quand une même lettre se trouve dans les divers facteurs, on ne l'écrit qu'une fois au produit, mais on lui donne pour exposant la somme des exposants qu'elle avait dans les facteurs réunis .

Soit à multiplier a³ b ² c par a² b c, le produit, sera a⁵ b ³ c² .

En effet, a³ b ² c x a² b c est égal à a a a b b c x a a b c, ou bien, on intervertissant l'ordre des facteurs, à aaaaa x bbb x cc ; or, d'après la signification des exposants, (info ? ) , ce dernier produit revient à celui indiqué ci-dessus a⁵ b ³ c² .

Ces trois règles se résument en une seule règle : Pour multiplier deux monômes, il faut d'abord faire le produit des coefficients numériques, écrire à sa suite,comme facteurs, les lettres communes aux deux monômes donnés, après avoir ajouté leurs exposants, enfin mettre telles quelles les lettres qui sont différentes.

D'après cette règle, on aura :

12a4 b² c x 3a² b m ² = 36 a⁷ b ³ c m ²

Passons maintenant à la règle des signes. Le signe du produit dépend des signes des deux facteurs, et ceux-ci peuvent être tous les deux positifs ou tons les deux négatifs, ou bien l'un positif et l'autre négatif.
Cela posé :

règle des signes. Le produit est positif toutes les fois gué les deux facteurs ont le même signe, il est négatif quand les facteurs sont de signes contraires,

Le tableau suivant exprime cette règle :

+ a x + b = + ab

— a x — b = + ab,
+ a x — b = — ab,

— a x + b = — ab,

et on l'énonce en disant : + multiplié par + ou — multiplié par — donne + ; et + multiplié par — ou — multiplié par + donne —.

Démonstration. La démonstration de cette règle sera divisée en deux parties; dans la première, nous considérerons le cas où le multiplicateur est positif, le multiplicande étant quelconque, et ensuite le cas où le multiplicateur est négatif.

1^er cas		2^ème cas

+ a	- a	+ a	- a
+ b	+ b	- b	- b
+ ab	- a b	- a b	+ ab

1°) Multiplier + a par + b , c’est ajouter à elle-même « a » autant de fois qu'il y a d'unités dans « b » , c'est à dire c'est : a + a + a ..... = + ab

De même, multiplier — a par + b , c'est encore ajouter à elle-même la quantité négative — a autant de fois que l'indique le multiplicateur b ; c'est donc

-a – a – a …….= — ab.

2° En second lieu, le signe — étant le signe de la soustraction, le multiplicateur négatif indique qu'il faut soustraire le multiplicande autant de fois qu'il y a d'unités dans le multiplicateur ; ainsi + a x - b signifie que a doit être retranché b fois, ce qui donne :

- a – a – a …….= - ab

Enfin, - a multiplié par - b reviendra à retrancher - a autant de fois que l'indiqué b , et donnera + a + a + a +……..= + ab

La démonstration est donc complète, et l'on écrira, d'après cette règle :

-18 a³ b x + 7 abm = - 126 a ⁴ b² m

et - 3 ab x – ½ bc = =

Observation. Dans l'application des règles précédentes, les élèves ne doivent pas perdre de vue que tout terme écrit sans signe est positif, et qu'un terme sans coefficient ni exposant exprimés a l'unité pour coefficient et pour exposant (Voir les exercices n°* 40, 4i, 42, 43, 44, 48.)...

Entraînement : faire les exercices ci-dessous

	1°) . Quel est le produit de14a³b²c par 9abdm ?

	2°) Multiplier : - ¾ mn par 36 mx

	3°) Effectuer le produit de 8 ab³ y par — 7 a² cx

	4°) Faire le produit de – 5 a b² x² par – 12 amx

	5°) Trouver le produit des trois facteurs 5 a b ( - 3 b c ) ( + 7 ad)

	6°) Effectuer l’opération :
	( 13 ab ) ( - a²) =

	Multiplication des polynômes
	Pour effectuer la multiplication des polynômes entiers en « x » , il n’y a qu »à appliquer la propriété distributive ( voir info @ cours ).concurremment avec la règle d’addition des exposants.( voir info @ cours) . C’est ce que l’on appelle « développer » . Il ne reste plus qu’à « réduire » et « ordonner »
	Donc , la multiplication des polynômes se réduit à une suite de multiplications de monômes, en observant pour chacun d'eux les règles des signes, des coefficients, des lettres et des exposants. On peut donc énoncer cette opération de la manière suivante : règle. Pour faire le produit d'un polynôme par un autre,- multipliez successivement tous les termes du multiplicande par chacun des termes du multiplicateur, en observant la règle des monômes, et ensuite opérez la réduction des termes semblables que peuvent renfermer les produits partiels Appliquons cette règle aux exemples suivant :

	N°1 : P = ( x ² + 3 x – 4 ) ( x ³ + x + 2 )
	= x ⁵+ x ³ + 2 x² + 3 x ⁴ + 3 x² + 6 x - 4 x ³ - 4 x - 8 = x ⁵+ 3 x ⁴ + x ³- 4 x ³+ 2 x² + 3 x² - 4 x - 8 P = x ⁵+ 3 x ⁴ - 3 x ³+ 5 x² - 4 x - 8
	N°2 :

Multiplicande	5 a³	- 7 a²b	+ 3ab²	+ 4b³
Multiplicateur		3a²	— 8 ab	— b²
			- 5 a³ b²	+ 7 a²b ³	- 3 a b⁴	- 4 b⁵
		- 40 a ⁴ b	+ 56 a ³ b²	- 24 a² b³	- 32 a b⁴
	+ 15 a ⁵	- 21 a ⁴ b	+ 9 a ³ b²	+ 12 a² b ³
Total :	+ 15 a ⁵	- 61 a ⁴ b	60 a ³ b²	- 5 a² b ³	- 35 a b⁴	- 4 b⁵

Pour former ce produit on a d'abord ordonné les deux facteurs par rapport à « a », après quoi l'on a multiplié tous les termes du multiplicande par le premier terme « - b² » du multiplicateur, ce qui a donné

- 5 a³ b²

+ 7 a²b ³

- 3 a b⁴

- 4 b⁵

ensuite on a fait le produit de tous les termes du multiplicande par le 2^ème terme — 8 ab du multiplicateur, et l'on a obtenu :
	- 40 a ⁴ b	+ 56 a ³ b²	- 24 a² b³	- 32 a b⁴
qu'on a écrit au-dessous de la première ligne en faisant correspondre les termes semblables ; de même, le produit du multiplicande le 3^e terme « 3 a² » du multiplicateur a fourni la 3« ligne

+ 15 a ⁵

- 21 a ⁴ b

+ 9 a ³ b²

+ 12 a² b ³

qu'on a posée sous les autres dans l'ordre indiqué; enfin, la réduction opérée sur tous les produits partiels, en ayant soin de bâtonner les termes semblables, a donné le produit demandé.

Démonstration. Cette règle repose sur le principe qui sert de base en arithmétique à la multiplication de deux nombres quelconques (info +++7) ; en effet, de même que la multiplication de 3657 par 543 revient à répéter le multiplicande 3 fois, plus 40 fois, ensuite 500 fois, ce qui donne trois produits partiels, de même en algèbre on fait le produit du multiplicande par chacun des termes du multiplicateur.

Avant d'effectuer la multiplication, il est avantageux d'ordonner les deux polynômes par rapport à la ' môme lettre ; ensuite on place les produits partiels de manière que les termes semblables soient sur une même colonne; par là la réduction est plus facile.

· Remarque I. Quand les deux facteurs sont ordonnés par rapport à la même lettre, le produit se trouve nécessairement ordonné de la même manière ; mais ce qu'il importe de remarquer, c'est que le premier produit monôme 15 a⁵et le dernier - 4b² ne peuvent pas avoir de termes semblables et sont par conséquent le premier et le dernier terme du produit total. En effet, le premier 15 a⁵provient de la multiplication du premier terme du multiplicande par le premier terme du multiplicateur, et alors l'exposant de la lettre principale dans ce produit est plus élevé que dans tous les autres termes ; par une raison analogue, le produit monôme - 4b² , qui résulte des deux derniers termes des facteurs, sera le seul qui ne contienne pas la lettre principale, ou il la contiendra avec le plus faible exposant.

Cette remarque importante sert de base à la théorie de la division !!!.

Remarque II. Lorsque l’on veut indiquer le produit de deux polynômes sans effectuer la multiplication, on enferme chaque facteur entre deux parenthèses, et on les place l'un contre l'autre sans autre signe intermédiaire.

Ainsi, pour indiquer la multiplication de 8a² + 5a² b - 3 a b² par 12a² - 7 b² , on écrira : ( + 5a² b - 3 a b² ) (12a² - 7 b²)

De même, l'expression (a² - b ² ) ( a + b) ( m² + 2 n – n² ) représente le produit des trois facteurs a² - b ² ; a + b ; m² + 2 n – n².

Enfin, 12a² ( m + n ) indique la multiplication du binôme m + n par 12a²

· Au lieu de parenthèses on se sert quelquefois de crochets [ ] , et leur emploi même est indispensable dans le cas de doubles parenthèses ; ainsi, quand on veut indiquer qu'une expression de la forme ( a + b) x - b² doit être multipliée par un autre facteur 3 a² , on écrit 3 a² [ ( a + b) x - b² ]

· Comme on le voit, le concours des crochets et des parenthèses indique deux opérations successives à effectuer

Remarque III . D'après la règle de la multiplication, quand un polynôme a été multiplié par un monôme, ce monôme se trouve facteur dans chacun des termes du produit ; ainsi 2 a² - 3 ab + b² multiplié par m donne 2 a²m - 3 abm + b² m

Réciproquement, lorsque tous les termes d'un polynôme contiennent des facteurs communs, on peut considérer le monôme résultant de ces derniers comme un multiplicateur introduit dans le polynôme et que l'on peut en séparer de nouveau.. C’est ainsi qu’après avoir . reconnu que tous les termes du polynôme ci-dessus 2 a²m - 3 abm + b² m contiennent le facteur m, on l'enlèvera pour l'écrire en dehors des parenthèses qui renfermeront le polynôme restant, comme ci-après :

m (2 a² - 3 ab + b² ).

On trouverait de même que le polynôme « 5 a² x³ + 15 a ³ b² - 10 a⁴x » dont les termes contiennent le facteur commun 5 a² , revient à : « 5 a² ( x³ + 3 a b² - 2 ²) »

Enfin, autre exemple , on a évidemment a²x² - x² = x² ( a² - 1 ) .

Effectuer ces décompositions, c'est ce qu'on nomme en algèbre mettre en facteur commun, opération d'un usage fréquent.

Remarque IV, Une quantité, multipliée plusieurs fois par elle-même, donne un produit qui porte en général le nom As puissance; cette quantité est dite la racine de la puissance ; le nombre de fois que la quantité
entre comme facteur dans ce produit est le degré de la puissance, et nous savons déjà que l'exposant marque ce degré ; ainsi :

a, a*, a³, a⁴, a⁸,., etc

indiquent la 1^ère , 2^e, 3^e, 4^ème ", 5^ème , etc., puissance de « a ». La seconde puissance s'appelle ordinairement le carré, et la troisième le cube.

Quand le degré d'une puissance est indifférent, indéterminé, on le marque par une lettre en exposant; ainsi, a^m signifie que la quantité « doit être élevée à une puissance quelconque m, c'est-à-dire être m fois facteur, et se prononce a puissance m.

Quand on veut indiquer la puissance d'un polynôme, on le renferme entre deux parenthèses, et l'on place l’exposant en dehors et en haut de la dernière parenthèse ; ainsi (a + b – c ) ³ indique le cube ou la 3^e puissance du trinôme a + b — c,

· De quelques formules fréquemment employées ( voir @ les identités remarquables)

La multiplication des binômes de la forme et par eux-mêmes, c'est-à-dire leur carré, donne lieu à des formules qu'il est indispensable de retenir. Nous allons les donner ici.

a	+ b		a	- b
a	+ b		a	- b
a²	+ ab		a²	- ab
	+ ab	+ b²		- ab	+ b²
a²	+ 2 ab	+ b²	a²	-2 ab	+ b²

Ces opérations peuvent évidemment s'écrire ainsi :.

(a + b )² = a² + 2ab + b²

Ce premier résultat nous apprend qu'en général le carré de la somme de deux quantités contient :

Le carré de la première, plus deux fois le produit de la première par la seconde, plus le carré de la seconde.

(a — b)² = a ² — 2ab + b².

Ce second résultat indique que le carré de la différence de deux quantités contient :

Le carré de la première moins deux fois le produit de la première par la seconde, puis le carré de la seconde.

Remarquons que le carré d'un binôme, quels que soient les signes de ses termes, est toujours composé de trois termes dont le premier a² et le dernier b² ,toujours positifs, sont les carrés respectifs des deux termes du binôme proposé, et dont le second + 2ab ou — 2 ab est le double produit de ces mêmes termes pris avec le signe + . Si les deux termes du binôme ont le même signe, et avec le signe — s'ils sont de signes contraires.

· Il résulte encore de là qu'un binôme ne peut jamais être un carré, parce que le carré d'un monôme est un monôme, et que le carré d'un binôme est un trinôme.

· Proposons-nous maintenant d'effectuer le produit de la somme de deux quantités a + b par leur différence a — b ; nous aurons

a	+ b
a	- b
a²	+ ab
	- ab	- b²
a²	0 ab	- b²

Ce résultat a² — b² annonce que le produit de la somme de deux quantités par leur différence est égal à la différence des carrés de ces quantités.

Réciproquement :

La différence de deux carrés pourra toujours être considérée comme provenant du produit de la somme par la différence des deux racines ; ainsi m² - n² = (m+ n)(m – m ).

Cette décomposition de la différence do deux carrés en ses facteurs binômes trouve une foule d'applications utiles.