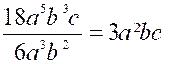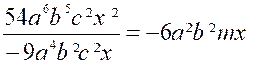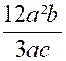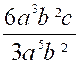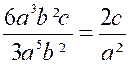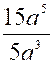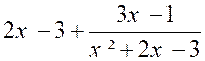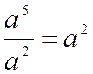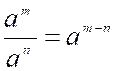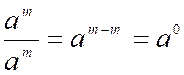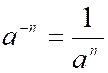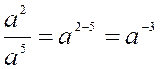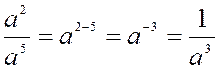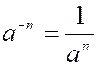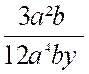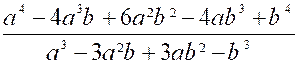1°) Division de monômes .

2°) Division de polynômes .

3°) De l'exposant zéro et de l'exposant négatif.

Nous avons déjà vu comment on indique, par signes, l'addition, la soustraction, la multiplication division des quantités algébriques, et c'est l'emploi de  ces signes qui a donné naissance aux expressions littérales   que nous avons appelées monômes et polynômes . Mais ces quantités littérales elles-mêmes, avec leurs signes, leurs lettres, leurs coefficients et leurs exposants  sont soumises à leur tour aux quatre opérations fondamentales, d'après des règles qui constituent le calcul  algébrique.

Ces opérations rappellent en général  les mêmes idées qu'en arithmétique, et comportent les mêmes définitions.

La division   algébrique

Le but de la division, en algèbre comme en arithmétique, est toujours celui-ci : étant donnés le produit de deux facteurs et l'un de ces facteurs, trouver l'autre facteur. Donc, pour arriver à la prati­que et à la théorie de la division algébrique, il i'aut se rappeler les lois que nous avons établies ci-dessus dans la multiplication algébrique.

I )  Division des monômes,

Proposons-nous, par exemple, de diviser 18a ⁵ b ³c par  6 a ³  b² ;   je dis que nous aurons pour quotient ce qu'on exprime ainsi :

Démonstration. En effet, d'après la définition ci-dessus, le dividende 18a ⁵ b ³c  est le produit du diviseur 18a ⁵ b ³c par le quotient demandé; or, d'après les règles de la multiplication des monômes, le signe, le coefficient, les lettres et les exposants du produit dépendent de ceux des deux facteurs, et, en se rappelant ces règles, on en tirera les déductions suivantes •.

1° Le produit 18a ⁵ b ³c  étant positif, les deux facteurs qui l'ont formé sont de même signe (revoir règle des signes); donc le quotient sera positif comme le diviseur 6 a ³  b²

2° Le coefficient 18 du dividende étant formé (revoir la règle des coefficients ) de la multiplication du coefficient 6 du diviseur par le coefficient inconnu du quotient, ce dernier s'obtiendra en divisant 18 par 6, et sera 3. . 3» L'exposant 5 de la lettre  « a »  dans le dividende provient (revoir la règle des exposants)) de l'addition de l'exposant 3 de  « a »  du diviseur à l'exposant inconnu de la même lettre dans le quotient ; on aura donc 5 — 3 = 2 pour l'expo­sant de « a »   au quotient.

Par la même raison, b ³ du dividende, divisé par  b ² du diviseur, donnera au quotient b ^{3 – 2}  = b ¹ = b.

4° Enfin, la lettre c (revoir la règle des lettres ), qui se trouve au divi­dende sans être dans le diviseur, doit se trouver telle quelle au quotient.

Cette démonstration conduit aux règles suivantes pour la division des monômes.

Règle des signes. Quand le dividende et le divi­seur ont même signe, le quotient est positif; si le dividende et le diviseur sont de signes contraires, le quotient est négatif.

Règle des coefficients. Le coefficient du quotient s'obtient en divisant le coefficient du dividende par celui du diviseur.

Règle des exposants. Pour chaque lettre com­mune aux deux facteurs, on forme l'exposant du quotient en retranchant l'exposant du diviseur de celui du dividende.

Règle des lettres.

1°)  Toute lettre qui se trouve au dividende et au diviseur avec le même exposant ne fait point partie du quotient ;

2°)  Une lettre qui est au dividende sans être au diviseur sera écrite telle quelle au quotient.

Pour l'application de ces règles, soit à diviser   54 a ⁶ b ⁵ c² m x²  par  - 9 a⁴ b² c² x

On aura :

 (Voir les exercices  ci-dessous )

Diviser        72 a ⁵ b³  par  9 a³b

Diviser        35 a ³ b² c par – 7 a² c

Diviser      - 48 a ⁷ b ⁵ c² x  par  12 a⁴ b ³ x

Diviser      - 56 a ⁹ b ⁷ c³ x² par – 8 a⁵ b³c³

Remarque. Il suit des règles précédentes, qui ne sont qu'une conséquence de celles de la multiplication  que la division algébrique entre deux monômes est impossible

1°)  Quand le diviseur contient une ou plu­sieurs lettres qui ne fout pas partie du dividende;

    2°)  Quand une lettre, commune aux deux termes, a dans le diviseur un exposant plus fort que dans le dividende.

Ainsi 12a² b   n'est pas divisible par 3 ac; de même la division de 6a³ b ² c par 3a⁵ b ² est impossible.

Dans ces cas on se borne à indiquer la division, en mettant l'expression sous forme fractionnaire, comme ci-après :

       et         ;

mais il convient de simplifier les fractions algébriques, comme les fractions arithmétiques, en supprimant les facteurs qui sont communs aux deux termes de la frac­tion; ainsi, 3a étant commun aux deux termes de la

fraction   celle-ci se réduit à           ;

de même, 3a³b²   divisant les deux termes de la fraction , on aura

Division des polynômes .

II )  Division de polynômes

Le mécanisme de la division algébrique des poly­nômes a beaucoup d'analogie avec celui de la division d'un nombre entier par un. autre, et se réduit à la règle suivante :

règle. Pour diviser un polynôme par un autre, com­mencez par les ordonner tous les deux par rapport à la même lettre, et ensuite divisez le premier terme du di­vidende par le premier terme du diviseur, d'après les règles de la  division des monômes exposées ci-dessus, et ce quotient monôme sera le premier terme du quotient demandé ; alors multipliez tous lés termes du diviseur par ce premier terme du quotient, et retranchez le pro­duit obtenu du dividende. Pour opérer commodément cette soustraction, on écrit sous le dividende les produits partiels de chaque terme du diviseur par le premier terme du quotient, à mesure qu'on les forme et en ayant soin de changer leurs signes, de sorte qu'il ne reste plus qu'à effectuer la réduction.

Cette première opération conduit à un premier reste qui sera en général ordonné comme les polynômes pro­posés, mais que l'on ordonnerait s'il ne l'était pas ; ce reste constitue alors le premier dividende partiel; Cela posé, on divisera encore le premier terme de ce reste par' le premier ternie du diviseur, et cette seconde divi­sion monôme donnera le second terme du quotient. Alors on fera le produit du diviseur tout entier par ce second ternie du quotient pour le retrancher du premier divi­dende partiel, afin d'obtenir pour reste un second divi­dende partiel, et l'opération continuera ainsi tant que le premier terme des restes successivement obtenus sera divisible par le premier terme du diviseur. Par le fait, ce premier terme est le seul diviseur actif.

L'application de cette règle à l'exemple suivant la fera mieux comprendre :

Soit à diviser : – 4 b ⁵  + 60 a³ b²– 61 a ⁴b +15 a ⁵- 5 a² b³ – 35 a b⁴  par + 4 b³+ 5 a ³+ 3 a b²– 7 a² b

(revoir : la multiplication de polynôme) ).

On ordonnera d'abord ces deux polynômes d'après les puissances décroissantes de a, et on les disposera comme il suit :

15 a ⁵ – 61 a ⁴b + 60 a³ b² - 5 a² b³ – 35 a b⁴ – 4 b ⁵  divisé par  5 a ³ – 7 a² b + 3 a b² + 4 b³

En divisant le 1^er  terme  15 a ³ du dividende par le 1^er  terme 5 a ³  du diviseur, on a eu 3 a²  pour le 1^er  terme du quotient, lequel, multiplié par tous les termes du diviseur, donne pour produit 15a⁵—21a⁴b + 9a³b ² +  12a²b ³; ce produit, écrit avec des signes contraires sous le dividende, a fourni, par la réduction des termes semblables, le 1^er  reste — 40 a⁴ b + 51 a ³ b²  , etc.  qui devient le premier dividende partiel or­donné.

Ensuite on a divisé le premier terme — 40 a⁴  de ce reste par le pre­mier terme 5 a ³   du diviseur  , et le quotient mo­nôme — 8ab, écrit au quotient, a formé son se­cond terme. Le produit de ce second terme du quotient   par tous   les termes du  diviseur, et pris en signes contraires, a été écrit sous le divi­dende pour en opérer la soustraction, et toute ré­duction faite, on a trouvé le   deuxième reste   or­donné— 5 a³b⁸ + 7a² b³ — etc ......... qui est devenu le second dividende partiel.

De même, la division monôme du premier ter­me — 5a³b²  de ce 2^e reste par le premier ter­me 5a³ du diviseur a fourni le 3^e terme du quotient — b².

 Enfin le produit de — b² par tous les termes du divi­seur , écrit en signes contraires sous le 2^e dividende partiel, ayant donné zéro pour reste, on en conclut que la division est terminée et que le quotient est exact.

Démonstration. La théorie de la division, comme nous l'avons dit, se déduit des règles de la multiplica­tion. Ainsi, en considérant le dividende comme le, produit réduit du diviseur par le quotient, et supposant ces trois polynômes ordonnés par rapport à la même lettre, on voit clairement (revoir les multiplications de polynômes) que le premier terme 15a⁵ du dividende est le produit sans réduction du premier terme 5a³ du diviseur par le premier terme inconnu du quotient .- ainsi la division monôme    donne nécessairement ce 1^er  terme 3a² du quotient.

Le 1^er   terme obtenu, il est nécessaire de le multiplier par le diviseur et de retrancher le produit du dividende pour débarrasser ce dernier de ce qui est devenu inu­tile .'Mais observons que si le dividende est le produit du diviseur par le quotient, comme nous l'admettons, les réductions qu'on a dû opérer antérieurement ont fait disparaître des termes qui ne figurent plus dans ce dividende et dont il faut tenir compte ; aussi la multipli­cation de chaque terme du quotient par tous les termes du diviseur a-t-elle pour effet de remettre en évidence les termes semblables réduits, comme on le voit en comparant les calculs ci-dessous à ceux du produit des polynômes .

Quand on est arrivé au 1^er  reste — 40 a⁴ b + 51 a ³ b²  , etc.  , on doit le considérer comme le produit du diviseur par tous les ternies qui manquent au quotient ; mais, dans ce produit, le premier terme 5a³ du diviseur, multiplié par le second terme du quotient, donnera un monôme dans lequel la lettre principale a aura un exposant plus élevé que dans tous les autres produits partiels ; en conséquence, ce monôme ne peut être que le premier terme — 40 a⁴ b du reste obtenu pour premier divi­dende partiel; donc — 40 a⁴ b divisé par 5a³, donnera le second terme du quotient — 8ab

Calculs :

15 a ⁵

– 61 a ⁴b

+ 60 a³ b²

- 5 a² b³

– 35 a b⁴

– 4 b ⁵

5 a ³

– 7 a² b

+ 3 a b²

+ 4 b³

(produit 1 )

- 15 a ⁵

+ 21 a ⁴b

- 9 a³ b²

- 12  a² b³

3 a²

- 8 ab

- b²

Quotient

Premier reste

0

+ 40 a ⁴b

+ 51  a³ b²

- 17  a² b³

– 35 a b⁴

– 4 b ⁵

(Produit 2)

-40 a ⁴b

-  56  a³ b²

+ 24 a² b³

+ 32 a b⁴

2^ème reste

0

-  5  a³ b²

+ 7  a² b³

+ 3 a b⁴

– 4 b ⁵

(Produit 3 )

+   5  a³ b²

-  7  a² b³

-  3 a b⁴

+  4 b ⁵

Reste

0

0

0

0

Le même raisonnement conduira à diviser le 1^er  terme — 5 a³ b ² du second reste par le premier terme 5a³ du diviseur, pour avoir le 3^ème  terme du quotient, et il en serait ainsi, quelque nombre de termes qu'on dût obtenir au quotient.

Remarque I. Nous avons admis que le dividende était le. produit réel du diviseur par le quotient', parce que c'était nécessaire à la théorie, et qu'alors seulement l'opération conduit à un quotient exact et à un reste zéro ; mais dans bien des cas il n'en est pas ainsi, et pour les polynômes comme pour les monômes et pour les nom­bres, on peut avoir à diviser un polynôme par un autre qui n'en soit pas facteur exact ; alors le quotient est incomplet et la division donne un reste. Cependant on procède toujours d'après la règle ci-dessus.

Soit, pour exemple,  2 x³ + x² - 9 x + 8  diviser par x² + 2 x – 3 ; nous aurons :

2 x³

x²

- 9x

+8

 x²

2x

-3

(produit 1 )

- 2 x³

- 4 x²

+ 6 x

2 x

- 3

Premier reste

0

- 3 x²

- 3 x

+8

(Produit 2)

+  3 x²

+ 6 x

- 9

reste

………..

3 x

- 1

Après deux opérations partielles nous obtenons un reste 3x — 1 dans lequel x   a un exposant inférieur à celui de la même lettre dans le premier terme x²  du diviseur; dès lors l'opération ne peut plus s'effectuer (voir la remarque précédente ), et le quotient 2 x  — 3 est incomplet. Dans ce cas on peut mettre le reste sous forme de fraction, et le quotient demandé devient  

Remarque II. Les principes vu en début de cours  nous feront connaître, à l'inspection des polynômes et des restes suc­cessifs, si la division est impossible ; mais rien ne peut à l'avance servir de guide pour déterminer le nombre de ternes que  contiendra le quotient d'une division algébrique, parce qu'on ne saurait prévoir les réductions qui ont pu être opérées antérieurement. (Voir les exercices nos 80 à 88.)

Info plus

III ) De l'exposant zéro et de l'exposant négatif.

La division algébrique donne naissance à certaines quantités qui ont besoin d'une interprétation particu­lière : ce sont les expressions a° et a ^{– n ,} que nous allons examiner,

Toute lettre affectée de l'exposant zéro repré­sente l'unité, c'est-à-dire qu'on aura toujours

a° = 1.

. En effet, la règle de l’exposant établit  en début du cours que l'on doit retran­cher l'exposant du diviseur de celui du dividende pour avoir l'exposant du quotient, c'est-à-dire que

   , et qu'en général  

Dans ce quotient les exposants m, n du dividende et du diviseur peuvent être quelconques et quelquefois égaux; or, lorsqu'on aura m = n, l'expression ci-dessus deviendra   

mais, dans tous les cas, une quantité quelconque a ^m  , divisée par elle-même, ne peut donner que l'unité pour quotient; donc a ⁰ = 1.

Exposant  négatif   : Toute lettre affectée d'un exposant négatif représente une fraction dont le numérateur est l'unité, et qui a pour dénominateur cette même lettre avec son exposant positif; ainsi :

a-³  =   , et en général  

En effet, d'après l'observation faite ci-dessus, dans  l'expression générale   ,  on peut avoir  n > m , comme dans l'exemple      et l'on obtient un exposant négatif.

 Mais la fraction   ayant un facteur a ²  commun à ses deux termes,est susceptible  de simplification, et devient par là  donc enfin et en général

( Voir les exercices n^os 90 à 93.)

Diviser        72 a ⁵ b³  par  9 a³b

Diviser        35 a ³ b² c par – 7 a² c

Diviser      - 48 a ⁷ b ⁵ c² x  par  12 a⁴ b ³ x

Diviser      - 56 a ⁹ b ⁷ c³ x² par – 8 a⁵ b³c³

La division de 36 a³ b³ c par – 8 a² b² x est – elle possible ?

Simplifier l’expression fractionnaire qui résulte de l’exercice précédent .

Simplifier la fraction

Diviser  a³ + a ² – 29 a par  2 a - 3

Trouver le quotient de x⁴ – 9 b² x² -  6 b c² x – c⁴  par x² – 3 b x – c²

Diviser  a⁶ + 2³ y³ + y ⁶ par a² - ay + y²

Effectuer  la division :

Diviser 8 a⁴ b – 2 a³b²+ 4 a²b³par – 4 a² b .

Chercher le quotient de a⁵ – b⁵  par  a- b .

Exprimer en général le  quotient de a^m  - b^m  par a – b .

Diviser le polynôme 25 x² y³ + 21 x³ y²+ 68 xy⁴- 40 y⁵-56 x⁵ – 18 x⁴y  par le polynôme 5 y²-8x²- 6 xy

Chercher le quotient de 12 a x ⁵ – 9 a²x⁴ + 5 a³ x par  4 ax² 3 a²x

Diviser 14 a⁵ – 27 a⁴b + 21 a³ b² + 3 a² b³ – 2b ⁴par 2 a² - 3ab + 2 b²

A  quoi sont équivalentes les expressions : a⁰  et b⁰

A quoi se réduit l’expression : 

Trouver la valeur de a ^-2  pour a = 8

21. 

Transformer   la valeur x = a ^-3 ( a – b) ^-2  en une expression équivalente.

22.               

Que devient cette valeur de x si l’on fait a= 5 et b = 3