|
Auteur :
WARME R.
DOCUMENT ELEVE.
|
||
|
NOM :
|
Prénom :
.. |
Classe :
.. |
|
Année scolaire :
|
Dossier
pris le :
/
/
|
Validation
de la formation : O -
N Le :
.. Nom
du formateur :
|
|
ETABLISSEMENT :
.. |
||
|
Leçon |
Titre |
|||
|
N°3 |
LES QUATRE
OPERATIONS dans D |
|||
|
CHAPITRES |
||||
|
1°)ADDITION |
||||
|
2°)
SOUTRACTION |
||||
|
4°)DIVISION |
||||
|
|
|
|||
|
COURS |
||||
|
1- ADDITION |
||||
|
|
Définition : Laddition est une opération qui permet dajouter ( faire la somme) des éléments de même nature. Le résultat
dune addition sappelle une somme. |
|
|
|
iOn ajoute
des mètres avec des mètres, des mètres carrés avec des mètres carrés,
..etc.
Exemple :
Calculer 152 + 13,52 + 8 125,3 + 10
345,612 = ?
|
|
|
Nota : On peut compléter par des « 0 » les décimaux les
plus courts pour avoir le même nombre de
chiffres après la virgule . |
1 5 2
, 0 0 0 + 1 3 , 5 2 0 + 8 1 2 5 , 3 0 0 + 1 0 3 4 5 , 6 1 2 __________________ 1 8 6 3 6 , 4 3 2 |
|
|
Propriétés
de laddition : ( Info
plus : les propriétés de
laddition) |
|
|
On peut
changer lordre des termes ; on ne change pas la valeur du résultat |
||
|
|
Exemple : 32,4 +
6,2 + 43,57 = 82,17 ; 6,2 + 32,4 + 43,57 =
82,17 |
|
|
On peut remplacer
plusieurs termes dune addition par leur somme effectuée et ensuite
additionner ces sommes ; on ne change pas la valeur du résultat. |
||
|
|
Exemple :
32,4 + 6,2 + 43, 57
= 82,17 car 32,4 + 6,2 =
38,6 et 38,6 + 43,57 = 82,17 iOn peut utiliser ces propriétés pour vérifier lexactitude
du résultat . |
|
|
2- SOUSTRACTION |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Définition : La soustraction est une opération qui permet de retrancher (ôter) un terme à un autre
de même nature. On pose le plus grand et on lui soustrait le plus petit. Le
résultat dune soustraction sappelle la différence. |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
iComme
pour laddition, lorsque lon pose lopération, il faut respecter lalignement des chiffres de même rang (ordre) ainsi que les
virgules. |
|
||||||||||||||||||||||||||||||||||||||||||||
|
Exemple :
3 782,25 435,5 = ? Nota : il est conseillé de compléter , la partie décimale
des nombres décimaux les plus courts , par des « 0 » pour avoir le même nombre de chiffres
après la virgule . |
3 7
8 2 ,
2 5 (le plus
grand nombre) - 4 3 5
, 5 0
(le plus petit nombre) ___________ 3 3
2 8 , 7 5 |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
iDans une soustraction , il faut respecter
lordre des termes : on soustrait
toujours le plus petit au plus grand , sinon lopération est impossible. |
|
||||||||||||||||||||||||||||||||||||||||||||
|
Vérification du résultat dune soustraction ( Info
plus :la preuve par neuf) |
||||||||||||||||||||||||||||||||||||||||||||||
|
a)Additionner le résultat avec le nombre que lon a
soustrait et retrouver le nombre de départ. |
15 -
7 = 8
« vraie » si 7 +
8 = 15 |
|||||||||||||||||||||||||||||||||||||||||||||
|
b)Soustraire le résultat au nombre de départ et retrouver
et retrouver le nombre que lon a soustrait. |
12 - 5
= 7
« vraie » si 12 7 =
5 |
|||||||||||||||||||||||||||||||||||||||||||||
|
Pré
requis : i29 |
||||||||||||||||||||||||||||||||||||||||||||||
|
3 - MULTIPLICATION cas particuliers : le carré d'un nombre
et le cube d'un nombre |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Définition : Opération associant
deux nombres lun appelé multiplicande lautre appelé multiplicateur. Le
résultat de lopération est appelé produit |
|
||||||||||||||||||||||||||||||||||||||||||||
|
iLorsque
lon additionne plusieurs termes identiques, on peut effectuer une
multiplication |
||||||||||||||||||||||||||||||||||||||||||||||
|
Exemple : 14 + 14 + 14 =
14 |
||||||||||||||||||||||||||||||||||||||||||||||
|
Produit
de deux nombres décimaux Exemple : 42,3 On effectue
lopération comme avec des nombres
entiers et on placera la virgule après
avoir obtenu le résultat. |
||||||||||||||||||||||||||||||||||||||||||||||
|
On ne tient pas compte de la virgule au moment de
lopération. On compte le nombre de chiffres des parties décimales et on place la
virgule dans le résultat au même
nombre de rangs en partant de la
droite . Si le résultat se
termine par un ou plusieurs « 0 » , on tient compte de ces
« 0 » pour le positionnement de la virgule . |
4 2 , 3 __________ 1 6 9 2 0
0 0
· 4 2 3 · · __________ 4 3
9 9 2 « 3 chiffres après la virgule » : on
placera la virgule à3 rangs en partant de la droite. 42,3 |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
iDans le
calcul dun produit , on peut changer lordre des nombres , ou regrouper
plusieurs nombres |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
Exemples a) 4,5 |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
b) 2 |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
Le
« Carré » d'un nombre
: le produit d'un
nombre par lui -même s'appelle le
"carré d'un nombre" : (exemple : 36 est le produit de
6 ( on retiendra que : Le
« carré » dun nombre entier
est appelé « carré
parfait ». |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
Le
« Cube » d'un nombre
: le produit d'un nombre
par lui -même , par lui -même s'appelle le "cube d'un nombre" :
(exemple : 27 est le produit de 3 Application : Le volume dun cube de 6 cm darête est
égal à ( 6 cm )3 soit
216 cm3 |
|
||||||||||||||||||||||||||||||||||||||||||||
|
RENDRE UN NOMBRE 10 ;100 ;1000 fois plus grand ou plus
petit . |
Cd : revoir le
cours sur : Multiplier par 10 ;100 ;1000 |
|||||||||||||||||||||||||||||||||||||||||||||
|
a) Rendre 10 ; 100 ; 1000 plus
petit Pour rendre un nombre
décimal 10 ; 100 ; 1000 ;
fois plus petit , on avance (
déplace) la virgule vers la gauche de 1
rang , de 2 , de 3 ; etc . rangs. Exemple
: Le nombre
456,7 rendu 100 fois plus petit
devient : 4,567 |
||||||||||||||||||||||||||||||||||||||||||||||
|
b) Rendre 10 ; 100 ; 1000
plus grand On rend un nombre
décimal 10 ; 100 ; 1000 ;
fois plus grand en avançant la
virgule (
..,..
) de 1 ; 2 ; 3 ; rangs vers la droite . Exemple le nombre 28,76 rendu 10 fois plus grand
devient 287,6 |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
Pré requis : i29 et la division en primaire. i39 |
||||||||||||||||||||||||||||||||||||||||||||||
|
4- DIVISION |
||||||||||||||||||||||||||||||||||||||||||||||
|
Définition : On effectue une division lorsque lon veut effectuer un partage. Par
exemple lorsque lon cherche la valeur dune part ou lorsque lon cherche le
nombre de part Le
résultat de la division sappelle le Quotient |
||||||||||||||||||||||||||||||||||||||||||||||
|
Exemple :
162 : 3 = 54 ( 162 est appelé
« dividende » ; «3 » est appelé
« diviseur » ; « 54 » est appelé
« quotient ») . Pour diviser des
nombres décimaux , on doit savoir
faire la division avec des nombres entiers.( On passe par la division des
nombres entiers( dit :
division euclidienne)) . Exemple : 3427 ¸ 12 = ( 3427 est appelé : « Dividende » , 12 est le « diviseur » ) (il faut écrire la table du
diviseur : la table des 12 . |
||||||||||||||||||||||||||||||||||||||||||||||
|
DIVISION DE DEUX NOMBRES ENTIERS |
||||||||||||||||||||||||||||||||||||||||||||||
|
On peut
arrêter la division lorsquon a abaissé tous les chiffres du dividende. On
pose la table du diviseur : 1 ´ 12 = 12 2 ´ 12 = 24 3 ´ 12 = 36 4 ´ 12 = 48 5 ´ 12 = 60 6 ´ 12 = 72 7 ´ 12 =84 8 ´ 12 = 96 9 ´ 12 = 108 285 est
alors le quotient et 7 est le reste.. . |
|
3 |
4 |
2 |
7 |
|
1 |
2 |
|
|
||||||||||||||||||||||||||||||||||||
|
- |
2 |
4 |
¯ |
|
|
2 |
8 |
5 |
|
|||||||||||||||||||||||||||||||||||||
|
|
1 |
0 |
2 |
¯ |
|
|
(« 285 » est le
quotient) |
|||||||||||||||||||||||||||||||||||||||
|
- |
|
9 |
6 |
¯ |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
0 |
6 |
7 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
- |
6 |
0 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
(reste : 7 ) |
|
7 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
Si
lon veut continuer la division , il faut
alors mettre une virgule au quotient et abaisser un « O » à la
droite du « 7 » .( reste) |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Règle 1: Division
dun nombre décimal par un nombre entier |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Lorsque le dividende est un nombre décimal : on met
la virgule au quotient lorsque lon abaisse le chiffre des
« dixièmes » Ou bien ,on peut supprimer
la virgule du dividende en le multipliant par 10 ; 100 ;
1000 ; il faut alors multiplier le diviseur par la même valeur . Règle 2 : Division
de nombres décimaux Lorsque le diviseur est un nombre décimal ,
on peut supprimer la virgule en le multipliant par 10 ; 100 ;
1000 ; il faut alors multiplier le dividende par la même valeur . On retiendra aussi que : le résultat de la division
sappelle : le quotient |
||||||||||||||||||||||||||||||||||||||||||||||
|
Exemple : Diviser : 53763,
2 : 2, 3 jusque
2 chiffres après la virgule ; |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
PROCEDURE pour diviser deux nombres décimaux |
||||||||||||||||||||||||||||||||||||||||||||||
|
1°) Mettre la division sous forme décriture fractionnaire
|
53763 , 2 : 2
, 3 = |
|||||||||||||||||||||||||||||||||||||||||||||
|
2°) Transformer lécriture fractionnaire en fraction . ( on
multiplie par 10 en haut et en bas ,
on obtient une fraction équivalente à
lécriture fractionnaire ) |
(Respecter lordre décimal! ! ! !)
|
|||||||||||||||||||||||||||||||||||||||||||||
|
3°) Poser la division : « euclidienne » On doit
diviser un nombre entier «
537632 » par le nombre entier « 32 » |
5 3 7 6 3 2 ,0
0 ½
23 ½ --------- ½ ½ |
|||||||||||||||||||||||||||||||||||||||||||||
|
Commentaire : Pour effectuer la division, on doit savoir établir
« mentalement »la table de multiplication du diviseur
« 23 ». Si vous
avez des difficultés en calcul mental
il est conseiller décrire sur la feuille de papier cette table. |
0 fois 23 = 0 1 fois 23 = 23 2 fois 23 = 46 3 fois 23 = 69 4 fois 23 = 92 5 fois 23 = 115 6 fois 23 = 138 7 fois 23 = 161 8 fois 23 = 184 9 fois 23 = 207 |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
5 |
3 |
7 |
6 |
3 |
2 |
, |
0 |
0 |
|
2 |
3 |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
- |
4 |
6 |
|
|
|
|
, |
|
|
|
2 3 3 7 5,
3 0 |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
0 |
7 |
7 |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
- |
6 |
9 |
|
|
|
, |
|
|
|
|
|
Pour vérifier ce quotient il faut multiplier : 23 375 , 30 par 23 et ensuite ajouter le reste ; on doit retrouver le nombre : 537632. |
|
|||||||||||||||||||||||||||||||
|
|
|
|
0 |
8 |
6 |
|
|
, |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
- |
6 |
9 |
|
|
, |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
7 |
3 |
|
, |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
- |
1 |
6 |
1 |
|
, |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
0 |
1 |
2 |
2 |
, |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
- |
1 |
1 |
5 |
, |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
0 |
0 |
7 |
, |
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
- |
6 |
, |
9 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
, |
1 |
0 |
|
|
|
|
Reste
0,1 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
Conclusion :
5376 , 32 : 2 , 3 » 2 3
3 7 5, 3 0 à deux décimales |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
Exemple 2 : Diviser
76,528 : 4,21 ( on demande d exprimer le résultat à 0,01 près .) |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
PROCEDURE pour diviser deux nombres décimaux |
||||||||||||||||||||||||||||||||||||||||||||||
|
1°) on
transforme la division en écriture fractionnaire |
76,528 :
4,21 = |
|||||||||||||||||||||||||||||||||||||||||||||
|
2°)on
transforme lécriture fractionnaire en
fraction équivalente dont le numérateur et le dénominateur sont
des nombres entiers.: |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
3°)On
établit la table de multiplication de
« 4210 » |
0
fois 4210 = 0 1 fois
4210 = 4210 2
fois 4210 = 8420 3
fois 4210 = 12630 4
fois 4210 = 16 840 5
fois 4210 = 21
050 6
fois 4210 = 25
260 7
fois 4210 = 29
470 8
fois 4210 = 33680 9
fois 4210 = 37
890 |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
On met la virgule au quotient |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
7 |
6 |
5 |
2 |
8 |
, |
0 |
0 |
0 |
|
|
4 |
2 |
1 |
0 |
|
|
|
|
|
|
- |
4 |
2 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
3 |
4 |
4 |
2 |
8 |
|
|
|
|
|
|
1 8 , 1 7 7 |
|
|
|
|
||||
|
- |
3 |
3 |
6 |
8 |
0 |
|
¯ |
|
|
|
|
|
|
|
Pour vérifier ce quotient il faut multiplier : 18,17 7 par 4210 et ensuite ajouter le reste ; 2,83 on doit retrouver le nombre : |
|||||
|
|
0 |
0 |
7 |
4 |
8 |
|
0 |
|
|
|
|
|
|
|
||||||
|
|
|
- |
4 |
2 |
1 |
|
0 |
¯ |
|
|
|
|
|
|
||||||
|
|
|
|
3 |
2 |
7 |
|
0 |
0 |
|
|
|
|
|
|
||||||
|
|
|
- |
2 |
9 |
4 |
|
7 |
0 |
¯ |
|
|
|
|
|
||||||
|
|
|
|
0 |
3 |
2 |
|
3 |
0 |
0 |
|
|
|
|
|
||||||
|
|
|
|
- |
2 |
9 |
|
4 |
7 |
0 |
|
|
|
|
|
||||||
|
Reste : |
|
0 |
2 |
, |
8 |
3 |
0 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Reste : 2 , 830 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
On conclura : 76, 528 : 4,21 » 18,18
; le résultat est arrondi « à deux décimales prés » Vérification : Est-
ce que 76,528 est égal à (18, 177 ´ 4,21) + 2,830
= ? =
si oui la division est « bonne » |
||||||||||||||||||||
|
Leçon |
|
|
N°3 |
TRAVAUX
d AUTO - FORMATION sur LES QUATRE
OPERATIONS |
Compléter
les phrases suivantes : avec les mots suivants :
« quotient » ;
« produit » ; « ajouter » ; « différence » ;
« somme » ;
« retrancher » (ôter) ;
« multiplication » ; « partage » ;
« petit » ; « grand » .
1°) Laddition est une opération qui permet d
( faire la somme) des éléments de même nature .
Le résultat dune addition s appelle :
.
2°) La soustraction est une opération qui permet de
un terme à un autre de même
nature .
On pose le plus
. et on lui soustrait le
plus
. .
le résultat dune soustraction sappelle : la
3°) Lorsque lon
additionne plusieurs termes identiques , on peut effectuer une
..
Le résultat dune multiplication sappelle : le
.
4°) On effectue une division
lorsque lon veut effectuer un
. .
le résultat de la division sappelle le
..
TRAVAUX
N°3 AUTO - FORMATION EVALUATION
Exercices :
N°1 : Effectuer les
additions suivantes :
|
2 078 +
986 = |
|
|
100 + 37,45 = |
|
|
42,85 + 34,56 = |
|
|
3 265 , 63 + 1052 ,72 = |
|
N°2 : Effectuer les
soustractions suivantes :
|
2 078 -
986 = |
|
|
100 37,45 = |
|
|
42,85 34,56 = |
|
|
3 265 , 63 1052 ,72 = |
|
N°3 : Poser et
effectuer les multiplication suivantes :
|
134 |
|
|
31,7 |
|
|
352 |
|
|
0,605 |
|
|
53,01 |
|
|
42,3 |
|
N°4 : Poser et
effectuer les divisions suivantes :
|
134
: 16 = |
|
|
31,7 : 42 =
à 1 décimale |
|
|
352 : 0,93 =
( à 0,01 près) |
|
|
0,605 : 9,71 = ( à 0,001 près) |
|
|
53,01 : 0,04 = |
|
Série 2 : rendre un nombre 10 ; 100 ; 1000 fois plus grand ;
N°5 : compléter
|
¯ ¬ |
7 |
1,3 |
25,68 |
10 |
|
|
|
|
|
N°6 : compléter
|
¯ ¬ |
500 |
851,379 |
268 |
49 |
|
|
|
|
|
N°8 : compléter
|
¯ ¬ |
2 |
1,3 |
25,68 |
421,54 |
|
|
|
|
|
N°9 : compléter
|
¯ ¬ |
70 |
300 |
125,068 |
9 |
|
|
|
|
|
N°10 : compléter
|
¯ ¬ |
07 |
31,3 |
0,02568 |
17 |
|
|
|
|
|
N°11 : compléter
|
¯ ¬ |
5 |
11,35 |
100 |
63,687 |
|
|
|
|
|
Série 3 : rendre un
nombre 10 ; 100 ; 1000 fois plus petit ;
N°12 : compléter
|
¯ ¬ ¸ 10 ® |
7 |
1,3 |
25,68 |
10 |
|
|
|
|
|
N°13 : compléter
|
¯ ¬ ¸ 10 ® |
500 |
851,379 |
268 |
49 |
|
|
|
|
|
N°14 : compléter
|
¯ ¬ ¸ 100 ® |
2 |
1,3 |
25,68 |
421,54 |
|
|
|
|
|
|
|
¯ ¬ ¸ 100 ® 70 |
300 |
125,068 |
9 |
|
|
|
|
|
|
N°15 : compléter
N°16 : compléter
|
¯ ¬ ¸ 1000 ® |
07 |
31,3 |
0,02568 |
17 |
|
|
|
|
|
N°17 : compléter
|
¯ ¬ ¸
10 ® |
5 |
11,35 |
100 |
63,687 |
|
|
|
|
|
Série 4 :
compléter ( exemple 1,3 ![]() 10 = 13 ; 0,7
10 = 13 ; 0,7 ![]() 100 = 70 )
100 = 70 )
a) calculer en ligne
|
137 |
|
|
63 |
|
|
1,7 |
|
|
3, 5 |
|
|
3,59 |
|
b) idem
|
. |
|
|
. |
|
|
.. |
|
|
.. |
|
|
.. |
|
c) idem
|
13 |
|
|
6 |
|
|
1,7 |
|
|
0 ,4 |
|
|
3,14 |
|
Série 5 : compléter
|
® |
|
|
|
6,75 |
|
13,9 |
|
|
|
19,125 |
|
¬ ¸ 3 ¬ |
|
Série 6 : compléter
|
® |
|
|
|
82,8 |
|
8,4 |
|
|
|
55,125 |
|
¬ ¸ 4,5 ¬ |
|
Série 7 : compléter
|
® |
|
|
8 |
|
|
|
68,625 |
|
2,25 |
|
|
¬ ¸ 2,25 ¬ |
|
Série 8 : compléter soit par un nombre , soit par le signe ![]() ou ¸
ou ¸
|
24 ¸
.= 8 |
52 |
5
6,5 = 32,5 |
|
354 ¸
.= 59 |
3,2 |
40
.5
= 8 |
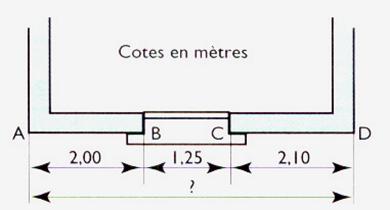
N°1 . On vous donne le plan
suivant :
|
Calculer la distance entre
les deux murs . ( côte AD) . La côte BC représente
louverture de la fenêtre . |
|
N°2 :
M .Alexis effectue des achats dans un magasin . Il achète : une veste
: 64,5 ; une chemise :
56,16 ; un pantalon : 42,46 .
Calculer le montant de la
dépense de M. Alexis .
Conclure par une phrase ,
justifiant vôtre réponse .
N°3 : M. Bernard décide de calculer le prix de revient de sa
voiture , sur lannée écoulée , (voilà un an quil a fait cette
acquisition) .
Achat : 4 567 , 56 ; réparation : 696,34
; assurance : 418,56 , carte grise : 159,90 . Quel est le prix de revient de cette
voiture .
N°4 : M. Bernard veut se rendre à la mer , il fera 440 km ( A-R) ; sa voiture consomme 6,5 l
de carburant au 100 km . Le carburant vaut 1,25 .
1. quelle quantité de carburant a- t il consommé ? 6,5( 440 : 100) = 28,6 l
2. Quel est le coût de se voyage ,en
consommation ?
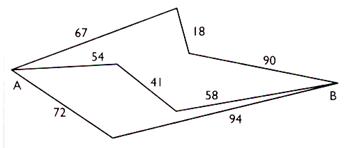
N°5
|
Pour se rendre de A à B
plusieurs possibilités sont offertes . Calculer la longueur de
ces trajets. Lequel est le plus
court ? |
|
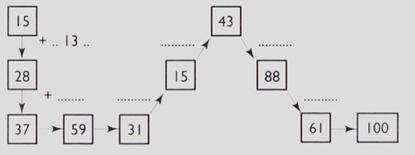
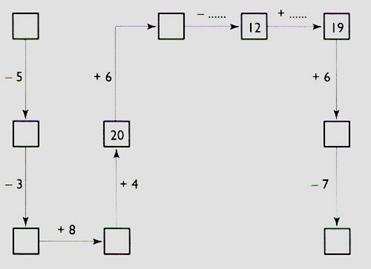
N°6 :
Compléter le cheminement
suivant :
|
|
|
N°7 :
|
Compléter le cheminement
suivant : |
|
N°8 :
Pour acheter un livre , vous
donner un billet de 50 , le libraire vous rend 37 . Quel est le
prix du livre .
N°9 : vous partez en vacances , vous devez
parcourir 650 km . Votre compteur journalier
( mis à zéro au départ) indique
« 0458 » ; quelle distance vous reste il à parcourir ?
N°10 : Dans une classe
de 35 élèves , il y a 18 garçons .
Combien y a t il de filles dans la
classe ?
N°11 : poser lopération
en ligne et écrire une phrase pour justifier la réponse.
M.Locqueneau fait le plein
dessence . IL prend 45 litres à 1,34 le litre . Combien a t il
dépensé ? 45 fois 1,34 = 60,3
N°12 : poser lopération
en ligne et écrire une phrase pour justifier la réponse.
M . Warmé fait 18 km aller retour par jour pour son
travail . Il travaille 5 jours par
semaine.
Combien fait- il de
kilomètre par semaine ?
Sachant quil travaille 45
semaine par an , combien parcours t- il de
km dans lannée pour son travail .
N° 13 . M. Truc a travaillé
35 h dans la semaine pour un
salaire net de 287,68 .Calculer le taux horaire de ce
monsieur . ( au cent dEuro près )
N°14 Pierre dépense chaque
semaine ( 5 jours) 24,6
pour manger à la cafétéria . Combien vaut un repas ?
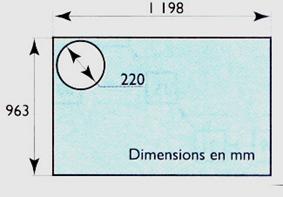
N° 15
|
On doit découper dans une
plaque de contre plaqué ( 1198 |
|
Calculer le nombre de disques
entiers que lon peut découper .
1.
dans
la longueur ?
2.
dans
la largeur ?
3.
Au
total dans cette plaque ?