|
Niveau V |
|
Pré requis:
|
|
Corrigé à
faire.. |
|
|
|
Tracé d’une perpendiculaire à une droite |
|||
ENVIRONNEMENT du dossier:
|
|
|
|
Niveau 6 : Classe 6ème-5ème |
|
Objectif précédent 1°) les
projections orthogonales 2°) L’isométrie et la rotation axiale et la symétrie axiale. 3°) ma symétrie
orthogonale ( fiche activités niveau 5 ;
collège) |
Objectif suivant
1°) Vers les
généralités sur les symétries. |
DOSSIER « LES SYMETRIES »
Fiche d’activités sur l’ axe de
SYMETRIE
|
|
Axe de symétrie d’une figure. |
|
|||||
|
|
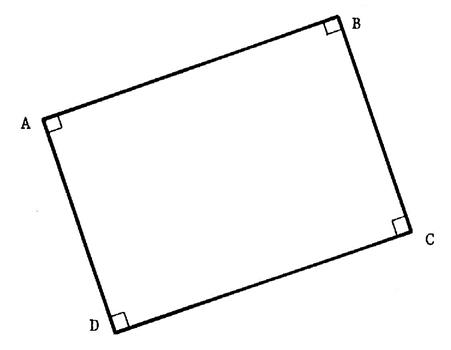
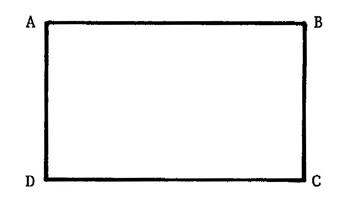
Les axes de symétrie du rectangle. |
|
|||||
|
|
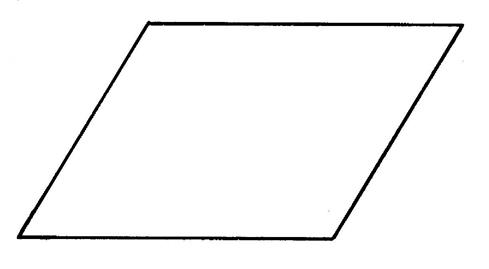
Les axes de symétrie du parallélogramme. |
|
|||||
|
|
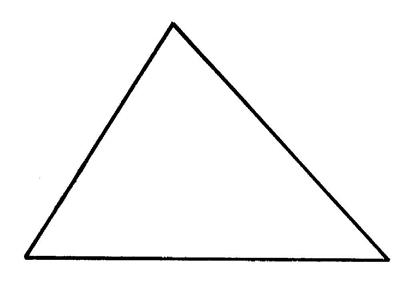
Les axes de symétrie du triangle quelconque. |
|
|||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
TEST |
COURS |
Interdisciplinarité |
|
||||
COURS :
|
|
Axe de symétrie d’une figure. |
|
|
|
|
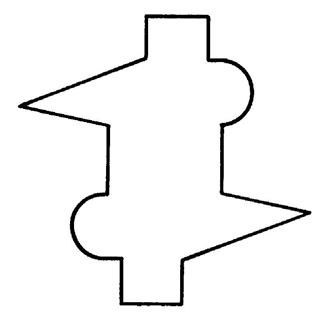
Activités …… 1°) Copiez l’image ci contre sur une feuille de
calque. 2°) Pliez la feuille de telle sorte qu’une moitié
du dessin coïncide avec l’autre moitié. 3°) Dépliez la feuille et passez au bleu la
droite de pliage , appelez « d » cette
droite. Conclusion : On dit que la figure admet
« d » comme axe de symétrie. Question : Quelle est la symétrie de cette
figure par rapport à « d » ? Rep. La symétrie orthogonale. |
|
|
|
|
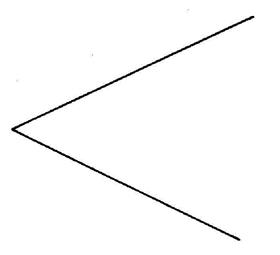
Activités …… 1°) Copiez l’image ci contre sur une feuille de
calque. 2°) Pliez la feuille de telle sorte qu’une moitié
du dessin coïncide avec l’autre moitié. 3°) Que pouvez vous
dire ?.............................on ne peut
pas superposer les demi figures. ………… Apparemment
, la figure n’a pas
d’axe de symétrie . |
|
|
|
|
A retenir : Une figure qui
admet une droite pour axe de symétrie signifie que : la
figure est sa propre symétrique par rapport à cette droite. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Activités …… 1°) Copiez l’image ci dessous sur une feuille de
calque. 2°) Pliez la feuille de telle sorte qu’une moitié
du dessin coïncide avec l’autre moitié. 3°) Dépliez la feuille et passez au bleu la
droite de pliage , appelez « d » cette
droite. |
Activités …… 1°) Copiez l’image ci dessous sur une feuille de
calque. 2°) Pliez la feuille de telle sorte qu’une moitié
du dessin coïncide avec l’autre moitié. 3°) Dépliez la feuille et passez au bleu la
droite de pliage , appelez « d » cette
droite. |
|
|
|
|
|
|
|
|
|
|
|
|
|
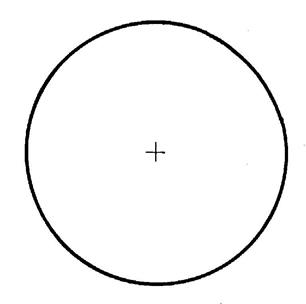
Activités …… 1°)Tracez quelques axes
de symétrie du cercle , ci contre. · Ce sont des ….diamètres. du cercle. · Combien peut-on en tracer ? ( une infinité). |
|
|
|
|
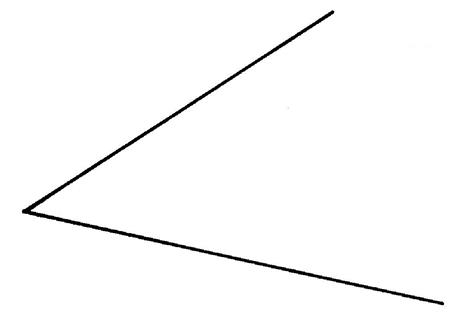
Activités …… 1°)Tracez l’axe se symétrie de l’angle ci contre en
utilisant le compas est la règle. Cette droite est le support de la bissectrice de cet angle.. |
|
|
|
|
Activités …… 1°)Tracez les deux axes de symétrie du segment. Ces deux droites
sont : le support du segment et la « médiatrice » du segment |
|
|
|
|
Les axes de symétrie du Rectangle : |
|
|
|
|
Activités …… 1°) Copiez l’image ci contre sur une feuille de
calque. 2°) Cherchez
par pliage les axes de symétrie. ; combien en trouvez
vous ?.....2….. Passez ces pliages en rouge, appelez les
« d » et « d’ » · « d » est la ………médiatrice …….de [ A B ] et [ DC] · « d’ » est la ……… médiatrice ……….de
[ A D ]
et [ BC] |
|
|
|
|
|
||
|
Tracez les sur la figure ci contre : |
|
||
|
A retenir : Tout
rectangle possède deux axes de symétrie qui sont les médiatrices des
côtés. |
|||
|
|
|
|
|
|
|
Les axes de symétrie du parallélogramme. |
|
|
|
|
Activités …… 1°) Copiez le parallélogramme ci contre sur une feuille de calque. 2°) Faites des
pliages afin de déterminer des
axes de symétrie. 3°) Que constatez vous ?
……………………………………….pour ce parallélogramme. |
|
|
|
Les axes de symétrie du triangle quelconque. |
|||
|
La figure ci contre représente un triangle
quelconque.( la reproduire sur un calque) Faites des pliages afin de déterminer des axes de
symétrie. Que constatez-vous ? ……………………………il ne possède pas d’axe de symétrie…………… |
|
||
|
|
Les axes de symétrie du triangle isocèle. ( info +++) |
|
|
|
|
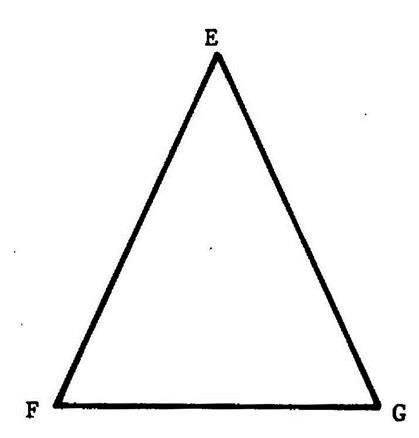
La figure ci contre « E G F »
représente un triangle isocèle .( la reproduire sur
un calque) [ FG ] est la base . [ EG ] et [ EF ] ont même longueur. Faites des pliages afin de déterminer des axes de
symétrie. Cherchez
par pliage des axes de symétrie. Combien en trouvez vous ?
…………un seul …… Passez en rouge cette droite . « F » et « G » sont …………………
par rapport à cette droite. Ce qui revient à dire que cette droite est la ……………………….de [ FG
] Tracez la sur le dessin ci contre
. ( Elle passe par le ………………..de [ FG ] ) |
|
|
|
A retenir : Tout triangle isocèle admet un
axe de symétrie qui est la ……………………….de sa base. |
|||
|
|
|||
|
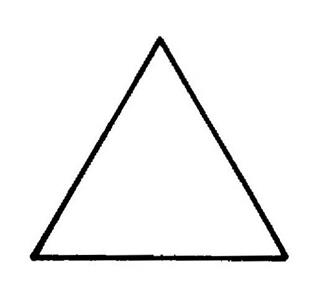
Les axes de symétrie du triangle équilatéral . (info ++++) |
|
||
|
|
|
||
|
Un triangle équilatéral est un triangle dont les
3 côtés ont la même ……Longueur……. Il peut être considéré comme triangle isocèle de
3 façons différentes. . Il y a donc ….trois……axes
de symétrie. Tracez les sur la figure ci-contre. |
|||
|
|
|||
|
|
Les axes de symétrie du trapèze isocèle. ( info ++++) |
|
|
|
|
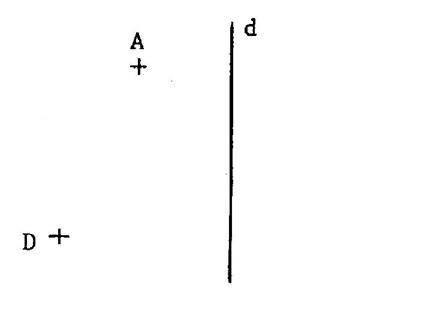
Ci – contre , voici une
droite « d » et deux points « A » et « D ». · Dessinez le point « B » symétrique de « A » par
rapport à « d ». · Dessinez le point « C» symétrique de « D » par rapport
à « d ». Vous pouvez dire que « d » est la
………..symétrique………..de [ AB ] et [ DC ] Tracez les côtés du quadrilatère
« ABCD » . Un tel quadrilatère s’appelle un trapèze isocèle. La droite « d » est …………………………….pour
« ABCD » [A D] a pour symétrique ……………..donc AD …. BC |
|
|
|
|
A retenir : Un trapèze isocèle est un trapèze qui a un axe de symétrie. Cet axe de
symétrie est la ……symétrique……………des bases. Dans un trapèze isocèle les côtés non parallèles
ont même ……..longueur……. |
|
|
|
|
|
|
|
|
|
Les axes de symétrie du losange . |
|
|
|
|
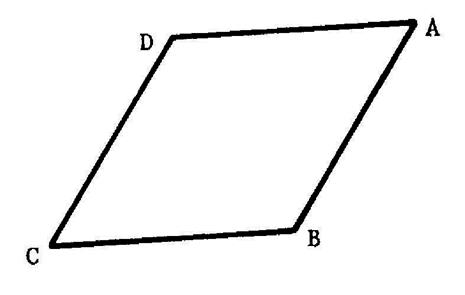
Ci contre on vous propose un losange. Ses quatre côtés
ont la même longueur : « AB = BC = CD=DA » Apparemment
, il y a deux axes de symétrie : Les droites ……………et ……………. ( tracez les sur
la figure ) Nous allons le prouver par un raisonnement : Puisque « AB= AD » alors
« A » est équidistant de « B » et de « D ». Puisque « CD= CB » alors
« C » est équidistant de « B » et de « D ». Donc la droite « (AC) » est ……diagonale……du
losange . Il en est de même pour (DB). Conséquence : ( AC ) et ( D B ) sont
perpendiculaires et [ AC ] et [ D B ] ont même milieu. |
|
|
|
|
A retenir : Tout losange admet « 2 » axes de
symétrie qui sont ses diagonales. Dans tout losange les diagonales sont ………perpendiculaires……….
Et se coupent en leur ……………..milieu…… |
|
|
|
|
|
|
|
|
|
Les axes de symétrie du carré. ( info ++ le
carré) |
|
|
|
|
Le carré est à la fois un rectangle et un
losange. Dessinez les axes de symétrie du carré ci contre. |
|
|
|
|
17/01/2013 |
|
|
TRAVAUX AUTO-FORMATIFS : remplir le document .. refaire les travaux
CONTROLE