1- Superposition de figures par pliage.

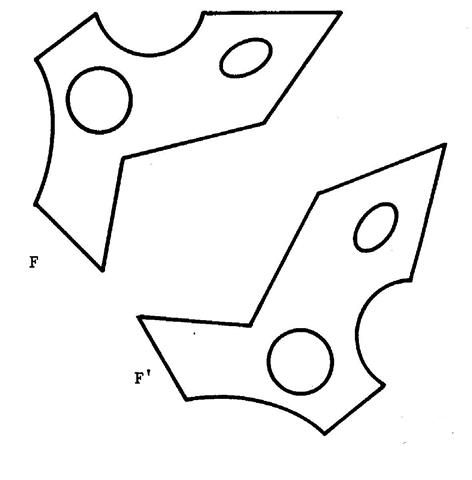
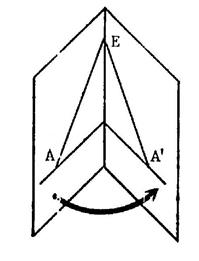
Activité 1 : prendre une feuille de calque et  reproduire l’image ci-dessous :

Lorsque que vous avez reproduit cette image, liez le morceau de calque de telle sorte que la figure « F’ »  s’applique sur la figure « F ».

Les deux figures coïncident -elles ?....oui ..

On dit que les deux figures sont superposables.

Vous  pouvez  constater que le pli est une droite.

Dépliez la feuille est repasser en rouge la droite de pliage.

Appelons « d » cette  droite.

Lorsque les figures sont bien à plat , c'est-à-dire « F » et « F’ » sont dans un même plan :

·       On dit alors : que « F » et  « F’ » sont symétriques par rapport à la droite « d ».  ( « d » est appelée : l’axe de symétrie ) ,

·       On dit aussi : que « F » et « F’ » se correspondent dans la symétrie orthogonale d’axe « d ».

·       On dit aussi que « F’ » est  la symétrique de « F » ( ou l’ image de « F ») dans la symétrie orthogonale d’axe « d ».

·       Qu’elle est alors dans cette symétrie , l’image de « F’ » ? ………………………

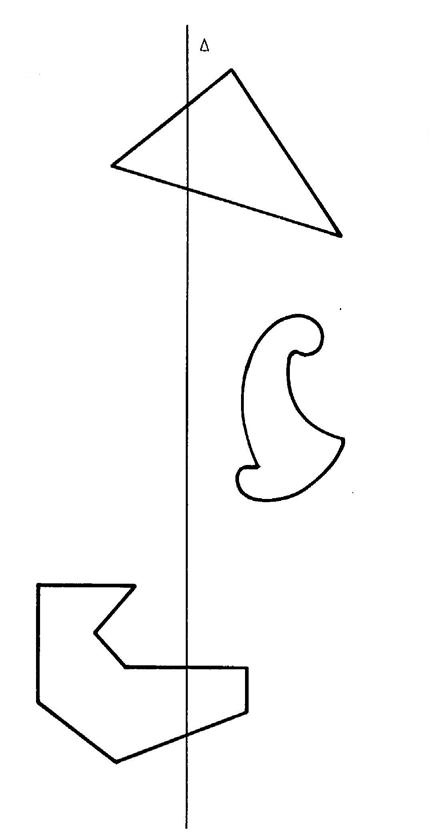
Activité 2 :

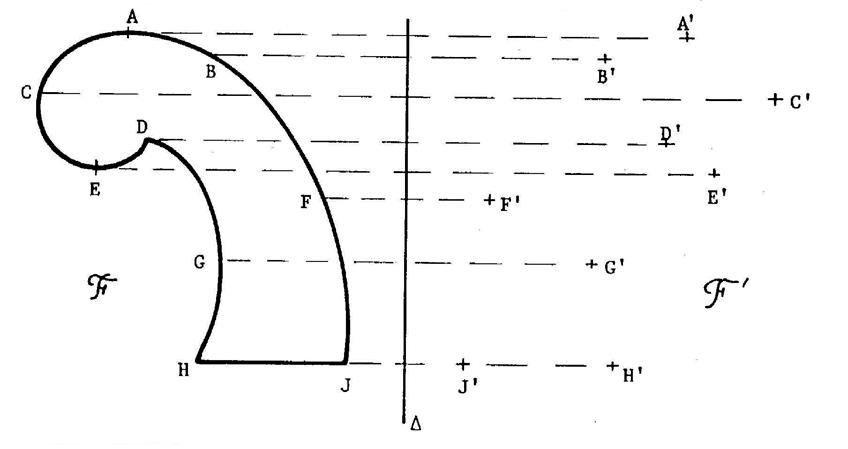
Prendre une feuille de calque  de la dimension du cadre ci contre.

Reproduire par transparence le dessin ci-contre.

Ensuite :

Pliez ce morceau de calque suivant la droite « delta » ( ) et dessinez par transparence les symétriques par rapport à ( ) des figures ci-contre.

Activité 3 :

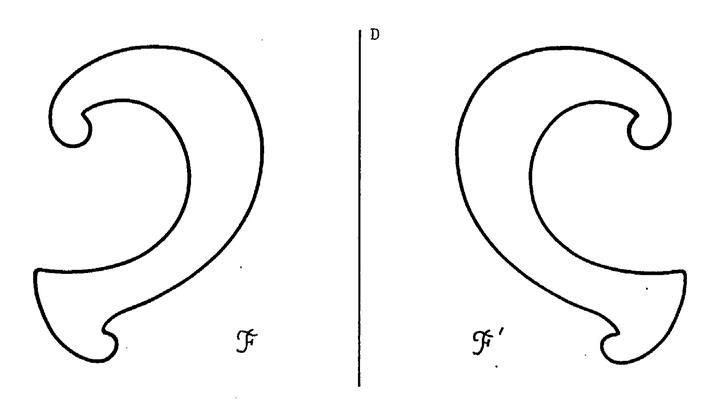
Observez ci – dessous , le dessin de deux figures symétriques par rapport à la droite « D ».

Vous pouvez imaginer que vous pliez la feuille suivant la droite « D ».

La figure « F’ » viendra en coïncidence avec la figure « F » .

Mais si ces figures , au lieu d’être dessinées sur une feuille de papier , sont dessinées sur de la pierre ou une plaque de métal ou etc.….vous concevez qu’il ne soit pas possible .Vous comprenez qu’il n’est pas possible de faire un pliage pour les superposer…

Il faut donc imaginer , trouver, un procédé mathématique qui permette de dire sans pliage dans quelles conditions deux figures sont symétriques par rapport à une droite .

2- Symétrie d’un point dans une symétrie orthogonale.

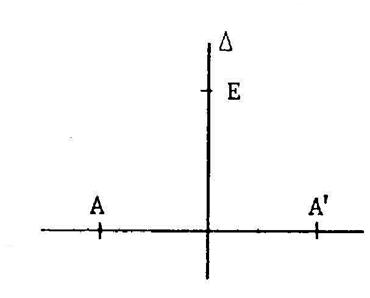
Un triangle  quelconque est dessiné sur une feuille  de calque . ( ci contre)

Pliez le calque suivant la droite ( ) ;
 Le point « A » vient coïncider avec un point « unique » du calque. Appelons « A’ » ce point.

Marquez le  point « A’ » sur le calque.

« A’ » est  le symétrique de « A » par rapport à ( ).

·       Considérons un point « E »  quelconque sur ( ).

·       Le segment [ EA ] coïncide avec les segment [ EA’ ]  donc  EA…= . EA’  quelque soit « E »  sur ( ).

Dépliez le caque et tracez le segment [ AA’ ]  .

Tout calque ressemble à la figure ci-contre.

Tout point  de  ( )   est ………à égale distance……. de « A » et « A’ », donc ( ) est la ……… symétrie………….de  [ AA’ ] 

De même par pliage, déterminez « B’ » le symétrique de « B » par rapport à  ( ) .

Tracez  [ BB ’ ] . Vous pouvez dire que  «  »   est  ………………………. de  [ BB ’ ].

·       Reprenez le calque. Quel est le symétrique du point « C » ? ………………………………… ;

·       Où sont situés les points qui sont leur propre symétrique ? ……………………………………….

A retenir :

Etant donné une droite «  »  , dans la symétrie orthogonale d’axe «  »  , le symétrique  d’un point « M » non situé sur «  »   est le point « M’ » tel que «  »   soit la  …………………………..de  [M M’ ].

Le symétrique d’un point « M » situé sur «  »  est ce point lui –même.

·       Construction du symétrique d’un point par rapport à une droite.

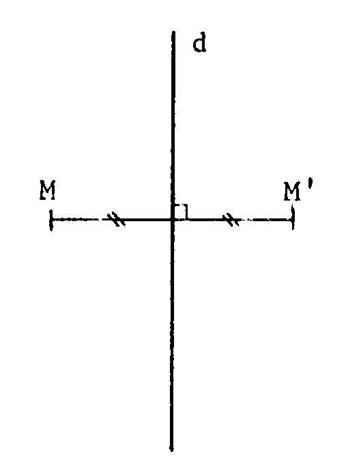
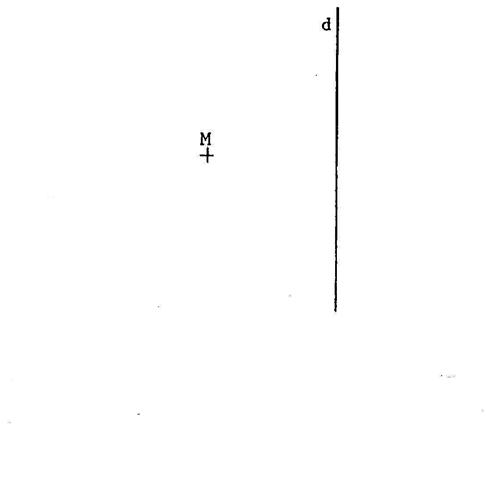
Ci contre une droite « d » et un point « M » ,non situé sur « d ».

Activité : On vous propose de construire sans pliage le symétrique de « M’ » de « M » par rapport à « d ».

(autrement dit : tracer l’image de « M »  sur une perpendiculaire  par rapport à « d » appelé : « M ’ ».

Or nous avons vu dans le cours sur la média……s. Que cela signifie :

·       « d » est la médiatrice du segment [M M’ ]  et

·       « d » passe par le milieu de  [M M’ ]

Activité suivante :

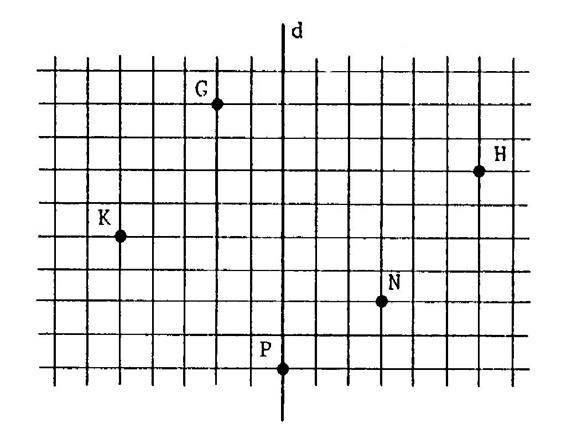
Construire les points « G’ » ; « H’ » ;  « K ‘ » ; « N’ » ; « P’ » symétrique par rapport à « d »  des  points : « G » ; « H » ;  « K » ; « N » ; « P »

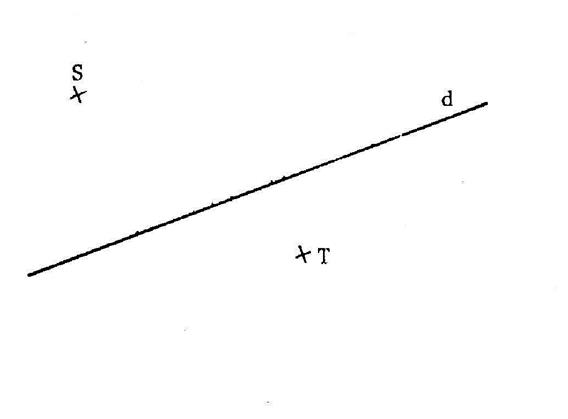
Construire avec une équerre ou un compas  les points « S’ » ; « T’ » symétrique par rapport à « d »  des  points : « S » ; « T » .

3- Image d’une figure dans une série orthogonale.

Ci contre on vous donne une droite « ( ) » et une figure « F ».

Sur la figure « F » on a placé des points . (qui peut être un ensemble points).

L’image de « F » dans la symétrie orthogonale par rapport à ( ) est la figure « F’ » constituée par l’ensemble des points qui sont symétriques des points de « F ».

Sur le dessin ci contre, on a choisi quelques points de « F » et on a déterminé leurs images. En imaginant que l’on fasse la même chose pour tous les points de « F », complétez la figure « F’ » .

·       Images de figures simples.   ( voir @ La symétrie orthogonale de figures géométriques simples)

D’après ce que l’on a vu dans les activités précédentes , on peut dire 

Dans toutes les  symétries orthogonales, toute figure et son image sont superposables.

Donc ,dans toute symétrie orthogonale une figure et son image ont même forme et même dimensions.

On peut donc déclarer : ( après avoir  vérifié)que :

·       L’image d’une droite est une droite.

·       L’ image d’un segment est un segment superposable.

·       L’image d’un angle est un angle superposable.

·       L’image d’un triangle est un triangle superposable.

·       L’image d’un cercle est un cercle de même diamètre.

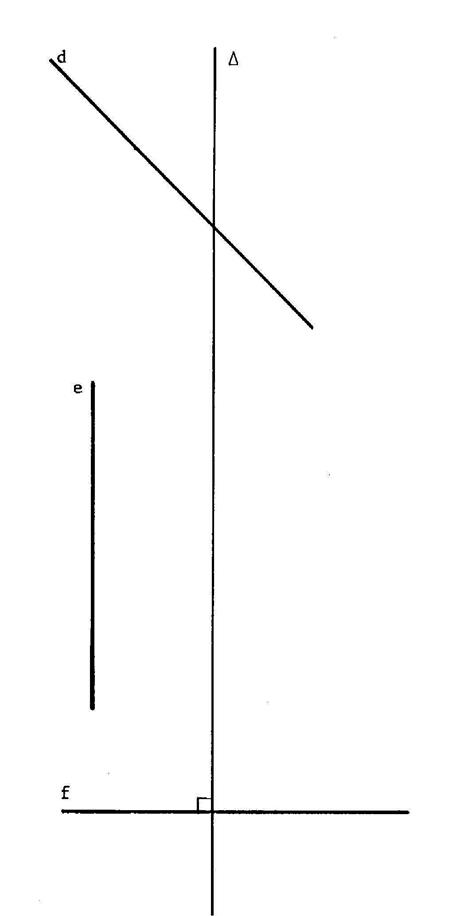
Les centres de ces cercles sont des  symétriques par rapport à l’axe de symétrie.

Activités….. :

Vous allez vérifier que l’image d’une droite est bien une droite :

·       Reproduire sur calque l’image ci contre :

·       Pliez la feuille autour de ( ) ,

·       Dessinez les images « d ’ » ; « e’ » ; et « f ’ » des droites « d » ; « e » et « f ».

·       Dépliez la feuille et constatez que :

1°)  « d’ » l’image de la droite  « d » est une symétrie orthogonale .

    Les droites « d » et d’ » se coupent en un point situé sur ( ).

2°) « e » est une droite parallèle à ( ).

     « e ‘ » l’image de « e » est une ………………………………….. ;

   Les droites ( ) , « e » et  « e’ » sont ……………… »parallèles ……………………… ;

3°) « f » est une droite perpendiculaire à ( )

  « f ’ » l’image de « f » est  ………………………………….avec « f » , c’est donc une …………… »perpendiculaires »…………………………….

Conséquence : Si des points sont alignés , leurs images sont des points … »alignés »………….

4°) Construction de l’image d’une figure.

Activité ….. :

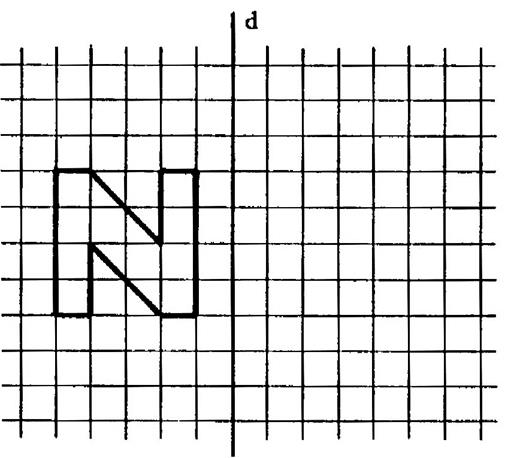
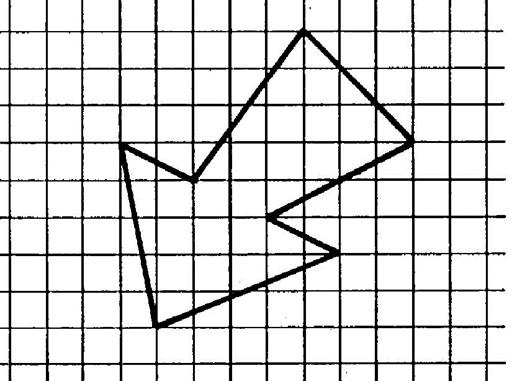
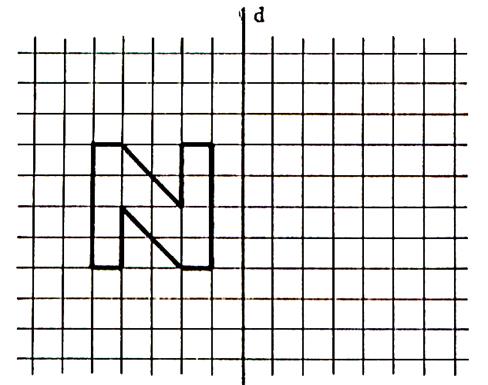
En utilisant le quadrillage, dans chacun des deux cas, dessinez l’image ci contre dans la symétrie orthogonale d’axe « d ».

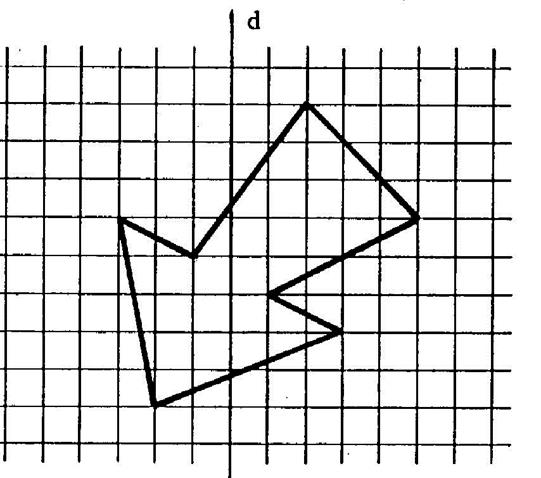
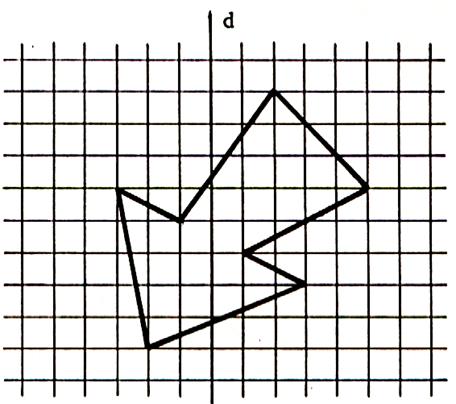
En utilisant le quadrillage, dans chacun des deux cas, dessinez l’image ci contre dans la symétrie orthogonale d’axe « d ».

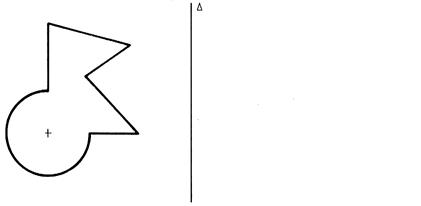
Tracez sur la figure ci contre un axe  ( ) »  horizontal,  séparant la figure en deux parties . En utilisant le quadrillage, dessinez l’image ci contre dans la symétrie orthogonale d’axe ( ) ».

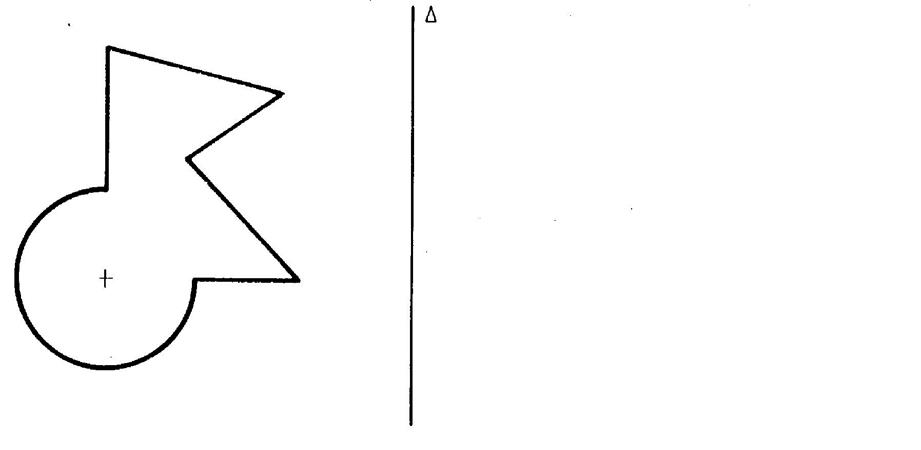
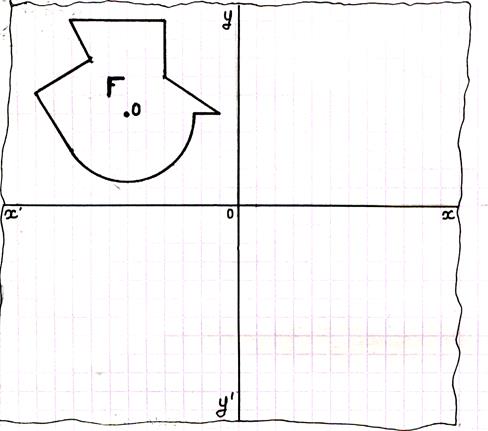
On vous demande de dessiner l’image ci-dessous dans la symétrie orthogonale d’axe ( ) ».

Pour cela :

·       Nommer les points « particuliers » : intersection de segments ; centre du cercle ;….autres pour utiliser comme éléments de vérification..

·       Tracer les droites perpendiculaires à « ( ) », comme vous l’avez appris précédemment. ( en traits fins..)

·       Vous allez déterminer l’image  de ces points.

·       Vous joignez ces points.  ( vérifiez vos tracés avec quelques points pris au hasard )

5°)  Autre façon de construire le symétrique d’un point :

Activité …n°…. :

Ci contre on vous donne une droite « d » et un point « M » non situé sur « d ». ( en dehors de « d »)

1°) Choisissez un point « R » quelconque sur « d ».

2°) Tracer un arc de cercle de centre « R »  passant  par « M ».

3°) Choisissez un point  « T » quelconque dur « d ».

4°) Tracer un arc de cercle de centre « T »  passant  par « M ».

5°)  Nommez « N »  le point d’intersection des deux arcs de cercles .

Conclusion :

« R » étant centre d’un cercle passant par « M », alors « R » est équidistant de « M » et de « N » .

De même « T » est équidistant de « M » et de « N » .

Donc : « R » et « T » sont situés sur la médiatrice de [M N].

Donc la droite « d » est « médiatrice de  [M N].

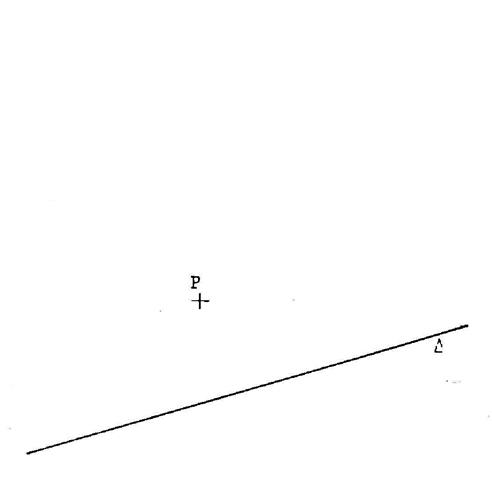
Activité …n°…. :

Ci contre on vous donne une droite « ( ) » et un point « P » non situé sur « ( ) ». ( en dehors de « ( ) »)

Tracez  le symétrique  « S » de  «P » par rapport  à   « ( ) »

Tracer la symétrie orthogonale

- d’un segment de droite.

-d’une droite.

- d’un angle

Tracer la symétrie orthogonale d’une figure géométrique simple.

Cercle

Disque

triangle

Carré

Rectangle