« MEDIATRICE »

1°) Médiatrices d’un segment.

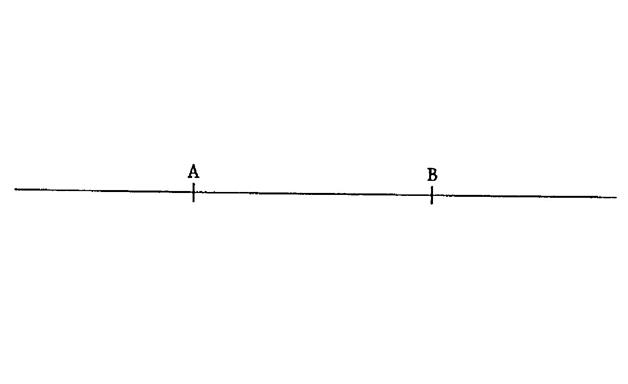
Activité  découverte :  ( à faire sur la figure ci-dessous )  :On vous donne deux points « A » et « B »

·       Tracez deux cercles ayant pour  centres respectifs « A » et « B » de même rayon : 19 mm.

(constat : ces deux cercles ne se coupent pas ; ils n’ont pas de point commun)

·       Maintenant, tracez deux cercles ayant pour centres respectifs « A » et « B »  de même rayon : 26 mm.

(constat : ces deux cercles  se coupent   en deux points. Marquez au bleu  ces deux points )

·       Vous allez augmenter le rayon de 5 mm, et  vous tracez les deux cercles de centres respectifs « A » et « B ».

(constat : ces deux cercles  se coupent   en deux points. Marquez les au bleu  )

·       Puis recommencez en augmentant chaque fois les rayons de « 5 mm » , jusqu’à environ 50 mm.

(le constat est toujours le même : ces deux cercles  se coupent   en deux points. Marquez les tous au bleu  )

·       On peut alors constater , en prenant une règle , que ces points bleus sont « alignés » ; tracez alors cette droite  passant par tous ces points. Nous l’appellerons « médiatrice » ( droite « d »)

·       Activité 1 :

Considérons un point bleu quelconque. Etant situé à l’intersection de deux cercles de même rayon, de centre respectifs  « A » et « B », on peut dire que ce point bleu est à la même distance de « A3 et de « B » . On dit que ce point est « équidistant » de « A » et de « B ». 

Et tout point équidistant de « A » et « B » peut-être obtenu en utilisant ce procédé.  ( compas )

• Activité 2 :

Choisissez un rayon quelconque ( distance entre les deux pointes du compas  non imposé) et déterminez ,sur le dessin ci-dessus, d’autres points équidistants de « A » et de « B ».

Que constatez vous ? : je constate que ces points sont situés sur la droite…

On peut conclure que  tout  point  équidistant de « A » et « B » est situé ………..sur une droite.

• Activité 3 :

Choisissez un point « M » quelconque de la droite (autre qu’un point bleu)

Tracez le cercle de centre « A » passant par « M »  et   le cercle « B » passant par « M ».

Vous remarquez que ces deux cercles ont le même ………………Rayon….

Il en serait de même pour n’importe quel point de la droite « d »

On peut dire alors que tout point de la droite « d » est « équidistant » de « A » et « B »

La droite « d » est appelée « médiatrice de  [ AB ]   (segment « AB »)

A retenir :

La médiatrice d’un segment  est une droite .  La médiatrice est l’ensemble des points équidistants des extrémités de ce segment.

2°) Propriété de la médiatrice d’un segment.

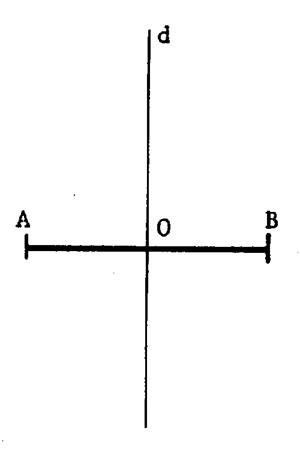
Reprenons la figure du chapitre ci-dessus  et considérons les droites « d » et « (AB) ».

Que pouvez vous dire de la position relative de ces droites ?   ( utilisez une équerre )  . (info @) .

Réponse : les deux droites sont perpendiculaires.

• Activité 4  :

Appelons « O » le point d’intersection de « d »  avec «  ( A B ) »

« O » étant situé sur « d », il est équidistant de   «  A »   et  « B »  et comme il est situé que le segment [ AB ]   (segment « AB ») on peut dire alors que « O » est équidistant des extrémités du [ AB ]   (segment « AB ») .

En conclusion , on peut dire que : la médiatrice d’un segment coupe ce segment en son milieu et est perpendiculaire au support de ce segment.

Question : Existe-il une autre droite passant par le milieu d’un segment et perpendiculaire au support de ce segment ?....(réponse : non ) .

A retenir :

La médiatrice d’un segment est la droite passant par le milieu de ce segment et perpendiculaire au support de ce segment .

On a donc deux façons d’exprimer qu’une droite est médiatrice d’un segment.

3°) Construction  de la médiatrice d’un segment.

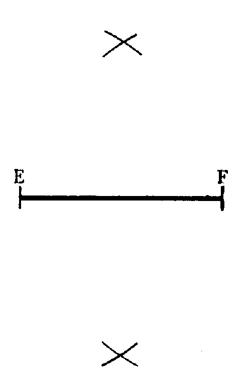
On se propose de construire la médiatrice du segment  [ E F ].

Pour cela on a deux méthodes possibles :

Méthode 1 @ : Avec une règle on effectue la mesure de E à F , on divise la mesure par deux ; puis on place le milieu de EF .Puis on trace avec une équerre  la droite passant par le milieu et perpendiculaire au support du segment.

Méthode 2 : On procède comme décrit au chapitre « 1 », mais au lieu de tracer plusieurs cercles , on se contente de tracer une paire de cercles sécants (qui se coupent deux à deux), remarquez que l’on ne trace que des arcs de cercle. !

Ces arcs se coupent deux à deux  en deux points  , la droite passant par ces deux points est alors la médiatrice de  [ E F ] . Tracez cette droite !

Remarque 1 :

Des 2 méthodes , la méthode n°2 est la plus précise , c’est celle que l’on utilise couramment.

Remarque 2 :

Lorsque l’on emploie le mot « construire » , cela signifie :   Utiliser , pour  tracé ,   la règle non –graduée et le compas (uniquement )

Activité 5 : 

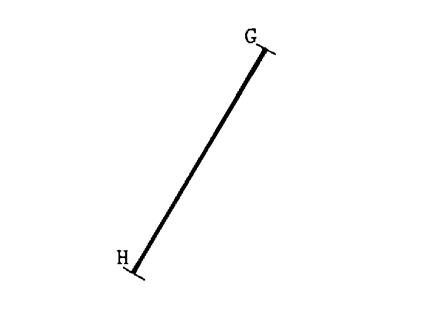
Construisez ( en utilisant la deuxième méthode) la médiatrice du segment  [ G H ] ci – contre .

Remarque 3 :

On a vu que la médiatrice d’un segment coupe ce segment en son « milieu » . ON peut alors utiliser alors la construction précédente pour déterminer le milieu d’un segment.,

Activité 6 :

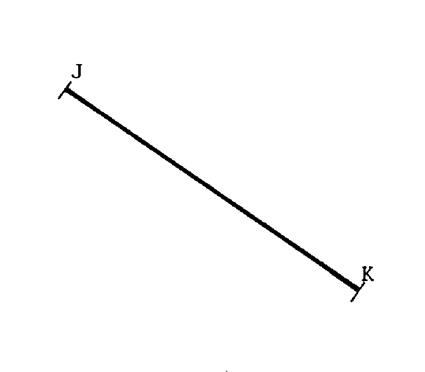
Construisez le milieu « I » du segment  [  J K ]  ci contre.

4°) Médiatrices des côtés d’un triangle.

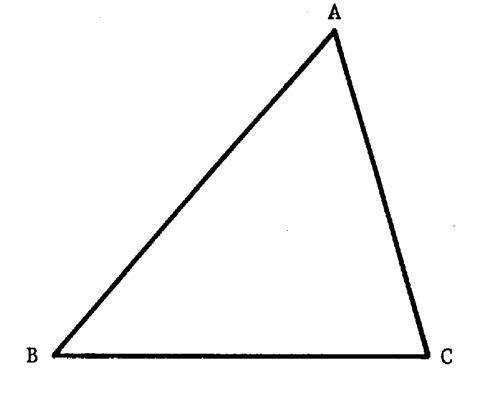
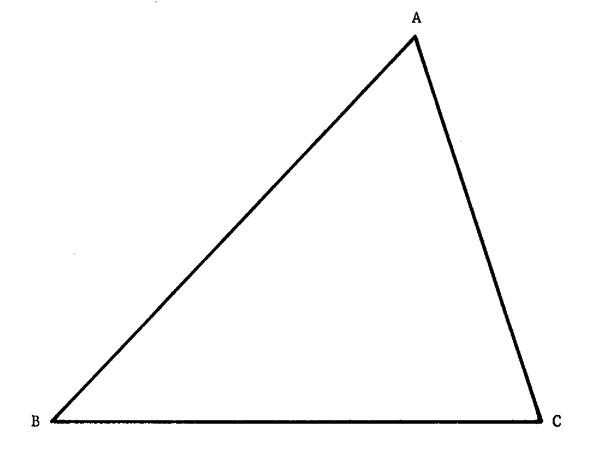
Ci contre on vous donne un triangle « ABC ». Il a trois côtés.

Ces côtés sont les segments :

……[  A C  ] ……[  C B  ]……. [  B A  ]..

Activité 1 : Tracez les médiatrices de ces segments.

Ces trois droites se coupent en un même point. Appelons « O » ce point.

Activité 2 : Comparez  les distances du point « O » aux trois points « A », »B » et « C ».

Que constatez-vous ?

Activité 3 : Vous pouvez alors tracer le cercle de centre « O » passant par « A »,  « B » et « C ».

( info + :voir médiatrice et le cercle circonscrit )

II ) MEDIANES   d’un triangle.

Il y a 3 médiane dans un triangle !

Une médiane d’un triangle est un segment limité par un sommet et le milieu du côté opposé.

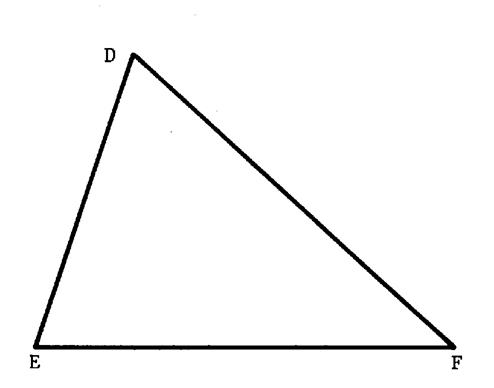
Remarque : la « médiane » désigne aussi la droite qui est le support de ce segment.

Activité 4 : Tracez les médianes du triangle « DFE ».

Vous appellerez : « D ’ »  le milieu de  [  E F ] ; « F ‘ »le milieu de  «  [  D E ] et « E ‘ » le milieu de  [  D F  ]

Info.

Ces trois droites se coupent en un même point . Nous appelons ce point « G ».

On vous demande de comparer les longueurs des segments :

Comparaison : ( faire une division )

 D G =  ………………………mm…

G D ’ =………………………mm…………

D G = ……G D’

E G = …………………………mm…….

G E ‘ = ………………………mm………

E G = …….G E ‘

F G  = …………………………mm……

G  F ‘ = …………………………mm.

F G = …….G F ‘

Info ++

III ) Perpendiculaire à une droite en un   de ses points.

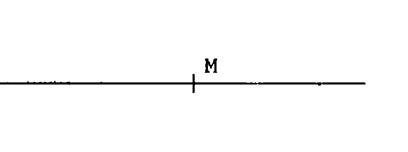
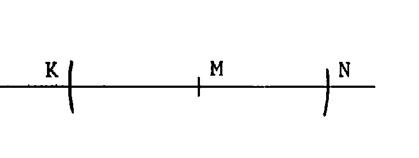
Activité 5 :

Les points « M », « N », « K »  appartiennent à la droite « d » .( notée « d » sur le dessin ci contre).

Ci contre , on vous donne une droite « d » et « M » un de ses points. On vous propose de construire ( avec la règle et le compas) (donc sans l’équerre)  la perpendiculaire à « d » passant par « M » .

Procédure : On prend « M » comme centre ( La pointe du compas en « M »,  On trace deux arcs d’un même cercle qui coupe la droite « d » en deux points « K » et « N » .

Observation : « M » est alors le milieu de  [ K N ]

Il ne vous  reste plus qu’à tracer la médiatrice de [ K N ] ( comme on l’a fait au chapitre «3°) » , la  deuxième méthode.

Complétez la phrase : Cette droite passe   par « M » et est « perpendiculaire » à « d ».

Info ++

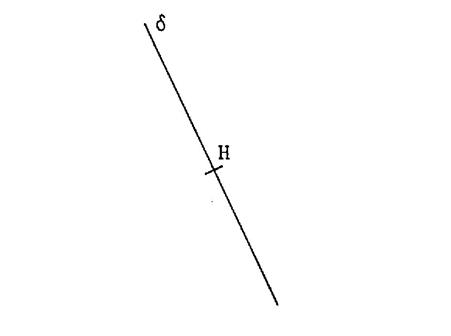
Activité 6 : 

On vous demande de construire la perpendiculaire en « H » à la droite « d »

IV ) Perpendiculaire « abaissée »  d’un  point sur une droite.

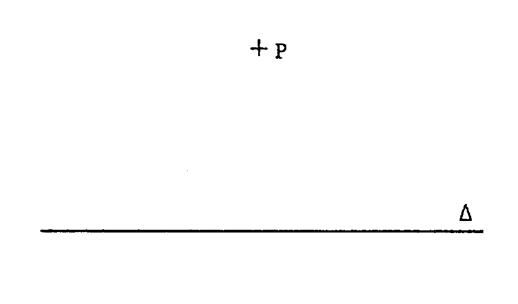
Etant donné un point « P » et une droite «  » , tu vas construire la perpendiculaire à «  »  à « P » .

De « P » comme centre, trace un arc de cercle qui coupe «  » en « A » et « B » .

Il est donc situé sur la médiatrice de [ A B ].

Puisque cette médiatrice est perpendiculaire à ( A B ) , alors la droite cherchée est cette médiatrice.

Activité 7 : A vous de tracer cette médiatrice ( ci contre) .’voir l’activité 5.

Activité 8 :

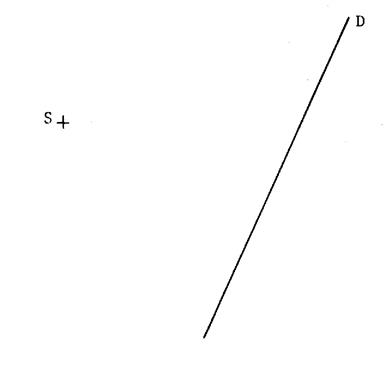
On vous demande de construire la perpendiculaire à la droite « d » passant par le point « S ».

Info ++

V ) Hauteur d’un triangle.

Un triangle possède 3 hauteurs . Une hauteur d’un triangle est une droite passant par un sommet et perpendiculaire au côté opposé à ce sommet.

Remarque : « hauteur » désigne aussi le segment porté par cette droite et limité par le sommet et le côté opposé.

Activité 9 : .On vous demande de construire les hauteurs du triangle « ACB » ( faîtes la construction en vous aidant de l’activité 8.).

Ces trois droites se coupent en un même point.. ( appelé : orthocentre »)

Fin le 29 – 12- 2012