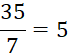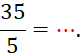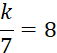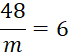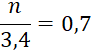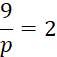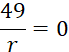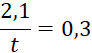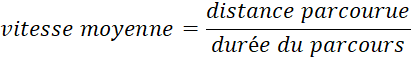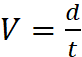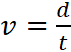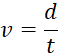Fiche :

1°) Quotients de nombres entiers naturels.

2°) Quotient de nombres décimaux

3°) Quotient entier approché d’entiers naturels.

4°) Quotient décimal approché d’entiers naturels ou de décimaux.

5°) Les égalités ayant la même signification que le produit :  «  a = b  c »

6°) Quotient d’un produit par un nombre.

7°) Quotient d’un nombre par un produit.

COURS.

1°) Quotients d’entiers naturels.

Activité 1 :

·       Effectuez les divisions ci-dessous ( maximum 3 chiffres après la virgule).

·       Faîtes la vérification ( posez les opérations sur la feuille)

Opération n°  1

Opération n°  2

Opération n°  3

2

2

1

13

4

2

6

,

8

5

9

,

18

·       Cas de l’opération N°1 :

Le reste est ….. …..

« 17 » est le quotient entier exact de « 221 » par « 13 » :     On écrit   221 13   =   …………   ou     =   …..  , cela signifie que 221 = …  ….

Remarque :

Pour exprimer  « 221 = ….  … »  on peut utiliser le vocabulaire suivant : ( ce vocabulaire qui ne s’utilise uniquement dans le cas de nombres entiers ) 

« 221 » est un … … de « 13 »  ( ou de « 17 »)  ou « 221 »  est  … …….par  « 13 »  ( ou « 17 »)    ou   « 13 »  ( ou « 17 »)    est un ………. de « 221 » ou  « 13 »  ( ou « 17 »)    ………….. « 221 »….

·       Cas de l’opération n°2 : ( parvenu  à deux chiffres après la virgule on s’aperçois que le reste est « nul »)

Le reste est …………….

On dit que « … »  est le quotient décimal exact de « 426 par 8 »

On écrit :  426   8 = …………….    ou       =  ………..   signifie que  426 =  ….   ……………

·       Cas de l’opération n°3 :

On constate que la division ……………………………………………………………………………………..

A partir d’un certain moment, les restes successifs sont toujours égaux à ……………..

Donc , après « 3,27 » les chiffres successifs du quotient seront toujours des « …… » 

On est donc certain que la division ne se termine pas.

On dira alors que : Le quotient n’est pas un « décimal » car il y a une infinité de chiffres après la virgule.

Le quotient de « 59 par 18 » est alors le nombre qui s’écrit  :       .   et    59  18  =  

Qui plus est  l’égalité  : 59  18  =      signifie que    «  59 =  18  »

En définitive :

Dans la division d’un entier par un autre entier,

-        Si la division se termine ( par 0) , le quotient est un nombre entier ou un nombre décimal.

-        Si elle ne se termine pas , le quotient est un nombre « non décimal ».

Il n’y a que dans le cas où le diviseur est « zéro » que le quotient n’existe pas.

A retenir :

On désigne par :   « a » et « b » sont des nombres entiers naturels ( b  0 ) ,

Le résultat de la division : Le quotient de « a » par « b » existe toujours, il s’écrit   «  a b »     ou  «  » .

Alors trois cas concernant la nature du quotient : Il peut être entier, décimal ou non-décimal. 

Le quotient « q » est le nombre par lequel il faut multiplier « b » pour obtenir « a »

« a  b = q »   signifie « a = b q »

«  »  signifie « a = b  q »

Remarque :

Nous vous avons parlé de quotient « exact »  ou de quotient décimal « exact » , le mot « exact » peut paraître superflu car le quotient est nécessairement exact, mais on utilise le mot « exact »  en opposition à « approché » car on parle aussi de « quotient approché » pour désigner la « valeur approchée du quotient »  ( voir le chapitre « 3 »)

(info ++ : expression d’un résultat)

2°) Quotient de nombres décimaux.   ( on dit aussi : quotient de décimaux)

(conseil : n’utilisez pas la calculatrice…)

Opération n°  4

Opération n°  5

Opération n° 6

23

,37

0,41

0 ,

0  5

18

0,14

1

5,

4

8

2,7

·       Cas de l’opération N°4 :

Le reste est …..…..

« 57» est le « quotient entier exact » de « 23,37 » par « 0,41 » :     On écrit   23,37 0,41   =   …………   ou     =   …..  , cela signifie que 23,37 = ……  ……….

·       Cas de l’opération N°5 :

- Le reste est ….. …..

- On dit que « ……..» est le « quotient décimal exact » de  « 0,0518 » par « 0,14 » .

- On écrit « 0,0518  0,14  = ……… »  ou «  »

-   «  »  signifie que :  «  0,0518 = ………….. »

·       Cas de l’opération n°6 :

Que constatez-vous ? On constate que la division ……………………………………………………………...

A partir d’un certain moment, les restes successifs sont toujours égaux à ……………..

Donc , après « 5,73 » les chiffres successifs du quotient seront toujours des « …… » ….

On est donc certain que la division ne se termine pas.

On dira alors que : Le quotient n’est pas un « décimal » car il y a une infinité de chiffres après la virgule.

Par analogie avec les nombres entiers : 15,48  2,7  s’écrit aussi

Le quotient de « 15,48  par 2,7 » est alors le nombre qui s’écrit  :       ce nombre peut s’écrire aussi       ( ici rappel)

Qui plus est  l’égalité  : 59  18  =      signifie que    «  59 =  18  »

15,48  2,7  =      signifie      15,48  = 2,7   

·       De l’étude de ces trois exemples il en ressort que :

A retenir :

On désigne par :   « a » et « b » sont des nombres décimaux  ( b  0 ) ,

Le résultat de la division : Le quotient de « a » par « b » existe toujours, il s’écrit   «  a b »     ou  «  » .

Alors trois cas concernant la nature du quotient : Il peut être entier, décimal ou non-décimal. 

Le quotient « q » est le nombre par lequel il faut multiplier « b » pour obtenir « a »

« a  b = q »   signifie « a = b q »

«  »  signifie « a = b  q »

Activités 1:

Sachant que « 3425  25 = 137 »   , sans faire d’autres calculs complétez :

 342500  0,25

=   

3425000   2500

=

34,25     2,50

=

0,3425     250

=    

0,003425     0,000025

=

0,03425     0,0250

=

3425  25000

=    

3,425    0,000 25

=

342,5    0,00 250

=

3°) Quotient entier approché d’entiers naturels.

Effectuez la division ci-contre afin d’obtenir un quotient entier.

Faîtes la vérification.

(Posez les opérations , mais n’oubliez pas le reste …….)

Ecrire l’égalité correspondante :  «  2457  =  53   ……...+ ….… »

2

4

5

7

5

3

3

3

7

4

6

1

9

Remarque :

On n’a pas le droit d’écrire que : 2457  53  = 46   ou que   , car le reste n’est pas égal à « ……… ».

Toutefois , on peut écrire  que :  2457   53   46   ou   

(  le symbole  se lit « est voisin de » )

« 46 » est appelé le « quotient approché » ( par défaut) de « 2457 par 53 ».

« 46 »  est aussi appelé la partie entière du quotient  de   .

Situation problème n°1 :

On veut ranger  187  C.D   dans des coffrets.

Sachant que chaque coffret à une contenance de   12  C.D. 

Combien de coffrets faudra-t-il ?

Situation problème n°2 : (info +le système sexagésimal +)

On vous demande d’exprimer « 15 853 s » en heurs ( h) , minute ( min) et seconde ( s)  .

Sachant que dans une minute on compte « 60s » :    1 min = 60 s.

On vous demande de déterminer le nombre de minutes qu’il y a dans « 15 853 s » 

. soit :  264 min 13 s

Sachant que dans une heure on compte « 60 min » :    1 h = 60 min.

Déterminez le nombre d’heures contenues dans « 264 min ». Calcul :   264   60 =  ……. h  +  …… min   soit  … h ….. min

En définitive : 15 853 s  =  …… h …….. min ……… s

1

5

8

5

3

60

3

8

5

264

2

5

3

1

3

2

6

4

6

0

2

4

4

Situation problème n°3 :

Exprimez de même :  «  374 813 s »  =  jour (d) ……heure (h) ……………minute (.min) …………….seconde (s).

4°) Quotient décimal approché d’entiers naturels ou de décimaux.   ( info +++ : arrondir à « tant prés »)

Que les nombres soient entiers ou décimaux, il se peut que la division ne se termine pas.

Ci -contre on vous présente une division : « 724,637  par 83,17 »  avec trois chiffres après la virgule.

Vérification :

   ( 83,17 ……...) + …………….……

= ………………..…….+ ……………..….

= ……………………………….

7

2

4 ,

6

3

7

83,17

5

9

2

7

7

8,712

1

0

5

8

0

2

2

6

3

0

0

0

5

9

9

6

« 8 » est le quotient approché à

« 1 »  près par défaut   de « 724,637  par 83,17 » 

« 9 » est le quotient approché à

« 1 »  près par excès   de « 724,637  par 83,17 »   

« 8,7 » est le quotient approché à

« 0,1 »  près par défaut   de « 724,637  par 83,17 » 

« 8,71 » est le quotient approché à

« 0,01 »  près par ……………..   de « 724,637  par 83,17 » 

« 8 ,713» est le quotient approché à

« …………… »  près par ……………   de « 724,637  par 83,17 » 

5°) Les égalités ayant la même signification que le produit :  «  a = b  c »  (info ++ « algèbre »)

« a », « b » « c » représentant  des décimaux non nuls quelconques, on a vu  que «   » signifie que « a = b c »

De même : «   » signifie que « a = c b » ; or    « b c »= « c b »  donc :

«   » ; « a = b c » ; «   »   sont trois égalités qui ont la même signification.

Exemple : 

35 = ……..  …

Ces trois égalités qui ont la même signification.

Activité :      Complétez le diagramme ci-dessous

« a = b c »

Signifie

Signifie

Signifie

Activités  N°…:Dans chacune des lignes ci-dessous, les égalités ont la même signification.

Complétez ces égalités en commençant par celle qui vous paraît la plus facile .

= ….. 8

Signifie que

72 = .9.…8.

Signifie que

  =  ……

   = …..

Signifie que

……. =  6  0,5

Signifie que

  =  ……

  = …..

Signifie que

1 = 2,5 ….

Signifie que

  =  ……

  = …..

Signifie que

…….= …...….

Signifie que

  =  0,3

Activités  N°…:    Dans les égalités ci-dessous , déterminez ( si cela est possible) la valeur des nombres représentés par les lettres.

7   d   =   42

e   5  =   9

f   0   =   53

3   g   =   8

0,4   h   =   24

i   19  =   0

1,3    j   =   9,1

Application :

Situation problème : aire du rectangle.

Considérons un rectangle quelconque. (voir ci-contre)

Appelons « L » sa longueur , « l  »  sa largeur , « A » son aire .  on écrit : A =  L    .

Complétez le diagramme.

« A = L   »

Signifie

Signifie

Signifie

Calcul 1 :

La longueur d’un rectangle est de  « 0,9 cm » , sa largeur est de « 0,6 cm » , son aire est de : …………………….

Calcul 2 :

L’aire d’un rectangle est de « 1,3 m² » , sa longueur est de  « 5 m »  , sa largeur est de : ……………………

Calcul 3 :

L’aire d’un rectangle est de « 264  mm² » , sa largeur  est de  « 11 mm »  , sa longueur  est de : ……………………

6°) Quotient d’un produit par un nombre.

On vous donne trois rectangles de largeur ( ) de longueur « L » et d’aire « A ».

Retangle 1 :

On vous demande de partager chaque largeur en trois segments de même longueur.

Vous déterminez ainsi « 3 » rectangle de longueur « L » et de largeur :  ( 3) .

Passez en couleur un de ces rectangles.

Rectangle 2

On vous demande de partager chaque longueur  en trois segments de même longueur.

Vous déterminez ainsi « 3 » rectangle de longueur « L 3 » et de largeur :  ( ) .

Passez en couleur un de ces rectangles.

L’aire du rectangle coloré est égal à :  L  ( 3)

L’aire du rectangle coloré est égal à : ( L3)   ()

Vous constatez que dans les deux cas  l’aire du rectangle est le  « ………… » de l’are « A »  c'est-à-dire  «  ( L    )  3 »

On peut écrire :

«  ( L    )  ….. »  =

«  L   (    3 ) »  =

« ( …….. …… )     »

Activités …..n°……

( 20  15    30 ) 5  =

( ………… ) 5  =

= ……

=

( 20  15    30 )

( 20  15    30 ) =

……    …..    ….    =

=    …………..

( 20  15    30 ) 5  =

=

20 ( 15    30 )

20 ( 15    30 ) =

……..   …..    ……   =

=    ……………..

=

20 15   ( 30  

20 15   ( 30  ) =

…….    ……    ……    =

=    ……………

Il en serait de même en divisant (le rectangle) par  « 11 » par « 1,7 » par « 9,2 »…… on peut donc dire :

A retenir :

« Diviser un produit de facteurs par un nombre  revient à diviser l’un des facteurs par ce nombre »…

( a  b    c )  n  =

=

( 20  15    30 )

=

20 ( 15    30 )

=

20 15   ( 30

ATTENTION !!!

Rectangle 3.

·       On vous demande de partager chaque côté en « 3 » segments de même longeur.

Vous déterminez ainsi : « 9 » rectangles de largeur ( 3)  et de longueur ( L3)  .

·       Passez en couleur un de ces rectangles.

L’aire du rectangle coloriée  est égale à « A » divisé par « 9 »  , c'est-à-dire «  ( L    )  ……. »  =

On peut écrire que ( 3)  ( L3)  = ( L    )  …….. »

Vous constatez alors que dans le produit de deux facteurs, si on divise chaque facteur par un nombre (ici : 3 ), alors le produit est divisé par le produit de ces   nombres (ici 3 fois 3).

7°) Quotient d’un nombre par un produit.

(on sait que « 6 » divisé par « 2 »  est égal à  « 3 » et que   « 60 » divisé par « 20 » = « 3 »). Et que « 20= 4 fois 5 ».

Complétez : 60  ( 5  4 ) =  ….  …….  = ……

 et complétez : « ( 60  5 ) 4 =  …  ..… .. = ……     ;  ( 60  4 ) 5 =   ..… .. = ……   

Vous pouvez choisir d’autres nombres , vous ferez toujours la même constatation…..

A retenir :

Diviser un nombre par un produit de deux facteurs revient au même que de diviser le nombre par l’un des facteurs puis diviser le résultat par l’autre facteur.

« a  ( b  c) »  = «( a   b ) c) » = «( a   c ) b) 

Remarque : cette propriété peut se généraliser au cas de plus de deux facteurs .

Application : pour diviser un nombre par « 4 » , vous pouvez le diviser par « ………. » puis le résultat par « …….. »  .

Expliquez de même comment on peut diviser un nombre par « 6 »  ou par « 8 »……

8° )  Vitesse moyenne :

Info +++

Situation problème n°1 :

Pour parcourir une de 292 km en automobile, vous avez mis 4 h.

Si la voiture avait roulé régulièrement (c’est –à-dire à vitesse uniforme, dit aussi :à vitesse constante ) en 1 heure ( 1 h) elle aurait parcouru : 292 km  4  , c'est-à-dire « 73 km ».

On dit alors que sa vitesse moyenne est de 73 km par heure et on écrit : « 72 km/ h »   ou «  72 km. h^-1 ».

A retenir :

La « vitesse moyenne » est égale à la « distance parcourue » divisée par la « durée du parcours ».

D’où la formule :

Avec

« d = distance parcourue.

« t » = temps mis pour …….

Les unités : (couramment utilisées).

La vitesse peut s’exprimer :

en  « km/h »

Lire : kilomètres par heure.

en «  m / s »

Lire : mètre par seconde.

en « k m / min »

Lire : kilomètre par minute.

En …..etc.

Situation problème n°2 :

Un train  a parcouru « 63 » km en 42 min .

Question :  Quelle est sa vitesse moyenne en « km/min ».

Indication : vous pouvez commencer par calculer la vitesse en « km/ min »

Situation problème n°3 :

Un cycliste a parcouru « 178,4 km »  en « 5 h 33 min 20 s ».

Question : quelle est sa vitesse moyenne en km/h ?

Calcul d’une distance ou d’une durée.

Sachant que    , complétez le diagramme ci-dessous ( voir ci-dessus)

« v »  = vitesse moyenne

« d » = distance parcourue

d  =   …………

« t » = temps ( durée)

Signifie

Signifie

Signifie

Situation problème n°4 :

La vitesse du son dans l’air est d’environ   300 m / s.     ( lire : « 330 » mètres en « 1 » seconde).

Lors d’un orage , un pécheur (au bord de l’eau)  compte « 5 s » entre l’éclair et le bruit du tonnerre.

Question 1 :

A quelle distance l’observateur se trouve-t-il du lieu de l’impact de la foudre (d’autre dirait :  de l’orage ) ?

La fois suivante la foudre tombe, le pécheur compte  « 3 s »

Question 2 :

 A quelle distance sépare le pécheur de l’orage ?

Question 3 :

Que doit-il en conclure concernant sa sécurité  ? 

Situation problème n°5:

Un bon marcheur se déplace à la vitesse moyenne de 6 km / h.

Quel temps lui faut-il pour parcourir 9 km ?

9 / 6 = 1,5 h       ou 1 h 30 min.  (info : le système sexagésimal et système décimal)

Activité n°6 :  complétez le tableau ( faites  attention aux unités proposées)

Temps

5 h

15 min

………..s

Distance

170 km

….…..km

2 km

Vitesse moyenne

………….km/h

80 km / h

250 m / s