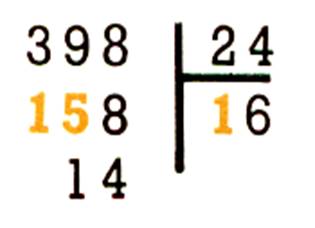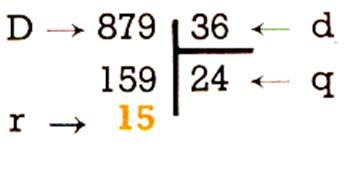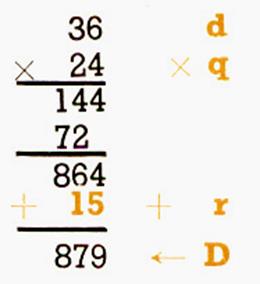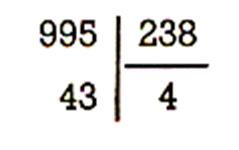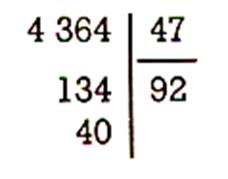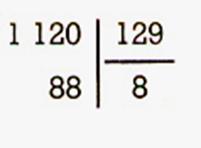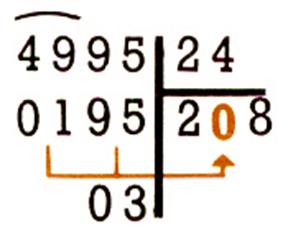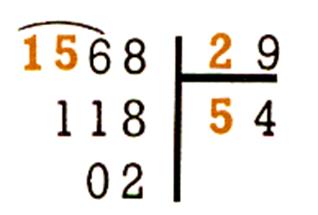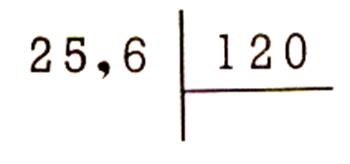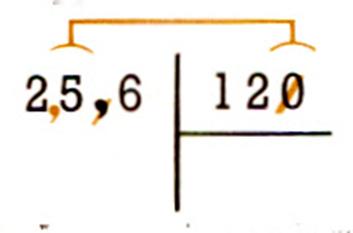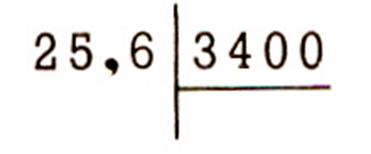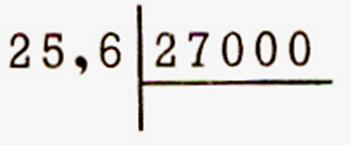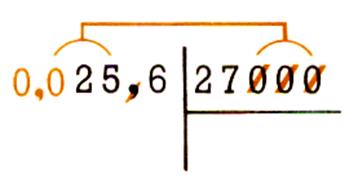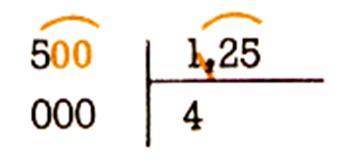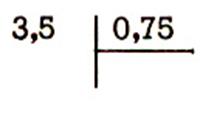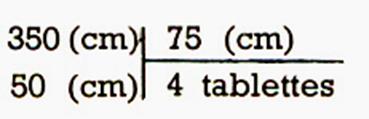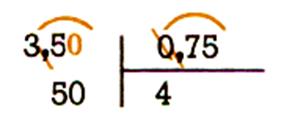Pratique : pour un grand dividende , on fait des divisions successives en commençant par la gauche , et en abaissant 1 chiffre à droite de chaque reste , jusqu’à épuisement des chiffres du dividende .

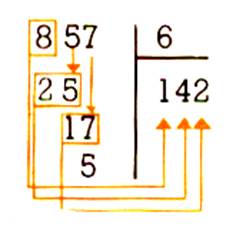
Dans « 8 » il y a 1 fois 6 ;6 ôté de 8 reste 2 , j’abaisse le 5 .

Dans 25 il y a 4 fois 6 soit 24 , 2’ ôté de 25 reste 1 , j’abaisse le 7 .

Dans 17 il y a 2 fois 6 soit 12 , 1é ôté de 17 reste 5 .

Donc 857 : 6 = 142 , il reste 5

div3

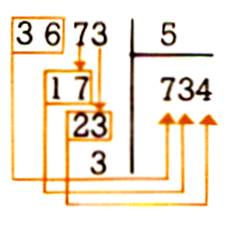
Dans 3 il y a 0 fois 5 , on prend alors 6.

Dans 36 il y a 7 fois 5 soit 35 , ôté de 36 il reste 1, j’abaisse le 7.

Dans 17 il y a 3 fois 5 soit 15 ôté de 17 il reste 2 , j’abaisse 3 ;

Dans 23 il y a 4 fois 5 soit 20 , ôté de 23 il reste 3.

div2

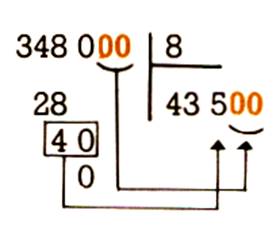
ATTENTION ! quand le dividende est terminer par un ou des zéros.

Quand le dividende est terminer par un ou des zéros que l’on utilise pas , il ne faut pas oublier de les inscrire à droite du quotient.

div1

2° Dividende décimal ; zéro au décimal

Situation 1:

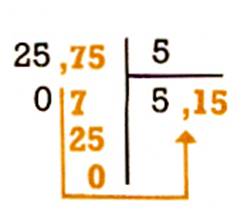
On a payé 25 € pour 5 kg de chocolat ; quel est le prix du kg de chocolat .

On effectue : 25,75 : 5 = 5,15 €

div5

Situation 2 :

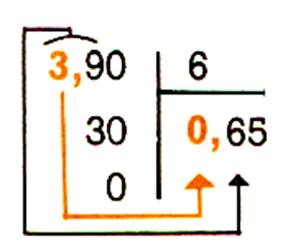
Pour faire une étagère , on coupe en 6 morceaux égaux une planche de 3,90 m ; Quelle est la longueur d’un morceau ?

On effectue : 3,90 : 6 = 0,65 m

Ou 390 cm : 6 = 65 cm

Remarque : si la partie entière du dividende est inférieur au diviseur , on remplace la partie entière du quotient par 0.

div4

Règle : On fait la division comme à l’ordinaire , mais on place une virgule au quotient dès qu ‘ on abaisse le premier chiffre décimal du dividende.

(*le premier chiffre décimal est le premier chiffre après la virgule)

Si la partie entière du dividende est inférieure au diviseur , on remplace la partie entière du quotient par un zéro .

3°)Le Diviseur est terminé par des zéros

Situations :

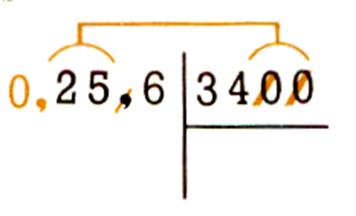
674 000m : 4 000, c’est comme 674 km : 4 ® 674 000 : 4 000

75 850 cm : 600 , c’est comme 758,5 m : 6 ® 758,50 : 600

54 986 litres : 700 , c’est comme 549,86 : 7 ® 549,86 : 700

Règle : Quand le diviseur est terminé par des zéros , on les supprime , à condition d’en supprimer autant au dividende , ou de séparer par une virgule autant de chiffres à droite du dividende qu’il y a de zéros au diviseur.

4°) Diviseur à plusieurs chiffres .

Situation : Combien peut-on remplir de boîtes de 24 œufs , avec 398 œufs ?

Combien de fois 24 dans 398 ?

C’est 398 : 24.

Dans 39 dizaines il y a 1 fois 24 ;ôté de 39 il reste 15 diz. ;

En 158 unités , il y a 6 fois 24 soit 144, ôté de 158 il reste 14 ..

div13

Pratique : Je dis : en 39 combien il y a de fois 24 , ou en 3 (centaines) combien de fois 2 (au diviseur)® 1 fois , 1 fois 24 = 24 , ôté de 39 ® 15. J’abaisse le 8 . En 158 combien de fois 24 , ou en 15 combien de fois 2 , 6 fois ( essai de 7® résultat inacceptable) 6 fois 24 = 144 , ôtés de 158 ® reste 14.

Résultat : on emplit 16 boîtes ; il reste 14 œufs non logés.

5°) Division : reste ; preuve

Examinons la division 879 : 36

Dividende D ® 879

Diviseur d ® 36

Quotient q ® 24

Reste r ® 15

div12

Dans 879 , il y a 24 fois 36 , et le reste 15 ( plus petit que le diviseur )

879 = 36 24 + le reste 15

On peut faire la preuve de la division en multipliant le diviseur par le quotient et en ajoutant le reste au produit obtenu : on doit retrouver le dividende .

div11

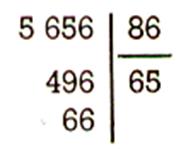
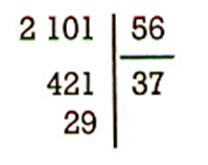
Exercices : Vérifier par la preuve que les divisions suivantes sont exactes .

6°) zéros au quotient :

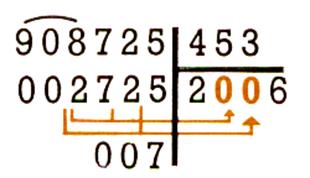
Si on ne peut pas diviser après avoir abaissé un chiffre , on écrit 0 au quotient et on abaisse le chiffre suivant ; si c’est la dernière division partielle , il n’y a plus rien à abaisser : n’oublions pas le 0 des unités du quotient .

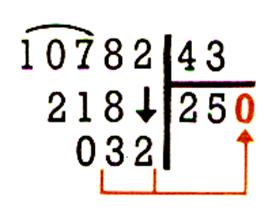
32 diviser par 43 est la dernière division partielle : il n’y a plus rien à abaisser on écrit 0 comme unité des unités du quotient .

7°) Essais et retenue pratique

La division de 15 par 2 donne 7 , mais 29 7 = 203 ne peut être ôté de 156.

Essayons 6 ;

29 6 = 174 ; qu’on ne peut ôté de 156 . 5 convient

car 29 5 = 145 , que l’on peut ôter de 156 …..

div14

Quand le 2^e chiffre du diviseur marque un nombre élevé , la retenue oblige à des essais :

1° examiner ce 2^e chiffre ; 2° gagner du temps en essayant mentalement le chiffre du quotient .

Partie II

8°) dividende et diviseur entier :quotient décimal ou approché ;

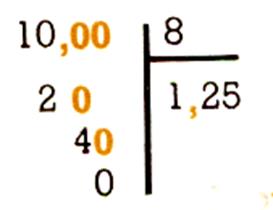
Situation problème : On a fait 8 serviettes de bain dans 10 m de tissu éponge .

Quelle est la longueur d’une serviette ? c’est 10 m : 8 = 1,25 m

Le quotient 1 n’est pas assez approché : on poursuit la division comme s’il y avait une partie décimale au dividende , en abaissant des zéros .

(voir :dividende décimal N°2 )

div21

9°) dividende et diviseur entier :quotient approché ;

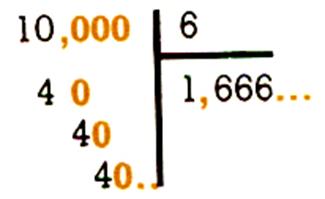
situation : si l’on avait voulu faire 6 serviettes dans la même bande de 10 m , quelle aurait été la longueur d’une serviette ?

L’opération n’a pas de fin : on l’arrête où l’on veut , selon la précision que l’on veut obtenir . On dit qu’on calcul un « quotient approché » , à 1 dixième , 1 centième , 1 millième près …. Ici , où peut-on s’arrêter : au cm ? au mm ?

div20

10 ° ) Quotient inférieur à 1 :

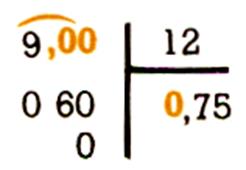
On a fait 12 torchons avec 9 m de toile : quelle est la longueur du torchon ?

C’est 9 m : 12 = 0,75 m

Quand le dividende est inférieur au diviseur , le quotient est inférieur à 1 ;on remplace sa partie entière par un zéro.

div19

Les essais successifs obligent parfois à écrire d’autres zéros avant le premier chiffre significatif

div18

11°) Dividende décimal ; diviseur entier suivi de zéro

Déjà abordé : diviseur terminé par des zéros

Examiner les divisions suivantes : On supprime les zéros du diviseur , à condition de reculer la virgule du dividende d’autant de rangs vers la gauche qu’on a supprimé de zéros au diviseur.

div36

div35

div33

div34

div32

div31

12°) évaluation du reste.

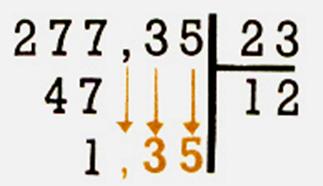
Calcul à 1 unité près du quotient de 277,35 m par 23

Le reste apparent est 1

Le reste réel est 1,35 m

div30

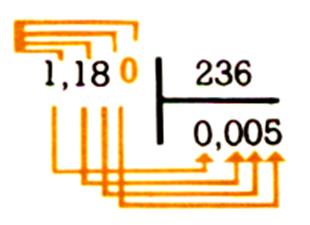
Quand une division n’est pas « poussée » , le reste qu’elle peut comporter doit être complété en considérant le dividende réel.

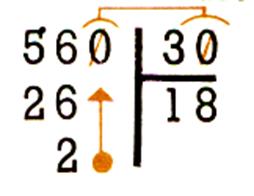
Problème . Combien peut-on tirer de réglettes de 30 cm dans une baguette de bois de 5,6 m ? Y a t- il un reste inutilisé ? Quelle est sa mesure ?

5,6 m = 560 cm

On fait 18 réglettes , il reste 2 ;

dites 2 de quoi ?

div29

13°) Diviseur décimal

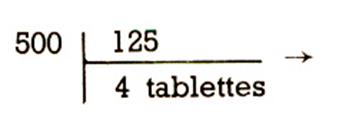
situation 1 :

Combien fait-on de tablettes de 1,25 m dans une planche de 5 m ?

Je peux dire : combien de tablettes de 125 cm dans une planche de 500 cm

5 : 1,25

div27

div26

125 cm 4 = 500 cm

situation 2 :

Combien de tablettes de 0 ,75 peut-on tirer d’une planche de 3,5 m ?

div24

div23

div25

350 cm = 75 cm4 + 50 cm ( reste ) ; 3,5 m = 0,75m 4 + 0,75 m (reste)

Remarque : en multipliant le dividende et le diviseur d’une division par un même nombre ( 10 ; 100 ;1000) on ne change pas le quotient.

( voir : transformer une écriture fractionnaire en fraction)

Règle : Quand un diviseur est décimal , il faut le rendre entier en barrant la virgule , ce qui le rend 10 ; 100 ; 1 000; ….fois plus grand . On doit alors rendre le dividende 10 ; 100 ; 1000 ; fois plus grand , en écrivant des zéros à sa droite , s’il est entier , ou en déplaçant sa virgule de 1 ; 2 ; 3 ; ….rangs vers la droite ( on y inscrit des zéros si c’est nécessaire)

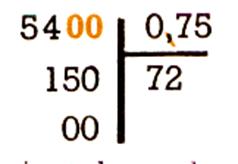
14°) Diviseur décimal inférieur à 1

Combien emplit – on de bouteilles de 0,75 litres avec le vin d’un tonneau de 54 litres ? 54 : 0,75 = 72 bouteilles .

Remarque . quand le diviseur est inférieur à 1 , le quotient est supérieur au dividende .

div22

En effet , le tonneau contient 54 fois 1 litre , il contient donc plus de 54 fois une quantité inférieure à un litre .

Remarque :

On peut détourner la difficulté : dans 1 litre il y a 100 centilitres ; dans 54 litres il y a 5400 cl ; dans une bouteille il y a 75 cl ( une bouteille contient 3/4 litre).

Aussi on peut remplacer la division 54 : 0,75 par la division 5400 : 75 =

Le résultat recherché ( que l’on appelle « quotient » ) reste le même : 72

On devra vérifier si le calcul est exact en faisant la multiplication 75 par 72 , on doit obligatoirement trouver « 5400 ».

CONTROLE:

- 1

EVALUATION:

Appliquons les règles de disposition étudiée :

Sans les compter , disposer les divisions ci –dessous comme si vous alliez les faire , en modifiant comme il faut les deux termes .

A) Diviseur terminé par des zéros ( SOS rappels1 et rappels 2 )

	a	b	c	d	e
1	7800 : 350	5400 :3500	67800 :5400	78500 :480	37400 : 4300
2	7492 : 430	6785 :2500	475 :7200	3750 :5800	67900 :75000
3	578 : 23000	25 :7800	432 :85000	8 : 650	92 :33000
4	83,5 : 420	267,5 :500	483,5 :37000	74,25 :2400	5,95 : 800

B) Diviseur décimal . ( SOS rappels 1 et rappels 2 )

	a	b	c	d	e
1	495 :7,5	83 :4,25	74 :1,432	239 :0,52	425 :0,075
2	53,8 : 2,5	7,459 :3,85	6,387 :0,25	0,485 : 2,65	0,98 :0,03
3	24,3 :5,75	86,2 :3,54	7,08 : 0,325	6,5 : 0,042	9,35 : 2,008

ATTENTION aux zéros inutiles, à supprimer d’abord :

C
	475 : 3,50	7430 : 2,700	49,5 : 380	35,06 :0,950	2,48 :0,6340

Recopier les divisions suivantes , telles quelles , faîtes au crayon les modifications utiles ; puis effectuer le calcul en ligne sans poser l’opération.

D
	738 : 60	123,2 : 0,8	1778 : 700	58,05 :0,9	0,75 : 0,06

APPLIQUONS dans les exercices suivants les règles étudiées en détail :

Effectuer , après avoir supprimé des zéros inutiles :

E
	17,28 : 3,60	28,416 : 4,800	486 : 7,20	11,80 : 0,800	134,90 :4,750

Calculer le quotient exact ( ici , c’est un quotient entier)

F	a	b	c
1	17 776 : 47	162 :3,6	122640 : 560
2	544 : 8,50	136 620 : 92	200 600 : 2 950

Suite

	a	b	c
1	54 810 : 58	507 : 7,8	74 292 : 82
2	448 812 : 548	690 : 3,75	479 610 : 730

Calculer le quotient exact ( ici , c’est un quotient entier ou décimal )

G	a	b	c
1	4 576 : 47	26,1 : 5,80	450 : 72
2	281 ,52 : 36	475,3 : 98	2 205 : 840

Calculer le quotient entier ( précisez le reste )

H	a	b	c
1	9 845 : 47	452,8 : 8,6	352 000 : 720
2	61 748 : 294	971 700 : 3 800	684,85 : 5,2

Calculer le quotient approché :

K		a	b
1	à 0,1 près	65 420 : 480	3742,9 : 517
2	à 0,01 près	6 853 : 495	19,2 : 3,820
3	à 0,001 près	1 867 , 8 : 590	18 : 0,687