Aller vers lire….la numération , ne pas confondre : «  nombre » et  « grandeur »

Pré requis:

Numération : base 10
Nomenclature	5
Mettre un nombre entier sous forme de fraction	125
Division de N par 10 ; 100 ;1000	25

ENVIRONNEMENT du dossier:

			Classe de 6^ème
Index warmaths	Objectif précédent : 1°) le nombre entier 2°) Notion et idée du nombre décimal . 3°) La fraction décimale 4°) le nombre décimal et le système décimal.	Objectif suivant 1°) Numération des nombres décimaux. 2°) Classification des nombres décimaux 3°) Cours : Calculs sur les décimaux au collège.	Tableau : 37a : 1°) Etablissement du système décimal en primaire. Liste des activités « cours » avec les nombres décimaux 3°) Voir la liste des cours sur le calcul numérique.

Fiche de travail sur LES NOMBRES DECIMAUX et LE SYSTEME METRIQUE

	1°) Nombres décimaux
	2°) SYSTEME METRIQUE.
	3°) Comparaison de décimaux.
	4°) Méthode pratique de comparaison de décimaux .
	Exercices .
	5°) Encadrement ordre de grandeur.
TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité 35a Devoirs	Corrigé Contrôle	Corrigé évaluation
				>>> Liste de fiches de travaux sur les décimaux	ICI : CORRECTION des travaux .

COURS

1°) Nombres décimaux
Dans le cours précédent « mesure de longueur de segment  » , on a utilisé des nombres à virgule.
On les appelle des nombres décimaux car ils sont obtenus grâce à des subdivisions qui vont de 10 en 10.
Ici « la partie entière »	736	,	467	Par ici « partie décimale »
Dans le tableau ci-dessous , on vous demande de placer convenablement les chiffres des décimaux suivants : «  51 907,75 » ; «  0 , 005 743 » ; «  8462 » ; on a déjà placé «  736 , 467 »

Ci-dessous : Tableau classant les parties décimales d’un nombre « décimal »

Partie entière du nombre décimal.							Partie décimale du nombre décimal.
centaines de mille	dizaine de mille	Unités de mille	centaines	dizaines	Unités	virgule	dixièmes	centièmes	millièmes	dix millièmes	Cent millièmes	millionièmes
			7	3	6	,	4	6	7
	5	1	9	0	7	,	7	5
					0	,	0	0	5	7	4	3
		8	4	6	2

Info ++

« 537,482 » peut se lire « 53748,2 centièmes» , «  537 482 millièmes » ou encore : 5 centaines 3 dizaines 7unités 4 dixièmes 8 centièmes 2 millièmes. On vous demande de lire (oralement ) les nombres que vous avez écrit dans le tableau.

Activité : Quel est le chiffre des millièmes de 67 905,39 ? ………???…….. ; Quel est le chiffre des dixièmes de 3 914 ? ………???……..

Remarque : · On obtient une autre écriture d’un nombre décimal en mettant des « 0 » à la droite de la partie décimale . Ainsi : « 13,57 ; 13,570 ; 13, 570 00 » sont des écritures équivalentes , ce sont « 3 » écritures d’un même décimal. « 13,57 » en est l’écriture réduite ( il n’y a pas de « 0 » (zéro) superflus). · Tout entier peut être considéré comme un décimal dont la partie décimale n’est faite que de « 0 » ( zéros) . Ainsi : prenons « 17 » : « 17,0 » ; « 17,00 » , « 17,000 » sont trois écritures de l’entier « 17 »

Nous reprenons la portion de graduation vu au chapitre « mesure de longueur –mesurage et décimaux »

Compléter le graphique en donnant pour chaque nombre une écriture avec deux chiffres après la virgule.

Activités :

Exercice 1 : Donnez des nombres suivants une écriture avec 3 chiffres après la virgule.

43,720

0,460

18,300

7, 000

45,700 0

0,030

89, 000

150,000

Exercice 2 : Donnez l’écriture réduite des nombres suivants :

57,430

18,00

0,600 0

5,037

0,004 0

450,000

Exercice 3 : Placer sur la droite graduée les nombres « 2,3 » ; « 4,8 » ; « 0,4 » ; « 3,25 » ; « 0,75 » ; « 5,67 » ;  « 0,08 » ; « 1,11 »

Info ++

2°) SYSTEME METRIQUE.

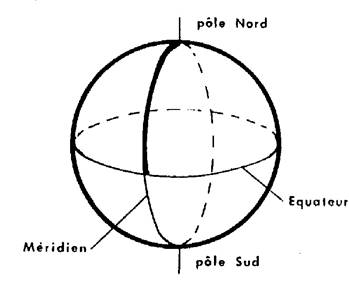
L’unité légale de longueur en France et dans presque tous les pays du monde est le « mètre » Le mètre a été déterminé à la fin du XVIII^ème siècle par des savants français. C’est environ la dix millionième partie du quart du méridien terrestre. (cercle complet ) C'est-à-dire que la longueur du tour de la terre est environ …???………..……m)

Unité

Symbole

Correspondance avec le mètre.

Les multiples

Kilomètre

km

1 km=…………….m

1 m=…………….km

Hectomètre

hm

1 hm=…………….m

1 m=…………….hm

Décamètre

dam

1 dam=…………….m

1 m=…………….dam

Mètre

m

Les sous – multiples

Décimètre

dm

1 dm=…………….m

1 m=…………….dm

Centimètre

cm

1 cm=…………….m

1 m=…………….cm

Millimètre

mm

1 mm=…………….m

1 m=…………….mm

Attention

On écrit « 2,35 m » et non pas «  2 m,35 » ( ni « 2,35 m. » ; ni « 2,35 ms » ; ni «  2,35 M ») Parmi les longueurs suivantes, certaines sont mal écrites . Barrez –les

Activité :

1. Exprimer en m la longueur définie par 7 km 2 hm 5 dam 4 m :

???

2. Exprimer en mm la longueur définie par 5 m 1 cm 3 mm :

???

3. Exprimer en dm la longueur définie par 1 dam 2 m 9 dm 5 cm 6 mm :

???

Changement d’unité – conversion :

Tableau

Info ++

km

hm

dam

m

dm

cm

mm

8

7

4

3

5

Dans le tableau ci-dessus , on a placé un nombre :

On peut lire indifféremment : 874,35 m ou 87 435 cm ou 87,435 dam Donnez les autres possibilités :

En km = ???

En hm =???

En dm =???

En mm =???

Exercices ; série 2 :

En plaçant dans le tableau les nombres ci-dessous , faîtes les conversions :

58,76 dam = ?

m =???

km = ???

mm =???

0,4893 hm = ?

cm = ???

km =???

dm =???

Exercices ; série 3 : Vous devez être capable de faire les conversions sans utiliser le tableau :

64 km =???

dm

21,67 m =???

km

45,6 dam =???

cm

0,57 dm =???

mm

9740 mm = ???

hm

0,004 35 hm = ???

cm

34 cm = ???

m

75,48 mm = ???

dam

13,87 dm= ???

km

73 000 dam = ???

dm

3°) Comparaison de décimaux.

Exemple : On voudrait comparer «  7, 354 » et « 8,79 » Imaginons que «  7, 354 » et « 8,79 » sont des mesures de longueurs en mètres . Si on les exprimes en « mm » ,on obtient respectivement «  7 354 » et « …???. »

«  7, 354 » «  7 354 » « 8,79 » « ………….. »

Puisque 7 354 < 8 790 on peut écrire : 7 , 354 < 8 , 790

Remarque : Au lieu de parler de mesure de longueur, on peut dire ( voir le chapitre 1) : «  7, 354 » correspond à «  7 354 millièmes » et « 8,79 » correspond à « ??? millièmes »

Autre méthode : O peut utiliser une droite graduée .

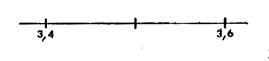
Placez les points correspondant à «  7, 354 » et « 8,79 ». Sur la droite , les nombres sont placés dans l’ordre croissant de la gauche vers la droite. Alors «  7, 354 » …???… « 8,79 ».

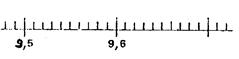
Autre exemple : on voudrait comparer « 9,7 » et « 9,54 » . Imaginez un même changement d’unité pour les 2 nombres afin d’obtenir des entiers. (il faut décaler la virgule de « ??? » rangs pour chacun des nombres.)

« 9,7 » 970 « 9,54 » 954

Puisque ??? … 954 on écrit : « 9,7 » ??? « 9,54 » ; placez ces 2 nombres sur le dessin ci-dessus !!!

Info ++

4°) Méthode pratique de comparaison de décimaux .

Info +++

De deux décimaux qui n’ont pas la même partie entière ,le plus grand est celui qui à la plus grande ………..….

Exercice : Rangez dans l’ordre croissant :

3

8,73

1

7,96

42,7

0,962

134,7

2,9856

Réponse :

Pour comparer deux décimaux ayant la même partie entière , il suffit de comparer les chiffres de même rang des parties décimales

C’est ce que nous allons voir dans les cas ci –dessous : ( vérifiez en plaçant les nombres sur la droite graduée proposée dans chaque exemple )

· Comparons « 17,67 » et « 17,82 » « 17,67 » « 17,82 » Puisque 6 < 8 Alors « 17,67 » ??? « 17,82 »

· Comparons « 3,57 » et « 3,5 » « 3,57 » « 3,50 » Puisque 0 ??? 7 Alors « 3,57 » ??? « 3,5 »

· Comparons « 0,2 » et « 0,089 » « 0,200 » « 0,089 » Puisque 2 ??? 0 Alors « 0,2 » ??? « 0,089 »

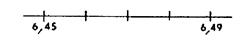
· Comparons « 547 » et « 547,3 » « 547 » peut s’écrire « ????? » « 547,3 » Puisque 0 ??? 3 · Alors « 547 » ??? « 547,3 »

· Comparons « 6,49 » et « 16,4903 » « 6,49» peut s’écrire « 6,4900 » « 16,4903 » Puisque 0 ??? 3 · Alors « 6,49 » ??? « 16,4903 »

· Comparons « 0,009 » et « 10,01» « 10,01» peut s’écrire « 10,010» « 0,009  » Puisque 1 ??? 0 Alors « 0,009 » ??? « 10,01»

Remarques : 1°) Il est toujours possible de comparer deux décimaux (différents) 2°) Comme avec les entiers, on peut utiliser les signes : et ou 3°) Les propriétés des inégalités sont les mêmes pour les décimaux et pour les entiers. On peut aussi écrire des doubles inégalités avec des décimaux.

4°) Exercices :

Série 1 : Mettre le symbole convenable ( < ou > ) entre les nombres suivants :

123,13 ……???….89,789

3,46 ………???…. 3,461

5,6388……???……5,7

1,10………???…….0,998

547,17 …???……547,1249

0,543……???…..0,61

O,15 …???…….0,073

0,0009 …???…0,01

Série 2 En utilisant le signe «  » rangez dans l’ordre croissant :

0,86

0,015

14,81

0,0097

8,54

17

0,089

28,74

14,53

28,547

0,799

Info ++

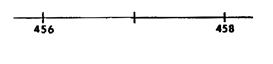
Série 3 Ecrivez la liste des décimaux compris entre « 5,27 » et « 5,82 » qui s’écrivent avec un chiffre après la virgule. ( On dit aussi « ayant une décimale »)

???????????????????????????????

Placez ces nombres sur la droite graduée , ainsi que « 5,27 » et « 5,82 »

Info plus

5°) Encadrement - ordre de grandeur.

Comme pour les entiers , on peut donner des encadrements de nombres décimaux.

Ainsi : 42 < 42,67 < 43 est un encadrement de 42,67 par 42 et 43 ; ( on dit aussi que : 42,67 est comprit entre les deux nombres entiers 42 et 43 ) On dit aussi : que l’on a « encadré » « 42,58 » par les deux entiers consécutifs … ??????? ..et … ?????????… « 42 » est la valeur approchée à 1 prés par défaut de « 42,58 » ( c’est la partie entière immédiatement inférieure ) « 43 » est la valeur approchée à 1 prés par excès de « 42,58 » ( c’est la partie entière immédiatement supérieure) )

Exercices : Donnez les encadrements des nombres ci-dessous par des entiers consécutifs.

…… ????……..< 5,2 < …… ?????…

… ????……..< 0,537 < …… ???…

… ????……..< 19,33 < …… ???…

… ????……..< 0,07 < …… ???…

Info ++

· On peut donner des encadrements par des dizaines , des centaines consécutives …etc. : exemple : 6 000 < 6267 , 48 < 7 000 « 6 000 » est la valeur approchée à 1 000 prés par « défaut » de « 6267 , 48 » « 7 000 » est la valeur approchée à 1 000 prés par « excès  » de « 6267 , 48 » On dit aussi que « 6 000 » est un ordre de grandeur de « 6267 , 48 » ( on dit aussi : « arrondi » ) Si on veut être plus précis , on peut donner d’autres encadrements : · 6 200 < 6267,48 < 6 300 ( valeurs approchées à 100 prés ) · 6 260 < 6267 , 48 < 6 270 ( valeurs approchées à ?????? )

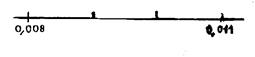
· On peut donner des encadrements par dixièmes , par centièmes consécutifs ….etc. Exemple : 0,007 < 0,00743 < 0,008 « 0,007 » est la valeur approché à 0,001 prés par défaut de « 0,00743 » « 0,008 » est la valeur approché à 0,001 prés par excès de « 0,00743 »

Exercice 2 : Donnez la valeur approchée à 0,01 prés par défaut de 0,8752 : ????? Donnez la valeur approchée à 0,1 prés par excès de 5,263 : ????

Remarque : Très souvent, pour donner un ordre de grandeur , on choisira une valeur approchée dont tous les chiffres sont nuls sauf un. Exemple :

634,41 600

54, 373 50

0,041 0,04

Si le nombre est le plus prés de sa valeur approchée par excès , on choisira celle-ci :

4 987,67 5 000

1,81 2

0,00763 0,008

TRAVAUX AUTO FORMATIFS (devoir formatif)

CONTROLE :

Voir à l’intérieur de la fiche

EVALUATION

Faire les exercices du cours