|
Auteur : WARME R. DOSSIER : Elève
DOCUMENT
« ELEVE » .
|
||
|
NOM : ……………………………… |
Prénom : ………………………….. |
Classe :………………….. |
|
Année
scolaire : ……………………… |
Dossier pris le : ……/………/……… |
Validation de la
formation : O - N
Le :
…………………………………….. Nom du
formateur : …………………… |
|
ETABLISSEMENT : ………………………………………….. |
||
Préambule :
( cliquez ici :
activités pré requises)
INFORMATIONS : Dans un triangle si l’on connaît 3 mesures sur 6 , on peut découvrir ou retrouver les 3
mesures .
Les
mesures d’un triangle sont :
3 mesures de longueur et 3 mesures d’ angle.
A ) « résoudre
un triangle » scalène :
Ainsi
« résoudre un triangle » c’est rechercher les « 3 » mesures
manquantes , à partir des trois mesures données..
|
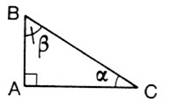
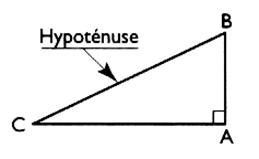
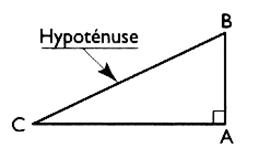
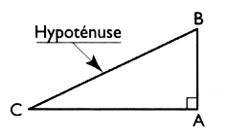
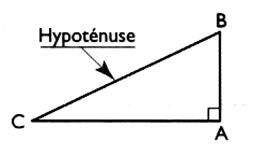
Résoudre un triangle rectangle : Les caractéristiques du triangle rectangle sont : 1°) 3 longueurs : ce sont les longueurs des
côtés , dont une s’appelle « hypoténuse ». . 2°) 3 angles : l’angle « alpha » et l’angle
« bêta » et un angle
particulier « un l’angle droit ». |
|
B )
Méthodes de résolution d’ un triangle :
Pour
résoudre un problème sur le triangle il y a deux méthodes :
-
par le graphique : On tracera le triangle à
partir des 3 caractéristiques connues.
-
par le calcul et suivant les données :
a) pour ce qui concerne les angles on fera
appelle aux relations trigonométriques ( sinus ; cosinus ; ……)
b) pour ce qui concerne les longueurs des côtés
on utilisera dans entre autre « Pythagore » ; ….
c) Citer les
possibilités permettant d ’ identifier les caractéristiques d’ un
triangle rectangle (mesures d’angle et de longueurs) par le calcul.
1°) Cas du triangle dont on
connaît 3 côtés (3 dimensions = 3 longueurs)
:
on
recherche alors la valeur des 2 angles « inconnus » .
a) Si le triangle est rectangle :
on utilisera les
relations trigonométriques .
on fera appelle à la
relation concernant la somme des angles
dans un triangle. ( complémentaires et ou supplémentaires)
b) Si le triangle n’est pas un triangle
rectangle , (ni équilatéral ; ni isocèle ) on appliquera les relations
sur les triangles quelconques
. : difficulté qui n’est pas au programme du CAP
( mais
éventuellement : voir Infos : ( niveau
V : BEP ou niveau
IV : relations métriques dans le triangle quelconque)
2°) Cas du triangle dont on
connaît 2 côtés (2 longueurs) et un
angle ( en degré) :
a) le triangle
est un triangle rectangle : (on peut le tracer)
- le triangle est rectangle et l’angle
connu est = 90° ; on fera « Pythagore ». pour trouver le 3ème
côté .
ensuite : on appliquera les relations trigonométriques
dans le triangle rectangle pour trouver le deuxième angle , on en déduira le
troisième ( on connaît ou on se souvient de la relation concernant les angles
complémentaires et supplémentaires)
3°) Cas du triangle dont
on connaît 2 angles et un côté :
On peut en
déduire le troisième angle .
a) le triangle
est un triangle rectangle : (on peut
le tracer)
- si le triangle est rectangle ( l’angle connu = 90°)
on en déduira le troisième ( on connaît ou on
se souvient de la relation concernant les angles complémentaires et
supplémentaires)
b) si le triangle est quelconque : (à voir au
niveau IV)
|
Leçon |
Titre |
|
N°20 |
PYTHAGORE : Le théorème ; la Propriété de PYTHAGORE et sa
réciproque. |
CHAPITRES
|
|
|
|
C ) Applications
particulières :
recherche d’une diagonale et hauteur . |
|
|
III ) CACULS : recherche d'une longueur d'un côté connaissant les longueurs des autres côtés ( les 3 cas ) . |
|
|
|
|
|
COURS |
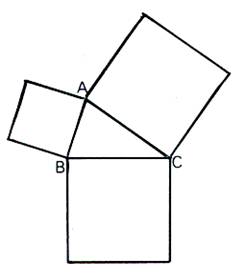
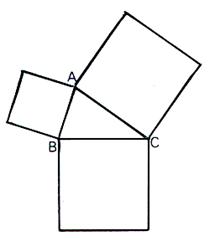
i Pour démontrer le théorème de Pythagore ,
Euclide démontre que :
|
Si l’aire du carré ayant comme côté l ’ hypoténuse BC est égale à la somme de l’aire du carré
de côté AB et l’aire du carré de côté AC : on aura démontré que
BC2 = AB2 + AC2 |
|
FActivités
permettant de mettre en évidence le théorème de Pythagore :
1°) Découper 8 triangles rectangles ayant comme
côtés de l’angle droit , 3 cm et 4 cm .
Mesurer la longueur de l’hypoténuse : ( 5 cm)
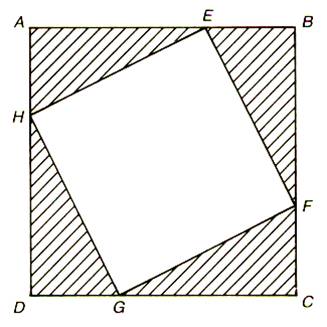
2°) Tracer un carré initial de 7 cm par 7 cm .
|
C2 Quelle est la
surface restante , dans le carré initial ? De quelles
figures se compose – t – elle ? Elle se compose de 2 carrés. C 1 et
C 2 Calculer les aires de ces carrés . Faire la somme
des aires. |
C
1 |
Réponse : ( le carré) ; un carré de 3cm de côté (C1
aire = 9 cm² )et un carré de 4 cm de côté ( C2 aire = 16 cm²) , C1 + C2 = 4 +
16 = 25 cm²).
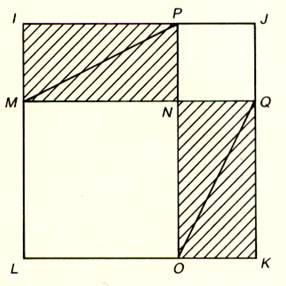
3°) Tracer un second carré initial de 7 cm par 7 cm .
|
Au quatre coin
du carré initial disposer les 4 autres triangles rectangles découpés , comme
l’indique le pointillé. Quelle est la
figure formée par les 4 hypoténuses ? Pourquoi ? Calculer
l’aire de C3 . Quelle
peut-être les conclusions ? |
C3 |
Réponse : (la figure est
le carré de 5 cm sur 5 cm ; l’aire de C3 = 25 cm²) ;
En conclusion. On remarque que la somme des aires des deux carrés (
C1 et C2) formés
par les côtés de l’angle droit d’un triangle rectangle est égale à l’aire du
carré ( C3 ) dont la longueur du côté est la longueur de
l’hypoténuse .
4°) En résumé :
Dans un triangle rectangle , le « carré »
…… de l’hypoténuse est égal à la somme des « carrés » ……….. des côtés
formant l’angle droit .
|
B) THEOREME DE PYTHAGORE. |
¨Pour le théorème de Pythagore , on démontre
, comme Euclide que :
|
A partir d’un triangle rectangle ,
l’aire du carré ayant comme
côté l ’ hypoténuse BC est égale à la
somme de l’aire du carré de côté AB et l’aire du carré de côté AC : on peut écrire que BC2 =
AB2 + AC2 De cette
égalité en découle des calculs : Exemple :
si |
|
a A
savoir et retenir : Enoncé du THEOREME de PYTHAGORE :
|
Dans un triangle
rectangle , la somme des carrés des longueurs des côtés de l'angle droit
est égale au carré de la longueur de
l'hypoténuse . |
—Ce qui se traduit :
|
Si le triangle CBA est rectangle en A
alors ….. |
|
…..alors: AB² + AC ²
= BC ² |
|
|
||
Dans un triangle si la somme des carrés des mesures de deux côtés consécutifs est égale au carré
de la mesure du troisième alors ce triangle est rectangle .
Et dire
que
le triangle ABC est un triangle rectangle en A c’est aussi dire
que AB² +AC² = BC²
F Activité :
Construire un triangle A BC
rectangle en A tel que AB = 6 cm ; AC =
8 cm . Mesurer l' hypoténuse [BC] . (c'est
un nombre entier en centimètres) .
Calculer AB² puis AC ² , faire la somme AB² + AC²
, puis calculer BC² . Comparer les deux résultats .
Constater que
AB² + AC² , est égal à BC² .
Enoncé :
|
Si dans
un triangle, lorsque le carré de la
longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés , alors le triangle est rectangle . |
Ce qui se
traduit :
|
Si AB² + AC ²
= BC ² …..alors: |
|
…..alors: le
triangle CBA est rectangle en A alors
….. |
|
|
||
ž . Activité 1
Enoncé : Soit le triangle BAC dont les côtés mesurent
respectivement : 30 ; 40 ; 50 mm ; est - il rectangle ?.
Solution :
- On écrit : le triangle BAC
sera rectangle si CB² = CA² + AB ²
- On calcule les
« carrés » des côtés :
CB² = 50 ² = 2500
CA² = 40 ² = 1600
AB² = 30² = 900
- On calcule la somme des
carrés : CA² + AB² = 1600 + 900
= 2500
- On compare avec CB² .( = 2500 )
On constate
qu’il y a égalité :
Puisque CB² = 2500 et que CA² +
AB² = 2500
- On déclare que la relation CB² = CA² + AB ² est vérifier ;
- On conclut que le triangle BAC est rectangle .
ž . Activité 2
Enoncé : Le triangle BAC dont les côtés mesurent respectivement : 15 ;
20 ; 30 mm ; est - il rectangle .
Solution :
- Le triangle BAC sera rectangle
si CB² = CA² + AB ²
- Calculs :
CB² = 30 ² = 900
CA² = 21 ² = 441
AB² = 20² = 400
- Calcul de la somme CA² + AB² =
441 + 400 = 841
-
on compare le résultat de la somme avec
« CB² »
Puisque CB² = et que CA² + AB² =
841 ; la relation CB² = CA² + AB ²
n' est pas vérifier ;
- conclusion : le
triangle BAC n'est
pas rectangle .
|
III ) CALCULS : recherche d'une
longueur d'un côté connaissant les
longueurs des autres côtés. ( nous traitons les 3
types de problème ) |
A ) recherche de
la longueur de l'hypoténuse
"AB" :
|
[CB] = ? [AB]= 3 [CA]= 4 |
Tracer le triangle rectangle et mesurer BC.!!!!!! Sachant que [AB]= 3 cm et
[CA]= 4 cm |
Calcul de la
longueur du [CB] :
|
Procédure : |
Application |
|
On pose l’
équation : |
BC² = AC² + AB ² |
|
On calcule : AC² ; avec AC = 4 et AB ² ; avec AB = 3 |
AC² = 4 ²
= 16 AB² =
3² = 9 |
|
On effectue la
somme : |
BC² = AC²
+ AB ² BC² = 16
+ 9 BC² = 25 |
|
Calcul de BC : On sait que |
BC = BC = BC = 5 |
Exemple de
présentation des calculs sur feuille de devoir :
On donne : AC = 4 ; AB = 3 ; calculer CB .
Solution :
|
1°) BC² = AC²
+ AB ² 2°) BC² = 16
+ 9 ; BC²
= 25 3°) BC = 4°) BC = 5 |
|
B ) recherche de
la longueur du côté CA :
|
|
On
donne : [CB] = 42 [AB]= 21 [CA]= ? |
Calcul de la
longueur du [CA] :
|
Procédure :
|
Application |
|
On pose : |
BC² = AC²
+ AB ² |
|
On calcule : CB² ; avec CB = 42 AB ² ; avec AB = 21 |
CB² = 42 ²
= 1764 AB² =
21² = 441 |
|
On remplace
les lettres par les valeurs connues : |
BC² = AC² + AB ² 1 764 = AC² + 441 |
|
On transforme
l'égalité: Se souvenir de
la transformation 5
= 3 + 2
; 5 = ? + 2 , pour " ? remplacer le point d'interrogation "on sait que la réponse
est "3" . pour trouver
cette valeur "3" on doit faire la soustraction " 5 - 2 " on opère de la
même façon pour obtenir AC² = ……. |
1 764 = AC² + 441 1 764 - 441 = AC² on peut " retourner" les deux membres. Ce qui donne : AC² = 1 764 - 441 AC² = 1323 |
|
Calcul de AC : On sait que |
Recherche de AC :
avec la
calculatrice on calcule :
AC = 36 , 37 |
En résumé : BC = 42
; AB = 21 ;calculer de AC.
|
1°) BC² = AC²
+ AB ² 2°) 1 764 = AC²
+ 441 3°) AC² = 1 764 -
441 ;
AC² = 1323 4° AC = |
|
C ) rechercher
par le calcul la longueur du côté "AB" :
|
|
On
donne : [CB] = 20 [AB] = ? [CA]= 16 |
Calcul de la
longueur du [AB] :
|
Procédure : |
Application : |
|
On pose : |
BC² = AC² + AB ² ; 20² =
16² + AB² |
|
On calcule : CB² ; avec CB = 20 AC ² ; avec AC = 16 |
- CB² =
20 ² = 400 - AC²
= 16² =
256 |
|
On remplace
les lettres par les valeurs connues : |
BC² = AC² + AB ² 400 = 256 + AB ² |
|
On transforme
l'égalité: Se souvenir de
la transformation 6
= 3 + 2
; 5 = ? + 2 , pour " ? remplacer le point d'interrogation "on sait que la réponse
est "3" . pour trouver
cette valeur "3" on doit faire la soustraction " 5 - 2 " on opère de la
même façon pour obtenir AB² = 400 - 256 . |
400 = 256 + AB ² 400 - 256 = AB² on peut "
retourner" les deux membres. Ce qui donne : AB² = 400 - 256 ( 400 - 256 = 144) AB² = 144 |
|
Calcul de AB : On sait que |
Recherche de AB:
avec la
calculatrice on calcule : AB = 12 |
Exercice résumé :
BC = 20 ; AC =
16 ; calculer AB.
|
Calcul de AB 1°) BC²
= AC² + AB ² ; 20²
= 16² + AB² 2°) AB² = 400 - 256 ;
AB² = 144 3°) AB = 4°) AB = 12 |
|
|
IV) APPLICATIONS DU THEOREME DE PYTHAGORE ET DE SA RECIPROQUE |
|
|
Pour tracer des angles droits , les Egyptiens se servaient d’une
corde fermée à 12 nœuds , régulièrement espacés ; ou
d’un segment de corde à treize nœuds
(régulièrement espacés) dont un nœud à chaque extrémité . Ils la tendaient entre trois
pieux de la façon , un en
« T » ; un en « S » un en « U ». |
|
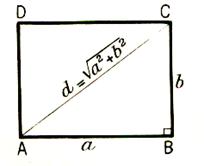
b ) diagonales d’un quadrilatère et hauteur d’un triangle .
|
Diagonale d’un rectangle |
|
|
AC² = AB² + BC². Comme : DB² = DA² + AB² Si « d » = AC ; a =
AB ; b = CB Alors d ² = a² + b² Donc |
|
|
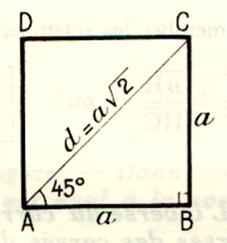
« diagonale du carré = a |
|
|
AC² = DB² = d ² Si AB = BC=CD=DA =
« a » Alors d ² = a² + a² Soit d² = 2 a² Alors
Donc |
|
|
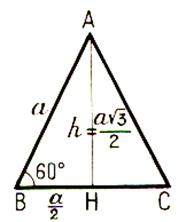
Hauteur du triangle équilatéral =
a |
||
|
a2 = ( a2 - ( a2 - h 2 = h 2 = |
|
|
|
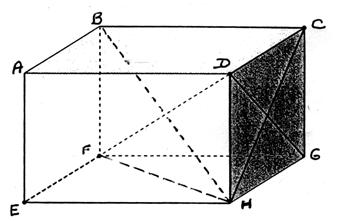
Voir dans
l’espace : on demande de calculer la diagonale d’un
cube , ou d’un parallélépipède rectangle . |
||
|
|
Exemples de demande : -Calculer HC - Calculer FH - Calculer DF |
|
|
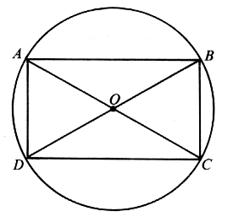
c ) Triangle rectangle inscrit dans un demi -
cercle . |
Rappel : le centre du cercle circonscrit dans un triangle
est se trouve au point d ’intersection
des médiatrices des côtés du triangle .( figure 2)
Observez dans la
figure ci - dessous : en traçant la diagonale AC du
rectangle ABCD , je divise le rectangle en deux triangle rectangle .Si
je trace la seconde diagonale DB , j’obtiens un point O situé à égal distance
des points , A ; B ; C ; D , je peux tracer un cercle passant
par ces 4 points .(figure 1 )
|
Figure 1 |
figure 2 |
|
|
|
l Soit "A" un point quelconque du demi - cercle de diamètre [ B C] .
Si un triangle ABC est
inscrit dans un demi - cercle de diamètre [ B C] alors
ce triangle est rectangle .
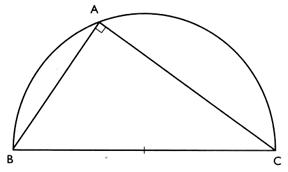
Activité :
Dessiner un demi - cercle de
diamètre BC = 8 cm . Construire un triangle rectangle en A dont le côté de l'angle
droit mesure 3 cm .
Solution :
Pour que le triangle soit rectangle il suffit que le point A appartiennent au cercle
.L'hypoténuse est le segment [ BC
] .
|
On retiendra : Pour identifier un triangle rectangle
, on peut : -
vérifier que ses dimensions satisfont la réciproque de la propriété de Pythagore ; -
vérifier qu'il est inscrit dans un demi - cercle
dont le diamètre est l'hypoténuse du
triangle . vérifier qu'un de ses angles
est droit à l'aide d'une équerre ou un
rapporteur. |
|
N°20 |
sur PYTHAGORE Le théorème ; la Propriété
de PYTHAGORE et sa réciproque. |