|
Doc. CAP ; classe CFA .
Objectifs de ce cours : savoir. |
. |
Pré requis:
|
Lectures
importantes : |
|
|
Les racines
carrées d'une somme et d'une différence. |
|
|
|
|
|
|
|
|
Objectif
précédent : Pythagore : théorème et réciproque. |
Objectif
suivant : |
1°) Tableau : |
|
|
|
|
|
|
DOSSIER : Propriété de PYTHAGORE
et sa réciproque.
|
Autres ++++ |
INTERDISCIPLINARITÉ : voir cas par cas ! ! |
COURS
RAPPELS :
|
1°) Propriété de Pythagore . |
|
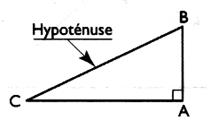
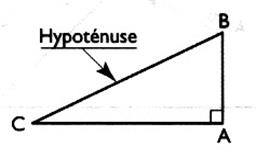
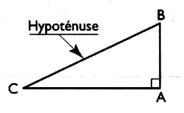
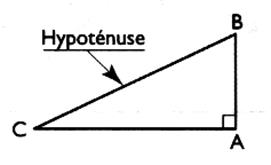
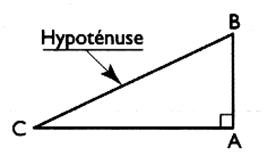
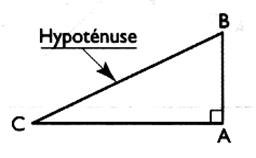
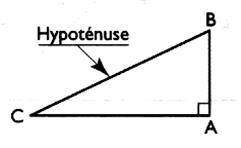
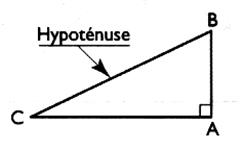
Dans un triangle rectangle , la somme des carrés des longueurs des côtés de
l'angle droit est
égale au carré de la longueur de l'hypoténuse .
|
Si le triangle CBA est rectangle en A alors ….. |
|
…..alors: AB² + AC ² = BC ² |
|
2°) Réciproque de la propriété de Pythagore . |
|
Si dans un triangle , le carré de la longueur d'un côté
est égal à la somme des carrés
des autres longueurs des deux autres côtés
, alors le triangle est rectangle .
|
Si AB² + AC ² = BC ² …..alors: |
…..alors: le triangle CBA est rectangle en A alors ….. |
|
|
Calculs : recherche d'une
longueur d'un côté connaissant les
longueurs des autres côtés . |
Types
de calculs rencontrés : (
ce qui suit aborde les 3 types de problème)
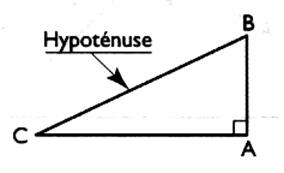
A ) recherche de la longueur de l'hypoténuse AB :
|
|
[CB] = ? [AB]= 3 [CA]= 4 |
Calcul
de la longueur du [CB] :
|
On pose : |
BC² =
AC² + AB ² |
|
On calcule : AC² ; avec AC = 4 et AB ² ; avec AB = 3 |
AC² = 4 ²
= 16 AB² =
3² = 9 |
|
On effectue la somme : |
BC² = AC²
+ AB ² BC² = 16
+ 9 BC² = 25 |
|
Calcul de BC : On sait que |
BC = BC = BC = 5 |
Exemple
de présentation des calculs sur feuille de devoir
:
Résumé : AC = 4 ; AB = 3 ; calculer CB .
|
1°) BC² = AC²
+ AB ² 2°) BC² = 16
+ 9 ; BC²
= 25 3°) BC = 4°) BC = 5 |
|
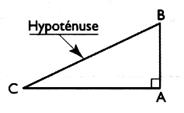
B ) recherche de la longueur du côté CA :
|
|
[CB] = 42 [AB]= 21 [CA]= ? |
Calcul
de la longueur du [CA] :
|
On pose : |
BC² = AC²
+ AB ² |
|
On calcule : CB² ; avec CB = 42 AB ² ; avec AB = 21 |
CB² = 42 ²
= 1764 AB² =
21² = 441 |
|
On remplace les lettres par les valeurs connues : |
BC² =
AC² + AB ² 1 764 =
AC² + 441 |
|
On transforme l'égalité: Se souvenir de la transformation 5
= 3 + 2 ; 5 = ? + 2 , pour " ? remplacer le point d'interrogation "on
sait que la réponse est "3" . pour trouver cette valeur "3" on doit faire la
soustraction " 5 - 2 " on opère de la même façon pour
obtenir AC² = ……. |
1 764 =
AC² + 441 1 764 - 441
= AC² on peut " retourner" les deux membres. Ce qui donne : AC² = 1 764 - 441 AC² = 1323 |
|
Calcul de AC : On sait que |
Recherche de AC :
avec la calculatrice on calcule :
AC
= 36 , 37 |
En
résumé : BC = 42 ;
AB = 21 ;calculer de AC.
|
1°) BC² = AC²
+ AB ² 2°) 1 764 = AC²
+ 441 3°) AC² = 1 764 -
441 ;
AC² = 1323 4° AC = |
|
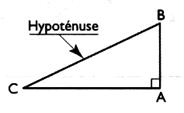
C )
recherche de la longueur du côté
AB :
|
|
[CB] = 20 [AB] = ? [CA]= 16 |
3°)CALCUL de la
longueur du [AB] :
|
On pose : |
BC² =
AC² + AB ² ; 20² =
16² + AB² |
|
On calcule : CB² ; avec CB = 20 AC ² ; avec AC =
16 |
- CB² =
20 ² = 400 - AC²
= 16² =
256 |
|
On remplace les lettres par les valeurs connues : |
BC² =
AC² + AB ² 400 =
256 + AB ² |
|
On transforme l'égalité: Se souvenir de la transformation 6
= 3 + 2 ; 5 = ? + 2 , pour " ? remplacer le point d'interrogation "on
sait que la réponse est "3" . pour trouver cette valeur "3" on doit faire la
soustraction " 5 - 2 " on opère de la même façon pour
obtenir AB² = 400 - 256
. |
400 =
256 + AB ² 400 - 256
= AB² on peut " retourner" les deux membres. Ce qui donne : AB² = 400 - 256 ( 400 - 256 = 144) AB² = 144 |
|
Calcul de AB : On sait que |
Recherche de AB:
avec la calculatrice on calcule : AB
= 12 |
Résumé : BC
= 20 ; AC = 16 ; calculer AB.
|
Calcul de AB 1°) BC²
= AC² + AB ² ; 20²
= 16² + AB² 2°) AB² =
400 - 256 ; AB² =
144 3°)
AB = 4°) AB =
12 |
|
TRAVAUX AUTO FORMATIFS
Enoncé le théorème de Pythagore.
Faire les exercices suivants : (voir le cours pour
le corrigé)
1°)
|
On donne : AC = 4 ; AB = 3 ; Calculer
CB |
|
2°)
|
On donne : BC = 20 ; AC = 16 ; Calculer AB. |
|
3°)
|
On donne : BC = 42 ; AB = 21 ; Calculer de AC. |
|