Retour vers les fiches de travail.

Programme classe de 4^ème

Les parallèles ( définitions)

Classe de 4^ème collège .

Les parallèles : tracés

Les perpendiculaires

Index  warmaths

Objectif précédent 

1°) les angles et les parallèles

2°) Le parallélogramme en primaire.

3°) Cours sur le parallélogramme.

Objectif suivant :

 Suite :Le parallélograme propriétés symétrie centrale ….

1°) Les parallélogramme particuliers

2°) Activités : Tracés

2°)les vecteurs

3°)la translation

1.            Les quadrilatères (Info)

2.          Primaire : info @

Fiche 1 : Propriétés et définitions.

Fiche 2 : Segments joignant les milieux de deux côtés d’un triangle.

Fiche 3 : Comment reconnaître qu’un quadrilatère est un parallélogramme ? .

Fiche 4 : Enoncés réciproques  ( Propriétés ou  théorème )

Fiche 5 : Exemples de recherche et de rédaction de problèmes.

Fiche n°6 :  EXERCICES pouvant être donnés à traiter.

Fiche 7 Exercices sur la symétrie centrale

Collège4ème  :  Travaux fiches sur : Le parallélogramme ( dont les propriétés)

Collège 5^ème  : Travaux fiches sur : Le quadrilatère (dont les propriétés )

TEST

COURS

Devoir  Contrôle

Devoir évaluation

2°) C.C. d’un parallélogramme.

Interdisciplinarité

1. :Fiche de travaux en arithmétique.
2.   Voir : la démonstration en géométrie                 

Corrigé Contrôle 

Corrigé évaluation 

Fiche 1 : Propriétés et définitions.

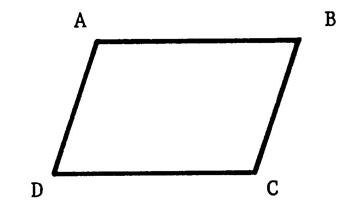
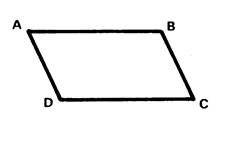
Définition:

On appelle « parallélogramme » tout quadrilatère dont les côtés opposés sont parallèles.

Nous vous récapitulons ici les propriétés  que possède le parallélogramme.

Démontrées ( ou admises  ) en classe de 5^ème et de 6^ème , ces propriétés ne  seront  pas démontrées.

Activité N° ….. :

Complétez les énoncés ci-dessous en vous inspirant de la figure correspondante.

Figures :

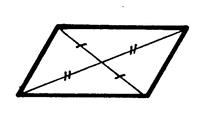
Propriété n°8 :

Si un quadrilatère est un parallélogramme alors ses diagonales se coupent en leur ..milieu…

Propriété n°9 :

Si un quadrilatère est un parallélogramme alors il possède un centre de symétrie qui est le point d’intersection des ..diagonales…

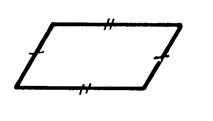
Propriété n°10 :

Si un quadrilatère est un parallélogramme alors ses côtés opposés ont même mesure.

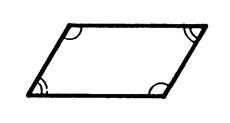
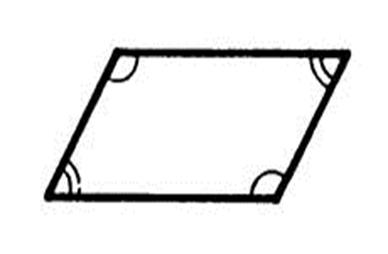
Propriété n°11 :

Si un quadrilatère est un parallélogramme alors ses angles opposés sont égaux  , ses angles consécutifs sont  …supplémentaires ……….

Fiche 2 : Segments joignant les milieux de deux côtés d’un triangle.

Info @......sur les théorèmes des milieux

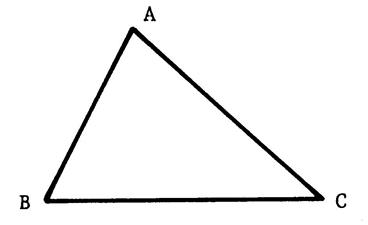
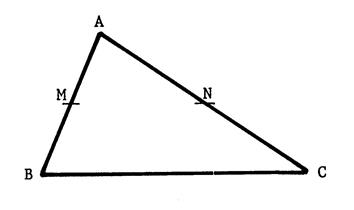
« ABC » est un triangle quelconque.

« M » , « N », « P » sont les milieux respectifs de  [ BC ] , [ CA ] , [ AB ] ,

Nous allons démontrer que  « PN =  »

Par hypothèse :

« M » est le milieu de ……………………..

« N » est le …………………………………

« P » est…………………………………….

Conclusion : « PN =  »

Démonstration :

Dans le triangle « ABC », par hypothèse « P » est le milieu de ……et  « N » est le milieu de …….donc, grâce  au théorème …, ( PN ) ………( BC ) …………….

Dans le triangle « ABC », par hypothèse « N » est le milieu de ……et  « M » est le milieu de …….donc, grâce  au théorème …, ( NM ) ………( AB ) …………….

On vient de dire que  ( PN ) et ( BC) sont parallèles  et que …( NM) et  ..( AB ) … sont parallèles  donc , par définition, le quadrilatère « PNMB » est un …parallélogramme…

Donc , grâce à la propriété n° …. , les côtés  opposés ont  même longueur , donc «  PN = …MB. »

Or, « M » est le milieu de [ BC ]  donc   BM = .

Donc , par transitivité de l’égalité , PN = BM  = .

PN =  .

On prouverait de même que  «  NM = PB »   et   «  MP = BN »

Théorème 3 :

Dans tout triangle , la longueur du segment joignant les milieux de deux côtés est égale à la moitié de la longueur du troisième côté.

Fiche 3 : Comment reconnaître qu’un quadrilatère est un parallélogramme ? .

«  info + @ parallélogramme »

Vous savez qu’un quadrilatère a ses côtés opposés parallèles, alors vous pouvez affirmer grâce à la   ………définition……….que ce quadrilatère est un  ………………..parallélogramme….

Comme activités suivantes, nous allons récapituler différentes façons de prouver qu’un quadrilatère est un parallélogramme.

Ces propriétés ont été démontrées ou admises dans les classes précédentes  ( 6^ème  et   5^ème )  .

Comme ce n’est pas le but de cette fiche , nous ne les démontrons pas ici.

En face des énoncés, en utilisant la propriété correspondante, construisez le point « P » de tel sorte que « APCB soit un parallélogramme.

( laissez les lignes de construction apparentes )

Propriété n°12 :

Si dans un quadrilatère,  les diagonales se coupent en leur milieu alors ce quadrilatère est un parallélogramme.

Propriété n°13 :

Si dans un quadrilatère,  le point d’intersection est centre de symétrie ,  alors ce quadrilatère est un parallélogramme.

Propriété n°14 :

Si dans un quadrilatère non croisé a ses côtés opposés  deux à deux de même longueur ,   alors ce quadrilatère est un parallélogramme.

Propriété n°15 :

Si dans un quadrilatère non croisé a une paire de côtés parallèles et de même longueur ,    alors ce quadrilatère est un parallélogramme.

Propriété n°15 :

Si dans un quadrilatère non croisé a ses angles consécutifs deux à deux supplémentaires ou ses angles opposés deux à deux égaux alors ce quadrilatère est un parallélogramme.

Propriétés caractéristiques.

Etant donné un quadrilatère convexe, les propriétés suivantes sont celles que possède le parallélogramme.

-        Avoir ses côtés opposés parallèles.

-        Avoir ses diagonales qui se coupent en leur milieu.

-        Avoir un centre de symétrie ( le point d’intersection des diagonales)

-        Avoir ses côtés opposés de même longueur.

-        Avoir une paire de côtés parallèles et de même longueur.

-        Avoir ses angles consécutifs deux à deux supplémentaires.

-        Avoir ses angles opposés deux à deux égaux.

Ces propriétés sont donc celles que possède un parallélogramme.

Et qu’il est le seul à posséder.

Elles caractérisent donc le parallélogramme.

On dit que ce sont des propriétés caractéristiques du parallélogramme.

Chacune de ses propriétés pourrait être prise comme « définition » du parallélogramme.

Toutes ces propriétés expriment à leur manière la même propriété :

« le quadrilatère  considéré  est un parallélogramme »

Si l’une de ces propriétés est vraie , les autres sont vraies et si l’une est fausse , les autres sont … fausses….. et alors le quadrilatère n’est pas un ….paralélogramme…..

Dans ces conditions , on dit que ces propriétés sont équivalentes.

Fiche 4 : Enoncés réciproques  ( Propriétés ou  théorème )

Nous allons reprendre la propriété « 8 » et la propriété « 12 » de la fiche 2.

Propriété n°8 :

Si un quadrilatère est un parallélogramme alors ses diagonales se coupent en leur ..milieu…

Propriété n°12 :

Si dans un quadrilatère,  les diagonales se coupent en leur milieu alors ce quadrilatère est un parallélogramme.

Complétez le tableau ci-dessous en écrivant l’hypothèse et la conclusion de ces énoncés.

Hypothèse

conclusion

Propriété n°8 :

Un quadrilatère est un parallélogramme

Si un quadrilatère est un parallélogramme alors ses diagonales se coupent en leur ..milieu…

Propriété n°12 :

Un quadrilatère est un parallélogramme

Si dans un quadrilatère,  les diagonales se coupent en leur milieu alors ce quadrilatère est un parallélogramme.

Pour ces deux énoncés, , vous constatez que :

L’hypothèse de l’un est  ..l’hypothèse . de l’autre.

On dit alors que la propriété « 12 » est la réciproque de la propriété « 8 ».

De même la propriété « 8 » est la réciproque de la … propriété « 12 »….

( elles sont réciproques l’une de l’autre )

Remarque : Pour deux énoncés  de la forme  si « H » alors « C » « réciproques l’un de l’autre, les propriétés représentées «par « H » et par « C3 sont des propriétés   « réciproques »… 

Attention :

Il existe des cas où un énoncé ne possède pas  de réciproque ( vraie).

Par exemple , considérons l’ énoncé suivant :

«  si un entier est divisible par « 10 » , alors il est divisible par « 2 ».

(Expliquez oralement pourquoi cet énoncé est toujours vrai )

L’énoncé réciproque serait :

« si un entier est divisible par « 2 » , alors il est divisible par « 10 » .

Trouvez des exemples d’entiers montrant que ce dernier énoncé est faux …..

Fiche 5 : Exemples de recherche et de rédaction de problèmes.

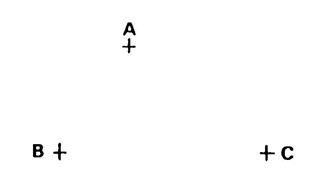
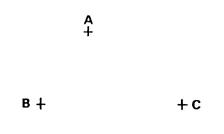
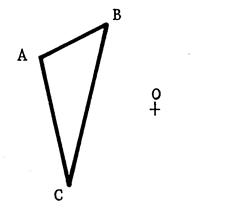
Activité : Exemple 1 :

Ci-contre on vous donne un triangle « ABC » , « M » est le milieu de  |AB] .
La parallèle à  ( BC ) passant par « M » coupe (AC) en « E ».

On appelle « N » le point de ( ME) tel que « E » soit le milieu de [ MN].

Démontrez que ( AN ) et ( MC ) sont parallèles.

Hypothèse :

Conclusion :

Recherche :

( à ne pas écrire dans la rédaction d’un devoir ).

Vous voulez démontrer que deux droites sont parallèles. Vous cherchez alors dans votre cours les théorèmes, propriétés ou définitions qui peuvent vous amener à cette conclusion.

Vous avez à votre disposition la propriété « 3 »(transitivité) , la propriété « 5 »  .

Le théorème n°2 ( droites des milieux) et la définition du parallélogramme.

Ce n’est pas la propriété « 3 » car il faudrait une troisième droite de même direction.

Ce n’est pas  la  propriété « 5 »  car vous n’avez pas de renseignements sur les angles.

Un rapide examen de la figure montre qu’aucune des deux droites  ne peut jouer le rôle de droite des milieux. Il ne reste donc  que la définition du parallélogramme :

Si un quadrilatère est un parallélogramme , alors ses côtés opposés sont  « parallèles » .

La figure te suggère que  « ….. »   est peut être un parallélogramme .

Vous allez le démontrer.

Pour cela vous cherchez parmi les propriétés de la fiche « 3 » celle qui peut convenir.

En fonction des données de l’énoncé ( vous regardez l’hypothèse) et en procédant par élimination vous constatez que la propriété …….( ou la propriété ……) peut convenir à condition de prouver auparavant que « E » est le milieu de ….. ( faites le oralement ).

Démonstration :

Dans le triangle « ABC » , par hypothèse , « M » est le milieu de …|AB] …… et ( ME ) est parallèle à .. ( BC ) donc d’après le théorème n°… , « E » est le milieu de …|AC] ……

D’autre part , par hypothèse , on sait que  « E » est le milieu de …|MN] ……donc , grâce à la propriété n°…     , « AMCN » est un …parallélogramme….  Donc par définition , ses côtés opposés sont ..parallèles….donc  ,  ( AN ) et ( MC ) sont parallèles.

Activité : Exemple 2 :

« ABCD » est un parallélogramme.

         On trace par « A » la parallèle à ( DB) qui coupe  ( BC ) en « E » et ( DC) en « F ».

1°) Démontrez que « A » est le milieu de | FE ] .

2°) Démontrez que « B » est le milieu de |EC]et que « D » est le milieu de | FC] .
 Hypothèse : ………………………………………………..

…………………………………………………….

Dans le cas où le problème comporte plusieurs questions on n’écrit pas la conclusion mais , dans la rédaction, on écrit un titre précisant que l’on veut démontrer.

1°) Démontrons  que « A » est le milieu de | FE ] .

Recherche : la figure vous suggère l’existence de parallélogrammes. Nommez-les : (oralement si possible) .Leurs côtés opposés ont même longueur, alors ………

Démonstration :

Par hypothèse ,  « ABCD » est un parallélogramme, donc , par définition , ( AD) est parallèle   … ( BC).  C'est-à-dire à  ( BE).

Le quadrilatère « AEBD »ayant ses côtés  opposés parallèles est un ..paralélogramme…

Donc , grâce  à la propriété n°… , ses côtés  opposés ont même ……… donc  « AE = DB »…….

De la même façon on prouve que … »FABD » . est un parallélogramme et par suite  «  FA = …DB…. »

Puisque  «  AE = …DB… » et  «  FA = …DB.. »  alors par transitivité de l’égalité :   «  FA …=  ..AE » et puisque « F » , « A » , « E » sont sur la même droite  alors « A » est le milieu de | FE ]  .

Remarque :

Grâce à la démonstration que l’on vient de faire , la conclusion de cette première question peut être considérée par hypothèse pour les questions suivantes.

2°) Démontrez que « B » est le milieu de |EC]et que « D » est le milieu de | FC] .

« ABCD » étant parallélogramme, par définition (AB) est parallèle à …(DC)…..

Dans le triangle « FEC », « A » est le milieu de  | FE ]  .(première question)

Et l’on vient de dire que (AB) est parallèle à (DC), c'est-à-dire à ( FC), alors grâce au théorème n°…  , « B » est  milieu de [ EC ]……

…

On vous de demande de terminer ce travail :     Démontrez de même que « D » est le milieu de  [ FC].

Activité : Exemple 3 

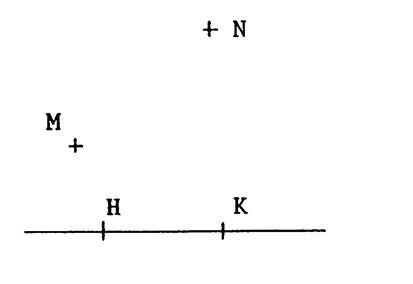
On donne deux points « H » et « K » et « M » et « N » sont deux points quelconques non situés sur  (HK).

Activités :

-        Placez le point « P » tel que « H » soit le milieu de [ MP] ,

-        Placez le point « R » tel que « K » soit le milieu de [ MR] ,  

-        Placez le point « S » tel que « K » soit le milieu de [ NS] , 

-        Placez le point « T » tel que « H » soit le milieu de [ NT] , 

Démontrez que « PRST » est un parallélogramme.

Hypothèse :

Conclusion :

Démonstration :

Dans le triangle « NTS » , par hypothèse , « H » est le milieu de   …….  Et « K »  est …………………………………..

Donc grâce au théorème  ..n°…. , HK =    c'est-à-dire  «  TS = ……. »

A vous de continuer.

Fiche n°6 :  Activités - EXERCICES pouvant être donnés à traiter.

Exercice n°1 :

« ABCD » est un parallélogramme de centre « O ».

« A’ » , « B’ », « C’ » et « D’ » sont les milieux respectifs de  [ MP], [ MP], [ MP],,

Démontrez que  « A’ » , « B’ », « C’ » et « D’ » est un parallélogramme.

Exercice n°2 :

« ABC » est un triangle quelconque.

« D » , « E » , « F » sont les milieux respectifs de [ BC], [ CA], [ AB] ,

Démontrez que [ AD]  et  [ FE] ont même milieu.

Exercice n°3 :

D’après un sujet de BEPC :

« ABC » est un triangle quelconque.

« D » est le milieu de  [AB] , « M » , est le milieu de [ BC], « O » est le milieu de  [ MC] .

Activités :

1°) Démontrez que ( DM ) est parallèle à ( AC )

2°) « F » est le point tel que « O » soit le milieu de [ FD] 

 Démontrez que  « A » , « C » et « F »  sont alignés .

3°) La parallèle à ( AB ) passant par « F » coupe  ( DM) en « E ».

  Démontrez que  « A » , « O » et « E »  sont alignés .

Fiche 7 Exercices sur la symétrie centrale

Info +@ la symétrie……..

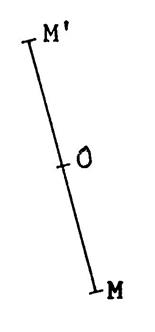
Par définition :

Dire que le point « M » et le point « M’ » sont symétriques par rapport à un point « O » , c’est dire que « O » est le  centre ( milieu) du segment [M M’]

Vous avez vu dans la classe de 5^ème  que , dans toute symétrie centrale , si deux figures sont symétriques, alors elles sont superposables .

En particulier, on rappellera la propriété suivante relative à la droite :

Propriété 17 :

Dans toute symétrie centrale, l’image d’une droite est une ..droite ….la droite et sa symétrique sont ..parallèle »…..

ACTIVITES :

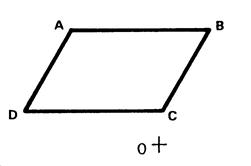
Exercice 1 :

Ci-contre un parallélogramme « ABCD » et un point « O ».

Placez les points « E » , « F » , « G » , « H » qui sont symétriques respectivement de « A » , « B » , « C » , « D » dans la symétrie de centre « O ».

Démontrez que « EFGH » est un parallélogramme.

Exercice 2 :

On donne un cercle de centre « O ».

 [ AB ] est un diamètre.

[  AE ]  et [ BF ]  sont deux cordes  telles que  ( AE ) et ( BF ) soient parallèles .

Démontrez que « E » , « O » , « F » sont alignés.

Exercice 3 :

On donne un parallélogramme « ABCD » et un point « O ».

Dans la symétrie de centre « C », « A » a pour image « E », « B » a pour image « F » ,  « D » a pour image « G », placez les  points.

1°) Nommez tous les segments qui ont pour milieu « C ».

2°) Nommez tous les parallélogrammes ayant pour sommets  quatre des points  « A » , « B » , « C » , « D » ,« E » , « F » , « G ».

(Faîtes une démonstration « oralement ».)

Exercice 4 :

On donne ci-contre un triangle « ABC » et un point « O » quelconque.

Dans la symétrie centrale de centre « O », « B » a pour image « B’ » , « C » a pour image « C’ ».

Tracez par « B’ » la droite « d » parallèle à ( AB).

Tracez par « C’ », la droite « d’ » parallèle à ( AC).

« d » et « d’ » se coupent en « M ».

Démontrez que « M » est le symétrique de « A » par rapport à « O ».

Exercice 5 :

On donne ci-contre un triangle « ABC ». « P » est un point de [BC].

« M » est le milieu de  [AB] . « N » le milieu de [AC].

Soit « E » le symétrique de « P » par rapport à « M » et  « F » le symétrique de « P » par rapport à « N ».

Activité :

Construisez ces deux points.

.

Ensuite :

1°) Déterminez l’image de la droite (BC) dans la symétrie centrale de centre « M », puis dans la symétrie centrale de centre « N ».

Quelle conséquence pouvez-vous en tirer pour les points « E », »A » , « F » ?

2°) Déterminez l’image de la droite ( AP) dans la symétrie centrale de centre « M», puis dans la symétrie centrale de centre « N ».

Quelle conséquence pouvez-vous en tirer pour les droites ( BE) et (CF)

1.    Parallélogramme  ABCD de côtés AB = 35 mm et AD = 45 mm et = 120°

2.   Parallélogramme  ABCD tel que AB = 26 mm et AD = 48 mm et la diagonale BD = 40 mm

3.   Parallélogramme  ABCD de côté AB = 5cm et de diagonales AC = 4 cm et BD = 80 mm

4.   Parallélogramme  ABCD tel que AB = 2,5cm et AD = 5cm et la diagonale AC = 64 mm

5.   Parallélogramme ABCD de côtés AB = 5cm et AD = 4cm et de hauteur  AH = 3cm

6.   Parallélogramme ABCD de côté AB= 30 mm et de hauteurs  AH = 25 mm et AK = 32 mm    ( niveau +++)