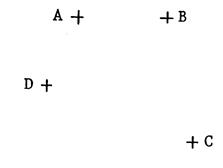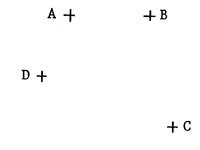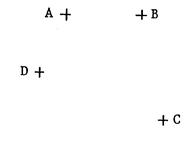|
Niveau V. |
Géométrie : DOSSIER :
les tracés géométriques II / Objectif cours
24b |
|
Classe de 5ème collège -
2ème année / 4 |
|
|
|
|
|
|
|
|
|
ENVIRONNEMENT du dossier:
|
Objectif
précédent |
· Voir le parallélogramme. |
||
|
|
|
|
|
DOSSIER : LE QUADRILATERE
|
|
Fiche
1 : Le
quadrilatère. |
|
|
|
Fiche
2 : Le
parallélogramme. |
|
|
|
Fiche
3 : Le quadrilatère dont les diagonales se coupent en leur milieu. |
|
|
|
Fiche
4 : Quadrilatère dont le point d’intersection des diagonales est centre
de symétrie. |
|
|
|
Fiche
5 : Quadrilatère dont les côtés opposés ont même longueur |
|
|
|
Fiche
6 : Quadrilatère ayant deux côtés parallèles de même longueur. |
|
|
|
Fiche
7 : Constructions de parallélogrammes |
|
|
|
Fiche
8 : Quadrilatère convexe dont les angles sont supplémentaires ou égaux. |
|
|
|
Fiche
9 : Récapitulatif des propriétés des différents quadrilatères |
|
|
|
Activités :
Fiche 10 construction d’un carré |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Devoir évaluation |
|
||||||
|
|
Fiche
1 : Le quadrilatère. |
|
|
||
|
|
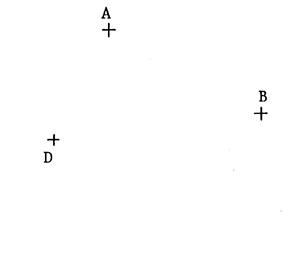
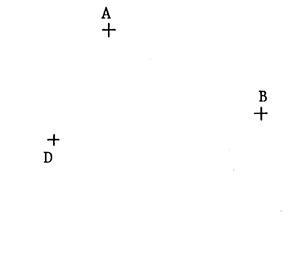
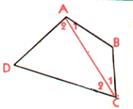
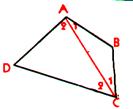
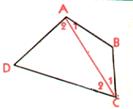
· « A », « B », « C »,
« D » sont quatre points distincts . Ci-dessous
on vous a représenté 3 dessins identiques
comportant ces quatre points dans la même position. Dans les
trois cas , joignez par des segments les points dans
l’ordre indiqué. ( n’oubliez pas de joindre le
dernier point au premier…) |
|
|||
|
|
Figure 1 : « ABDC » |
Figure 2 : « ABCD » |
Figure
3 : « ACBD » |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vous
constatez que vous n’obtenez pas la même figure dans les trois cas. : |
|
|||
|
|
La figure
« 2 » : représente un « quadrilatère
convexe ». La figure
« 1 » et « 3 » : représentent chacune un « quadrilatère croisé ».
|
|
|||
|
|
|
|
|||
|
|
· Sans changer la disposition des points , mais en
changeant l’ ordre, pensez-vous qu’il soit possible d’obtenir d’autre
figures ? ……………………… |
|
|||
|
|
· L’ordre des points étant donné, il n’y a qu’une possibilité de
figure. Par contre, la figure,
on pour la désigner, on opérera
toujours de la façon suivante : le premier point nommé est celui
qui se trouve le plus à gauche et le plus haut , ainsi dans l’exemple
ci-dessus , le point le plus haut à
gauche est « A ». ensuite on listera les autres points l’un après
l’autre, dans le sens des aiguilles d’une montre… Ici le parallélogramme est
« ABCD ». |
|
|||
|
|
|
|
|
|
|
Fiche
2 : Le
parallélogramme. |
|
|
|
|
On entend souvent : Si un quadrilatère a
ses côtés opposés parallèles deux à
deux c’est un parallélogramme. |
|
|
|
|
A )
Définition. |
|
|
|
|
Si nous
énonçons que : Un quadrilatère est un parallélogramme, cela
signifie que « ses côtés opposés sont parallèles ». |
|
|
|
|
Cet énoncé
peut s’appeler une définition. Elle nous
donne deux informations : 1°) Dans
l’ensemble des quadrilatères ceux qui
ont leurs côtés opposés parallèles sont appelés
« parallélogrammes ». 2°) Si on
sait qu’un quadrilatère est un parallélogramme, alors on peut affirmer que ses
côtés opposés sont parallèles. · Le parallélogramme possède d’autres propriétés : Nous
allons vous les rappeler ci-dessous ( vous les avez rencontrées dans les fiches précédentes ) Auparavant , remarquez que tout
parallélogramme est nécessairement « convexe »
et qu’on le nomme comme il l’est dit dans la fiche 1 . |
|
|
|
|
|
|
|
|
|
B )
Propriétés L5) |
|
|
|
|
Dans tout
parallélogramme : |
|
|
|
|
-
Les diagonales se
coupent en leur ……………….…….. |
|
|
|
-
Les côtés opposés ont
même ………………..…… |
|||
|
-
Le centre est centre
de …………………..….pour ce parallélogramme |
|||
|
-
Les angles opposés
sont ………………………… |
|||
|
|
-
Les angles consécutifs
sont ………………..…… |
|
|
|
|
|
|
|
|
|
C ) Posons la question suivante : |
|
|
|
|
Si un
quadrilatère possède une de ces propriétés , est-il
un parallélogramme ? C’est ce
que nous allons étudier dans les fiches suivantes. |
|
|
|
|
|
|
||||
|
|
Fiche
3 : Le quadrilatère dont les diagonales se coupent en leur milieu. |
|
|
|||
|
|
|
|
||||
|
|
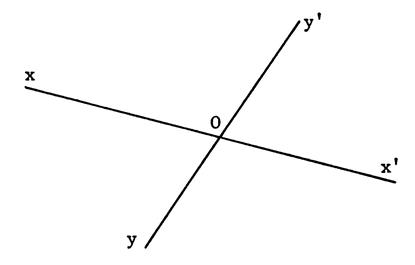
Ci-contre
on vous donnes deux droites « xx’ » et « yy’ »
qui se coupent en « O ». A l’aide
de votre compas , que vous piquez en « O », placez sur
« xx’ » deux points « A » et « C » tels que
« O » soit le milieu de [ AC ] . Changez
l’écartement de votre compas et placez sur « yy’ »
deux points « B » et « D » tels que « O » soit
le milieu de [ BD]. Tracez les
côtés du quadrilatère
« ABCD ». Apparemment
« ABCD » est-il un parallélogramme ?............... |
|
|
|||
|
|
C’est ce
que nous allons prouver par un raisonnement. |
|
||||
|
|
|
|
||||
|
|
Considérons
la symétrie de centre « O ». Puisque
« O » est le milieu de [ AC ] , alors
« A » a pour symétrique …. « …….. ».. Puisque
« O » est le milieu de [ BD ] , alors
« B » a pour symétrique …. « ……… ». Donc la
droite ( AB )
a pour symétrique la droite ………………. Or vous
savez que dans toute symétrie centrale , si deux
droites sont symétriques alors elles sont ……………………… Donc ( AB ) et ( CD )
sont ……………….….. Ayant ses
côtés opposés parallèles ,alors par définition ,
« ABCD » est un ………………………….. |
|
||||
|
|
A retenir : Tout quadrilatère dont les diagonales se coupent
en leur milieu est un ……………………….. ….. |
|
||||
|
|
|
|
||||
|
|
Activité n°…….. |
|
||||
|
|
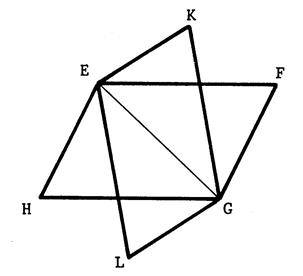
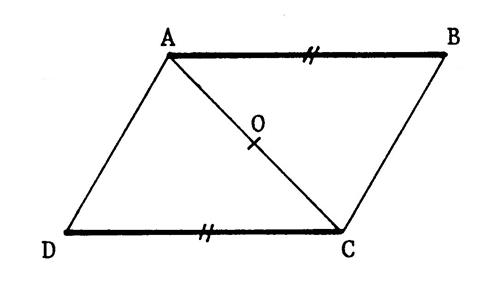
« EFGH »
et « EKGL » sont deux parallélogramme qui ont la même diagonale [ E G ]. Nous
allons prouver que « KFLH » est un parallélogramme. ______________________________________________ Appelons
« M » le milieu de [ EG ]. Puisque
« EFGH » est un parallélogramme alors « M » est aussi le
milieu de ……………. ……… Puisque
« EKGL » est un parallélogramme alors « M » est aussi le
milieu de ………………….……. Donc ………… ……….et …………….... ont
le même milieu. Puisque « HKFL » a ses diagonales
qui se coupent en leur milieu , alors «
HKFL » est un ……………………..… |
|
|
|||
|
|
|
|
||||
|
|
Fiche
4 : Quadrilatère dont le point d’intersection des diagonales est centre
de symétrie. |
|
|
|||
|
|
|
|
||||
|
|
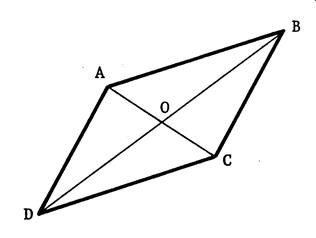
Ci-contre , on vous donne un quadrilatère
« A BCD» dont les diagonales
se coupent en « O »et tel que « O » soit le centre de
symétrie. Prouvons
que « ABCD » est un « ………………………… ». |
|
|
|||
|
|
Réponse : Puisque
« O » est centre de symétrie, alors « O » est le milieu
de [ AC ] et
« O » est milieu de [ BD]. Onc les
diagonales du quadrilatère « ABCD » se coupent …………………………. Donc
« ABCD » est un ………………..……….. |
|
||||
|
|
|
|
||||
|
|
A retenir : Tout
quadrilatère ayant pour centre de symétrie le point d’intersection de ses
diagonales est un …………………………. |
|
||||
|
|
|
|
|||
|
|
Fiche
5 : Quadrilatère dont les côtés opposés ont même longueur |
|
|
||
|
|
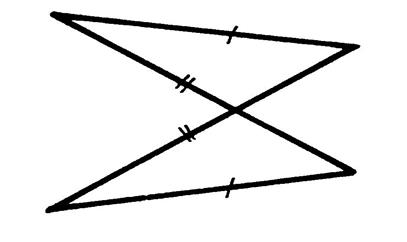
Il est
possible de prouver par un raisonnement que : Tout
quadrilatère ayant ses côtés opposés de même longueur est : |
|
|||
|
|
soit un quadrilatère croisé. |
soit un parallélogramme. |
|
||
|
|
|
|
|
||
|
|
|
|
|||
|
|
A retenir : Tout
quadrilatère « convexe » ayant ses côtés opposés de même longueur
est un …………………………….. |
|
|||
|
|
|
|
|||
|
|
Activité
n°…. |
|
|||
|
|
En
utilisant la règle et le compas , ( ne prenez pas
d’équerre pour tracer les parallèles), vous allez construire les
parallélogrammes
« EFGH » et « ABCD ». |
|
|||
|
|
Parallélogramme « EFGH ». |
Parallélogramme « ABCD ». |
|
||
|
On donne le côté [ H G ] . HE = 28 mm et |
On donne la diagonale [ DB ] Et DA = 25 mm ; BA =
45 mm |
||||
|
|
|
||||
|
|
|
||||
|
|
Activité n°2 .. |
|
|||
|
|
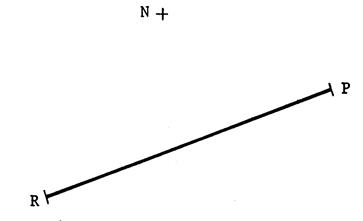
Toujours
en utilisant le compas (sans utiliser d’équerre pour tracer les parallèles ) , Vous allez
construire le parallélogramme « MNPR »
dont on donne le point « N » et le côté [ RP
] |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
Activité n°3 .. |
|
|||
|
|
En vous
inspirant de la construction précédente ,
(c'est-à-dire en utilisant le compas mais pas l’équerre ) , par le point
« O » , vous allez tracer la parallèle à la droite « d ». |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
Fiche
6 : Quadrilatère ayant deux côtés parallèles de même longueur. |
|
|
||
|
|
Par abus , on dit
« côtés parallèles »
au lieu de « côtés dont les supports sont parallèles ». |
|
|||
|
|
« ABCD »
est un quadrilatère convexe tel que ( AB ) et ( DC )
sont parallèles et AB = DC . Nous
allons prouver par un raisonnement que « ABCD » est un …………………………………….… |
|
|
||
|
|
|
|
|||
|
|
Appelons
« O » le milieu de [ AC ].[ Considérons
la symétrie de centre « O ». Puisque
« O » est le milieu de [ AC ] , alors
« A » et « C » sont symétriques. La droite
( CD ) étant parallèle à la droite ( A
B ) et « ABCD » étant convexe,
les demi- droites [ AB ) et
[ CD ) sont symétriques. Et comme
AB = CD ,
alors « B » a pour symétrique « ……….. ». Donc
« O » est le milieu de ………………………………. Le quadrilatère « ABCD » a donc ses diagonales qui se coupent en
leur milieu. Alors,
grâce à ce que l’on a établi à la fiche 3 . On peut
dire que « ABCD » est un …………………………... |
|
|||
|
|
A retenir . Tout quadrilatère
convexe ayant deux côtés parallèles et de même longueur est un ………………………………… |
|
|||
|
|
|
|
|||
|
|
Activité
n°…… |
|
|||
|
|
« EFGH » est un parallélogramme. Placez sur
[ EF ] le
point « M » tel que Placez sur
[ HG ] le point « N » tel que Prouvez
par un raisonnement que ( EN ) et ( MG ) sont
parallèles. |
|
|
||
|
|
Indication : Que
pouvez-vous dire du quadrilatère « EMGN » ? …………………………………….…… Prouvez –le…………… |
|
|||
|
|
|
|
|||
|
|
|
|
|||||
|
|
Fiche
7 : Constructions de parallélogrammes |
|
|
||||
|
|
|
|
|||||
|
|
Dans les 3
cas ci-dessous ,
on donne 3 points « A » ,
« B » , « D ». A vous de
déterminer le pont « C » pour que « ABCD » soit un
parallélogramme. Et cela de
trois façons différentes ( suivant la propriété
utilisée ). Laissez
les constructions apparentes et tracez les côtés du parallélogramme. |
|
|||||
|
|
|
|
|||||
|
|
1°) Les diagonales se coupent en
leur milieu. Tracez – les . Utilisez la règle graduée. |
2°) Côtés opposés parallèles . Utilisez le compas. |
3°) Côtés opposés de même longueur. Utilisez le compas. |
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|||||
|
|
|
|
|||||
|
|
Fiche
8 : Quadrilatère convexe dont les angles sont supplémentaires ou égaux. |
|
|
||||
|
|
|
|
|||||
|
|
Situation A : |
|
|||||
|
|
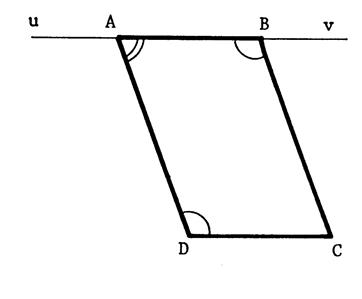
Les
données sont : Ci-contre
un quadrilatère convexe « ABCD » dont les anges consécutifs sont
supplémentaires deux à deux. Nous
allons prouver par un raisonnement que « ABCD » est un …………………………………………… |
|
|
||||
|
|
|
|
|||||
|
|
Désignons
par « uv » le support du côté [ AB ] . Donc
Or, les
angles Relativement
aux droites ( A D ) et ( B C ) et
à la sécante ( A B ) , Donc,
d’après ce qui a été étudié dans la leçon n°…. fiche ……. On peut
dire que les droites ( A D ) et ( B C ) sont
……………………. On prouverait de même que (
A B ) et ( D C ) sont ……………………. « ABCD » est , par
définition , un …………………………………………….. |
|
|||||
|
|
Situation B : |
|
|||||
|
|
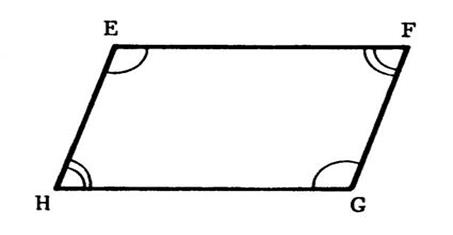
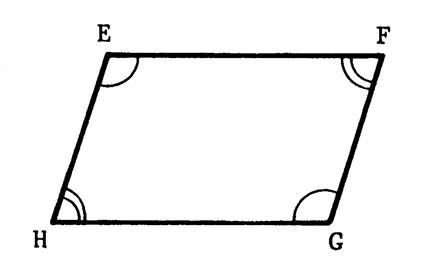
Ci-contre
un quadrilatère convexe « EFGH » dont les angles opposés sont égaux
deux à deux . Nous
allons montrer et prouver par un raisonnement que « EFGH » est un ………………………………. |
|
|
||||
|
|
Les
angles Les angles
« EFGH »
étant un quadrilatère convexe , la somme de ses
angles est égale à …. ……………..…… On peut
alors écrire : « x + y + x + y = 360° » C'est-à-dire : « 2 x + 2 y = 360° » Ou
encore : «
2 ( x + y ) = 360° » Donc : « x + y = 360° Puisque
« x + y = 180° » alors Il en est
de même pour Donc,
d’après ce qui a été prouvé plus haut , on peut
affirmer que « EFGH » est un
…………………………..……. |
|
|||||
|
|
A retenir : Tout quadrilatère convexe dont les
angles consécutifs sont supplémentaires ou dont les angles opposés sont
égaux deux à deux est un
parallélogramme. |
|
|||||
|
|
|
|
|||||
|
|
Activité
n° :………. |
|
|||||
|
|
|
|
|||||
|
|
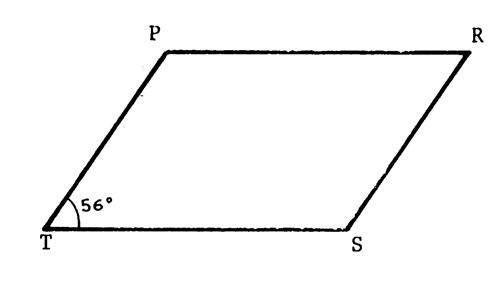
« PRST »
est un parallélogramme tel que Tracez la
bissectrice de Tracez la
bissectrice de Complétez :
Calculez :
Puis
prouvez que « PNSM » est un parallélogramme. |
|
|
||||
|
|
|
|
|||||
|
|
|
|
||||||
|
|
Fiche
9 : Récapitulatif des propriétés des différents quadrilatères. |
|
|
|||||
|
|
|
|
||||||
|
|
Quadrilatères |
Parallélogramme |
Rectangle
|
Losange
|
Carré
|
|
||
|
|
||||||||
|
Deux
paires de côtés parallèles. |
|
|
|
|
||||
|
Côtés
consécutifs perpendiculaires. |
|
|
|
|
||||
|
Côtés
opposés de même longueur. |
|
|
|
|
||||
|
Côtés
consécutifs de même longueur. |
|
|
|
|
||||
|
Diagonales
se coupant en leur milieu. |
|
|
|
|
||||
|
Diagonales
de même longueur. |
|
|
|
|
||||
|
Diagonales
perpendiculaires. |
|
|
|
|
||||
|
Angles
consécutifs supplémentaires. |
|
|
|
|
||||
|
Angles
opposés égaux . |
|
|
|
|
||||
|
|
|
|
||||||
|
|
Ce tableau
une fois rempli faire apparaître des faits déjà connus : · Le rectangle possède toutes les propriétés du parallélogramme. ( il en possède
d’autres en plus.). Ce qui est normal car tout rectangle est d’abord un ………………………….. · De même tout losange est d’abord un …………………………….…………. · Et tout carré est d’abord un ..parallélogramme……………. · Vous constatez aussi que le carré possède à la fois les propriétés du ………………..
et du ……………………….…… Ce qui est
normal car tout carré est à la fois un
« ……………….. » et un « ………………………….. »………. |
|
||||||
|
|
|
|
||||||
|
|
Activités :
Fiche 10 construction d’un carré. |
|
|
|||||
|
|
|
|
||||||
|
|
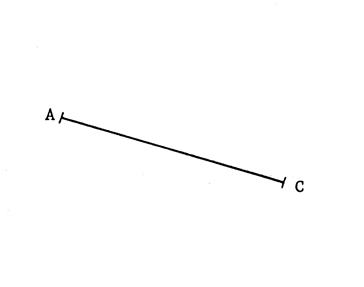
Construisez
le carré « ABCD » dont on donne la diagonale [ AC
] Laissez
les constructions apparentes. Oral :
justifiez que le quadrilatère obtenu est un bien un carré. |
|
|
|||||
|
|
|
|
||||||
CONTROLE :
1.
Donnez la
définition d'un quadrilatère
2.
Donner le
nom de 5 quadrilatères « particuliers »
Série 1 :
1) Tracer un
quadrilatère convexe.
2 ) Tracer un
quadrilatère non convexe.
3°) Construire
à la règle et au compas la médiatrice ( D) d'un segment AB de
Placer sur la médiatrice deux points C et D situés de part et d'autre de F tels que F
soit le milieu de [ C D ] . Que
représente la droite ( AB) pour le segment [ CD] . Quelle est la nature du quadrilatère
ACBD ?
Série 2 :
EXERCICES DE CONSTRUCTION : Tracer les figures suivantes ………
Interdisciplinarité :
en ébénisterie.
Formule calcul du nombre de queue d’aronde à répartir sur la
largeur d’une planche . La queue d’aronde est un trapèze .
![]()
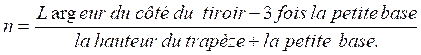 ou
ou 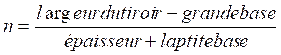
la petite base =
épaisseur divisée par 5
Les
parallélogrammes
|
1°) Parallélogramme ABCD de côtés AB = |
|
|
2°)
Parallélogramme ABCD tel que AB = |
|
|
3°)
Parallélogramme ABCD de côté AB = 5cm
et de diagonales AC = |
|
|
4°)
Parallélogramme ABCD tel que AB =
2,5cm et AD = 5cm et la diagonale AC = |
|
|
5°)
Parallélogramme ABCD de côtés AB = 5cm et AD = 4cm et de hauteur AH = 3cm |
|
|
6°)
Parallélogramme ABCD de côté AB= |
|
|
1°) Rectangle ABCD tel que AB = 55mm et AD = |
|
|
2°) Rectangle ABCD de diagonale |
|
|
3°) En +++ : Rectangle ABCD de diagonale |
|
|
4°) En plus : rectangle ABCD de longueur
triple de la largeur et de périmètre |
|
|
1°)Losange ABCD tel que
AB = |
|
|
2°) Losange ABCD de diagonales AC = |
|
|
3°) Losange
ABCD de diagonale BD = |
|
|
4°) En
plus : losange d’aire A = 6cm2 et de diagonale AC = |
|
|
1°) Carré de côté AB = |
|
|
2°) Carré de diagonale AC = |
|
|
4°) En plus : carré de périmètre p = |
|
|
5°)En plus : carré d’aire A = 1225 mm2 |
|
|
Exercices
d’identification : Soit le
parallélogramme ABCD et « O » le point d’intersection des
diagonales |
|
Consignes : mettre une croix pour les figures
concernées ; justifier.
|
Propriétés
ou caractères |
trapèze |
Trapèze
isocèle |
Trapèze
rectangle |
parallélogramme |
rectangle |
Losange
|
Carré
|
justification |
AB //
DC
|
|
|
|
|
|
|
|
|
|
AO
=OC= OD = OB |
|
|
|
|
|
|
|
|
|
AB =
BC=CD=DA |
|
|
|
|
|
|
|
|
|
AB//DC
et |
|
|
|
|
|
|
|
|
|
BC //
AD et |
|
|
|
|
|
|
|
|
|
AB = CD et AD = BC |
|
|
|
|
|
|
|
|
|
Rectangle
et AB = BC |
|
|
|
|
|
|
|
|
|
Parallélogramme
tel que AC ^ BD |
|
|
|
|
|
|
|
|
|
Propriétés
ou caractères
|
trapèze |
Trapèze isocèle |
Trapèze rectangle |
parallélogramme |
rectangle |
Losange |
Carré |
justification |
|
AD //
BC et |
|
|
|
|
|
|
|
|
|
AB //CD Et AD // BC |
|
|
|
|
|
|
|
|
|
Losange
tel que |
|
|
|
|
|
|
|
|
|
AB //DC et AB =DC=BC |
|
|
|
|
|
|
|
|
|
Médiatrice
de AB et médiatrice de DC confondues |
|
|
|
|
|
|
|
|
|
AB // CD et AB = CD |
|
|
|
|
|
|
|
|
|
[AC]
et [BD ] médiatrices l’une de l’autre |
|
|
|
|
|
|
|
|
|
AD //
BC et AB = CD |
|
|
|
|
|
|
|
|
|
m(A,C) = m ( B,D)= 0 |
|
|
|
|
|
|
|
|
|
Propriétés
ou caractères
|
trapèze |
Trapèze
isocèle |
Trapèze
rectangle |
parallélogramme |
rectangle |
Losange
|
Carré
|
justification |
|
Losange
tel que AC = BD |
|
|
|
|
|
|
|
|
|
m(A,C) et m (B,D) = 0 et AC
= BD |
|
|
|
|
|
|
|
|