fiche pédagogique sur la découverte des propriétés du parallélogramme.


	Vous savez que l’on appelle « parallélogramme » tout quadrilatère dont les opposés sont ….parallèles…….. Dessinez ci –dessous un parallélogramme dont on donne les supports de deux côtés parallèles. ( évitez de faire un rectangle ) On appellera « ABCD » ce parallélogramme. ( placez les points sur la figure ) .

	1^ère Propriété .
	Tracez les diagonales [ A C ] et [ DB] . Appelez « O » leur point d’intersection. En utilisant votre compas que vous piquez en « O », (ou en mesurant ), - Comparez les longueurs OA et OC , vous constatez que ………………………………………………. - Comparez les longueurs OB et OD , vous constatez que ………………………………………………. C'est-à-dire que « O » est à la fois ……………………………….de [ A C ] et de [ DB] Ce que vous venez de constater , il est possible de le prouver par un raisonnement. (Ce raisonnement est un peu compliqué, on ne le fera pas dans cette fiche…) Vous admettrez alors la propriété suivante qui est vraie pour tout parallélogramme.
	A retenir : Dans tout parallélogramme , les diagonales se coupent en leur milieu. Ce point est appelé le « centre » du parallélogramme.

	2^ème Propriété.
	Comparez les longueurs AB et DC, vous constatez que ………………………………………… Comparez les longueurs AD et BC , vous constatez que ……………………………………….. Vous venez de faire les mesures . Or vous savez que les mesures sont toujours imprécises. Pour affirmer que les égalités que vous venez d’écrire sont toujours vraies, il faut le prouver par le raisonnement. Voici un tel raisonnement que l’on appelle une démonstration…

	D’après la propriété énoncée précédemment , propriété qui est vraie car on peut faire un raisonnement qui l’affirme ), on peut dire que « O » est le ….milieu….. de [ AC ] et « O » est le milieu de [ DB ] . Donc, dans la symétrie centrale de centre « O » , « A » a pour symétrique le point … »C »…. Et « B » a pour symétrique le point … »D »…. Le segment [ AB ] a pour symétrique le segment …[ CD] ……. Or vous savez que le symétrique est un segment de même …longueur…………………. Donc les longueurs AB et CD sont ……de même mesure ……… On prouverait de même que les longueurs …AD.. et ………BC……………sont ……………identiques……………. On peut donc énoncer la propriété suivante.
	A retenir : Dans un parallélogramme , les côtés opposés ont même ….mesure……

	Activité n°…….
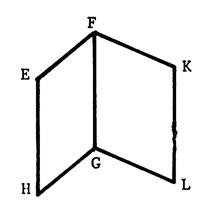
	Ci-contre : on vous a dessiné deux parallélogramme « EFGH » et « FGLK » qui ont été commun. Démontrez ( c'est-à-dire prouvez par un raisonnement) que « EH = KL »
	30/01/2014

TRAVAUX AUTO FORMATIFS

CONTROLE :

(6^ème) 1 ) Donner la définition d’un parallélogramme :

(5^ème) 2 ) Citer les trois principales propriétés d’un parallélogramme.

EVALUATION

1°) construire un parallélogramme , sachant que deux côtés consécutifs mesurent respectivement 3 cm et 5 cm et que l’angle compris entre ces deux côtés mesure 54°.

Calculer les autres angles de ce parallélogramme .

2°) construire sans rapporteur un parallélogramme , sachant que ses deux diagonales mesurent respectivement 7 cm et 5 cm et forment entre elles un angle de 120°.

3°)Construire un parallélogramme dont les côtés mesurent respectivement 5,5 cm et 3,5 cm et la hauteur 2 cm.

4°) Construire sans rapporteur un parallélogramme , sachant que le côtés AB mesure 6 cm , la diagonale AC 8 cm et que l’angle BAC est égal à 30°.

5° ) Construire un parallélogramme ABCD , sachant que le côté AB mesure 3 cm , le côté BC 5 cm et la diagonale AC 7 cm.

Autres :

1. Parallélogramme ABCD de côtés AB = 35 mm et AD = 45 mm et = 120°
2. Parallélogramme ABCD tel que AB = 26 mm et AD = 48 mm et la diagonale BD = 40 mm
3. Parallélogramme ABCD de côté AB = 5cm et de diagonales AC = 4 cm et BD = 80 mm
4. Parallélogramme ABCD tel que AB = 2,5cm et AD = 5cm et la diagonale AC = 64 mm
5. Parallélogramme ABCD de côtés AB = 5cm et AD = 4cm et de hauteur AH = 3cm
6. Parallélogramme ABCD de côté AB= 30 mm et de hauteurs AH = 25 mm et AK = 32 mm ( niveau +++)

INTERDISCIPLINARITE