Index Warmé Raymond - warmaths
Niveau V et niveau IV A RETENIR	RESUME sur :

LES QUADRILATERES :

La définition ; la description, les propriétés et l’identification des quadrilatères.

Devoir : Contrôle

Devoir évaluation ; tracé

TRAPEZES @ :

Il y a 3 Différentes sortes de trapèze :

En RESUME :

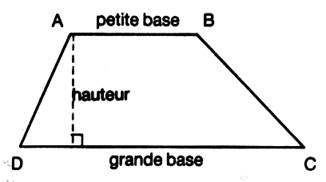
1°)Trapèze quelconque
Définition description : - Quadrilatère convexe ayant deux côtés parallèles . [DC] // [AB] - [DC] et [AB] sont les bases. DC > AB  [AB] est la plus petite base et [DC] est la plus grande base.
Propriétés: les angles ayant pour sommets les extrémités d’un des côtés non parallèles sont supplémentaires . + = 180° et + = 180° Identification : Quadrilatère convexe ayant deux côtés parallèles . [DC] // [AB]

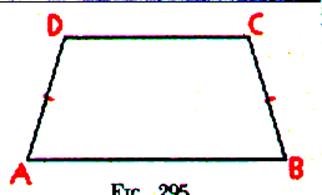
2°) Trapèze isocèle
Définition : C’est un trapèze dont les cotés non parallèles sont isométriques. (1)AD = BC Propriétés: -Propriétés du trapèze quelconque -les angles à la base sont égaux = et = (2) - les médiatrices des bases sont confondues ( 3) - l’axe de symétrie : médiatrice des bases l’identification se fait avec (1) ou (2) ou (3)

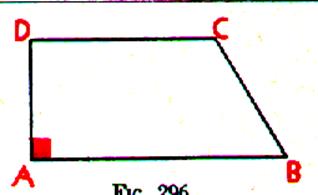
3°)Trapèze rectangle DCBA
Description :Trapèze ayant un angle droit : = 1 droit Propriétés : - propriétés du trapèze quelconque - si = 90° alors = 90° Identification à partir de : Trapèze ayant un angle droit.

II )LE PARALLELOGRAMME

En RESUME :

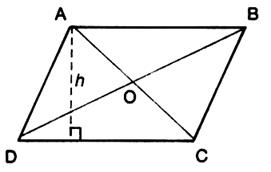
Définition : Le parallélogramme est un quadrilatère convexe dont les côtés opposés sont parallèles deux à deux . [DA ] // [ BC ] et [ AB] // [ CD ] (1) Propriétés : -les côtés opposés sont deux à deux isométriques DA = CB et AB = DC (2) - les angles opposés sont égaux deux à deux = et = ( 3) - deux angles consécutifs sont supplémentaires (somme = 180°) - les diagonales [ AC] et [ DB] se coupent en leur milieu (voir + : la symétrie centrale) (4) - (5 ) deux côtés sont isométriques et parallèles

Identification : quadrilatère ayant la propriété (1) ou (2) ou ( 3) ou ( 4) ou (5)

III ) LE RECTANGLE

En RESUME :

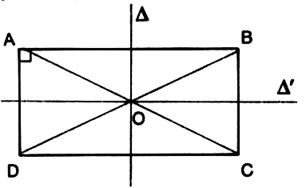
Définition : Parallélogramme ayant un angle droit . ( 1) AB > BC alors [ BC ] est la largeur et [ AB] est la longueur	Propriétés : du rectangle : Possède les propriétés du parallélogramme et : - les quatre angles sont droits = = = - les diagonales [ AC] et [ DB] sont isométriques AC = BD (2) - 2 axes de symétrie : médiatrices des longueurs et des largeurs - 1 centre de symétrie : le point de concours des diagonales se coupent en leur milieu (voir + : la symétrie centrale)
Identification : parallélogramme ayant la propriété (1) ou (2)

IV ) LE LOSANGE

En RESUME :

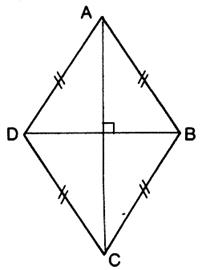
Définition : Parallélogramme ayant deux côtés consécutifs isométriques (1) Propriétés :du losange Possède les propriétés du parallélogramme et : - les quatre côtés sont isométriques DA = AB = BC = CD - les diagonales [ AC] et [ DB] sont perpendiculaires (AC) ^ (BD) (2) (elles sont médiatrices l’une de l’autre et bissectrices des angles du losange) - 2 axes de symétrie : supports des diagonales - 1 centre de symétrie : points de concours des diagonales (voir + : la symétrie centrale)

Identification : parallélogramme ayant la propriété (1) ou (2)

V ) LE CARRE

En RESUME :

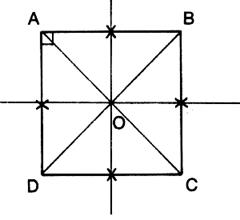
Définitions : Rectangle ayant deux côtés consécutifs isométriques (1) Ou Losange ayant un angle droit (2) AB = BC = CD= DB = a = = = = 90° le carré est un polygone régulier . Propriétés : - possède les propriétés du rectangle et du losange  - 4 axes de symétrie : les 2 du rectangle et les 2 du losange ) - 1 centre de symétrie : point de concours des axes de symétrie (voir + : la symétrie centrale) - (la mesure des diagonales = d = a ) -

Identification : utilisation de (1) ou (2)