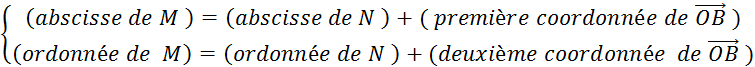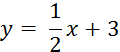|
|
TITRE :
Fiche sur LES
EQUATIONS DE DROITES de
la forme : y = mx + p dans un repère |
|
|
|
Classe
de 3ème |
|
|
|
|
|
|
|
|
|
|
|
Pré requis:
|
|
|
|
|
ENVIRONNEMENT du dossier:
AVANT :
|
APRES : 1°) Les droites croissante ; décroissante,.. |
Complément d’Info :
|
Travaux ; devoirs
|
|
Corrigé
|
|||
|
|
Contrôle |
évaluation |
|||
|
Interdisciplinarités : (matière concernée) |
||||||||
|
F |
H |
Géo. |
Vie quotidienne et vie familiale |
Autres : |
Sciences et technique |
Physique Chimie Electricité |
Statistique. |
|
|
|
|
|
|||||||
|
|
Fiche:
|
|
|
||||||
|
|
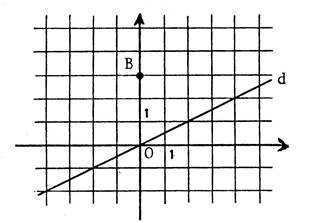
Le
plan est muni d’un repère d’origine « O ». « d »
est la droite d’équation « « B »
est le point de coordonnées ( 0 ; 3 ). Complétez : Considérons
la translation de vecteur Vous
savez que l’image d’une droite par une
translation est une droite. |
|
|
||||||
|
|
La
droite et son image sont parallèles
. On
vous demande de tracer la droite « Soit
« M » un point quelconque de « On
peut considérer que « M » est l’image par la translation d’un point
« N » de « d ». Placez « M » et « N » sur la figure. |
|
|||||||
|
|
D’après
ce que l’on a vu dans le cours … « vecteur et translation » , on peut
dire : |
|
|||||||
|
|
|
|
|||||||
|
|
Puisque ( Puisque
« N » est situé sur « d » qui a pour équation « On
a alors |
|
|||||||
|
|
|
|
|||||||
|
|
Inversement :
un point dont les coordonnées ( x ; y ) vérifient la relation Considérons
un point R ( x ;
y ) tel que |
|
|
||||||
|
|
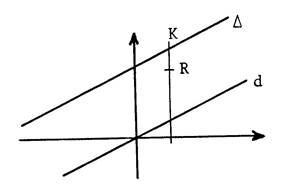
Traçons
par « R » la parallèle à l’axe des ordonnées. Elle
coupe « « R »
et « K » ont alors la même abscisse : « Puisque
« K » est sur « C’est
la même que celle de « R ». « R »
et « K » ayant les mêmes coordonnées sont donc confondus donc « R » est sur « |
|
|||||||
|
|
En
définitive : Tout
point dont les coordonnées ( x ; y ) vérifient |
|
|||||||
|
|
|
|
Est
appelée : Equation de la droite « |
|
|||||
|
|
Cette
relation est vérifiée par les coordonnées de chacun des points de la droite
« |
|
|||||||
|
|
Conséquence : Que
peut-on dire des points de coordonnées
( x ; y ) tels que Ils
ne sont pas sur la droite d’équation ………………. |
|
|||||||
|
|
|
|
|||||||
|
|
Vocabulaire : Pour
la droite « d » , d’équation |
|
|||||||
|
|
|
|
|||||||
|
|
Pour
la droite « Le nombre « 3 » qui est
l’ordonnée du point « B » , intersection
de « |
|
|||||||
|
|
|
|
|||||||
|
|
Remarque : « En
choisissant une autre parallèle à « d », on aurait trouvé le même
coefficient directeur. |
|
|||||||
|
|
|
|
|||||||
|
|
|
|
|||||||
|
|
Activité
1 : |
|
|||||||
|
|
Un
point de « Un
point de « |
|
|||||||
|
|
|
|
|||||||
|
|
Activité
2 : |
|
|||||||
|
|
Parmi
les points suivants , déterminez par le calcul ceux
qui sont situés sur « |
|
|||||||
|
|
|
|
|
|
|
|
|
||
|
H ( -6 ; 0) |
C ( 0,2 ; 3,1 ) |
D ( 4 ; - 5 ) |
J ( |
R ( |
S = ( |
||||
|
|
Vous
avez trouvé les points : ……………………………………………………….. |
|
|||||||
|
|
|
|
|||||||
|
|
Droites
particulières. |
|
|||||||
|
|
|
|
|||||||
|
|
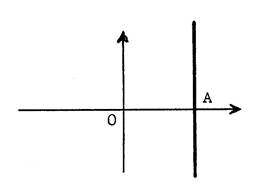
Considérons
la droite passant par : A ( 3 ; 0 ) et
parallèle à l’axe des ordonnées. Tous
les points de cette droite ont même abscisse : ..3 ….et tous les points qui sont sur cette droite L’équation
de cette droite est :
« |
|
|
||||||
|
|
· D’une
manière générale, toute droite parallèle à l’axe des ordonnées a une équation
de la forme : «
|
|
|||||||
|
|
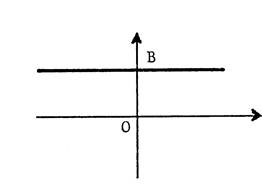
Considérons
la droite passant par « B ( 0 ; 2
) »et parallèles à l’axe des abscisses . Tous
les points de cette droite ont même ordonnée : …2….
Et tous les points qui ont cette ordonnée sont sur cette droite. L’équation
de cette droite est :
« |
|
|
||||||
|
|
· D’une
manière générale, toute droite parallèle à l’axe des abscisses a une équation de la forme : « |
|
|||||||
|
|
Cas général : |
|
|||||||
|
|
Le plan est muni d’un repère d’origine « O ». Etant donné une droite non parallèle à l’axe des ordonnées
, existe-il une relation liant les coordonnées de chacun des points de cette
droite ? |
|
|||||||
|
|
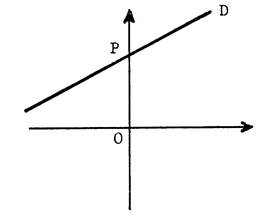
Voir
ci-contre : Désignons
par « D » une telle droite. Elle
coupe l’axe des ordonnées en un point « P ». Appelons
« p » l’ordonnée de « P », complétez : « P ( . 0.. ; p….) » IL
existe une droite passant par « O » et parallèle à « D ». Appelons
« d » cette droite , tracez –la. |
|
|
||||||
|
|
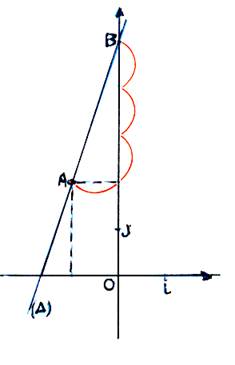
Il
existe un nombre « En
considérant la translation de vecteur Relation
dans laquelle : « m »
représente le même nombre que dans « On
démontrerait aussi que les points de « D » sont les seuls à
vérifier cette relation. |
|
|||||||
|
|
D’où
le théorème : |
|
|||||||
|
|
Théorème : Dans
le plan muni d’un repère , toute droite non
parallèle à l’axe des ordonnées a une équation de la forme : |
|
|||||||
|
|
|
|
|||||||
|
|
la
forme : |
|
|||||||
|
|
|
|
|||||||
|
|
Vocabulaire : Pour
toute droite d’équation |
|
|||||||
|
|
|
|
|||||||
|
|
Remarques : On a vu que les droites parallèles à l’axe des abscisses
ont pour équation une relation de la forme « Cette
équation est de la forme Les
droites passant par l’origine ( à part l’axe des
ordonnées) ont une équation de la forme
Il
n’y a que les droites parallèles à l’axe des ordonnées qui n’ont pas
d’équation de la forme : |
|
|||||||
|
|
|
|
|||||||
|
|
· La plan muni
d’un repère , « |
|
|||||||
|
|
Il
est possible de démontrer que la réponse est « oui » . ( on ne le fera
pas à ce niveau
) |
|
|||||||
|
|
Soit
le théorème suivant : |
|
|||||||
|
|
Théorème : Le
plan étant muni d’un repère ,
« m » et « p » étant des nombres quelconques , l’ensemble
des points du plan dont les
coordonnées ( x ; y ) vérifient |
|
|||||||
|
|
|
|
|||||||
|
|
|
|
|||||||
|
|
|
|
|||||||
|
|
|
|
|||||||
|
|
|
|
|||||||
|
|
|
|
|||||||
|
|
|
|
|||||||
TRAVAUX AUTO FORMATIFS.
- Donner la procédure permettant de tracer une droite à partir d’un
coefficient directeur et un point appartenant à la droite .
Tracer une droite : dont on connaît m = 3 ; et A ( -1 ; +2 )
corrigé CONTROLE:
Donner la procédure permettant de tracer une droite à partir d’un
coefficient directeur et un point appartenant à la droite .
|
Procédure : Equation de la forme « y = m x +p » |
|
On connaît « m » et A ( xA; y A)
|
|
On place le point A |
|
On place un point B dont les
coordonnées sont (xA
+ 1) ; (y A + m ) |
|
On trace la droite ( D) qui
passe par les deux points |
corrigé
EVALUATION:
Tracer une droite : dont on connaît m = 3 ; et A ( -1 ; +2 )
|
Soit
m = 3 ; et A ( -1 ; +2 ) |
|
Placer A ; coordonnées
x A= -1 ; y A=+2 |
|
On place un point B dont les
coordonnées sont : ( xA +
1) ; (y A + m ) soit (-1 + 1) ; (2 + 3
) ; soit les coordonnées de B ( 0 ; 5) |
|
|