Pré requis:

Résoudre une équation du premier degré à 2 inconnues ( solutions : des couples de points)
Droites et repérage
Les repère cartésiens

ENVIRONNEMENT du dossier:

Index

AVANT : Représentation d’une droite. Repérage d’un point  dans un plan.

COURS

APRES : 1°) recherche de l'équation d'une droite à partir de deux coupes de points. 1°)Droites positions dans un repère 2°)Le coefficient directeur 3°)  Les droites croissante ; décroissante,.. 4°)le parallélisme et la perpendicularité 5°) tracer d'une droite ou courbe dans un repère.

Complément d’Info : Liste des objectifs de cours Fonction affine (présentation)   Résumé

Dossier : géométrie : LES DROITES DANS UN REPERE :

A) Construction d’une droite avec deux points dont on connaît les coordonnées.

B) Construction d’une droite dont on connaît l’équation.

 

Travaux ; devoirs				Corrigé
TEST	Contrôle	évaluation		Contrôle	évaluation

 

Interdisciplinarités :   (matière concernée)
F	H	Géo.	Vie quotidienne et vie familiale	Autres :	Sciences et technique	Physique Chimie Electricité	Statistique.

 

 

 

COURS

Introduction :

                 Une droite dans un repère est la représentation graphique de la fonction  d'équation  y = a x + b;

 

Cette fonction, du premier degré, est représentée graphiquement par une droite parallèle  à la droite d'équation y = a x  et coupant l'axe O y  au point d'ordonnée "b" .

 

Cette fonction y = ax + b  , appelée "fonction affine" est appelée "fonction linéaire" lorsque "b" = 0 . pour s' écrire  y = a x .

 

Cette équation , représentant la fonction affine ,  y = ax + b  est aussi appelée : équation de la droite .

 

Le coefficient "a" détermine  la pente de la droite et s'appelle "coefficient directeur" .et le nombre "b" est    "l'ordonnée à l'origine" .

Le point d'intersection de la droite  y = a x + b avec l'axe O x  a pour ordonnée y = 0 . Son abscisse  vérifie la relation a x + b = 0 et est égale à x =

    

Important :    Dans tout ce qui suit le plan est muni d’un repère  ( O,I, J) ou (( O , ,  ) )

 

A)  Construction d’une droite avec deux points dont on connaît les coordonnées.

 

Procédure :	Application : y
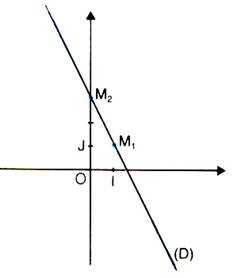
1°) on donne  deux points M 1  et M 2   et leurs  coordonnées  respectives. Tel que :     M 1  (x 1 ; y 1 )  et M 2 (x 2 ; y 2 )	M 1  (1 ; 1 )  et M 2 (0 ; 3 )     x 1 = 1 et x 2  = 0
2°) on place le  point M 1	Pour M 1 ( 1 ; 1 ) on trace les droites  x 1 = 1 et y 1 =   1
3°) on place le points  M 2	Pour M 2  ( 0 ; 3  ) On trace les droites x 2  = 0  et y 2   =  3
4°)       on trace la droite  passant par M 1 M 2.	INFO plus sur le repérage d’un point dans un repère cartésien. !

 

 

B) Construction d’une droite dont on connaît l’équation.

Rappel :  Equation de  la droite

             La droite (D) est formée de tous les points   dont les coordonnées « ( x , y ) » sont liées par la relation mathématique :  y = a x + b .

 

Exemple : y = 2x - 1

 

Activité 1 : recopier et compléter le tableau suivant :

Abscisse « x » d’un point de (D)	x	-3	0	1			2	-2	4
Ordonnée « y » du même point	y				3	-2

 

 

Activité 2 : prendre une feuille de papier millimétré , graduer deux droites  perpendiculaires , prendre pour unité un cm .

Placer  ces  10  points sur le repère ; avec une règle constater que les points tracés sont alignés .

 

On obtient le tracé ci-contre en joignant tous ces points . Vérification : choisir d’autres valeurs de « x » et trouver « y » en utilisant la relation « 2x-1 », et constater qu’à chaque calcul le nouveau point se trouve sur la droite .

 

Activité 3 :

Graduez le repère ci dessus.

Choisissez 5 points sur (D) différents de ceux choisis précédemment ;

Exemples :  -2,5 ; - 1,5 ; + 1,5 ; + 3,5 ;+4

Point :		A	B	C	E	F
Abscisse « x » d’un point de (D)
Ordonnée « y »du même point .

 

Activité 4 :

Soit l’équation  y = 2x+1

Prendre les 5 valeurs choisies précédemment ;

Et compléter le tableau ;

 

Point :		A	B	C	E	F
Abscisse « x » d’un point de (D)
Ordonnée « y »du même point . par calcul y = 2x+1

 

Comparer les coordonnées de chaque point ; si une erreur existe , elle doit être liée à la qualité et la précision des tracés .

 

Vous constatez qu’un point de la droite ( D) a des coordonnées  ( x ; y ) telles que  y = 2x – 1

 

Propriété :

Soit « m » et « p » deux nombres.

            Tous les points du plan dont les coordonnées ( x ; y ) sont liées par la relation  y = m x + p  sont situés sur une même droite  ( D ) .

La relation y = m x + p est appelée «  équation de la droite ( D) parce que seules les coordonnées des points de ( D ) la vérifient .

 

Procédure concernant la construction d’une droite dont on connaît une équation :

 

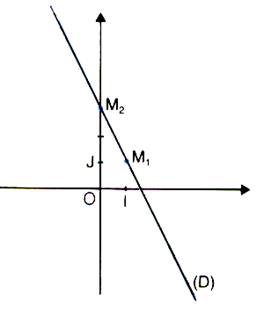
Equation théorique : y = m x + p	Application : y = -2 x + 3
1°) on donne ou choisi deux valeurs à « x » ;  x 1  et x 2	x 1 = 1 et x 2  = 0
2°)on calcule les valeurs correspondantes y 1  et y 2	y 1 = -2 (1) + 3   =  1   et y 2   =  - 2 ( 0 ) + 3 = 3
3°) on place les points M 1  et M 2	M 1 (1 ; 1 )  et M 2  ( 0 ; 3  )
4°)       on trace la droite  passant par M 1 M 2

 

Travaux auto formatifs.

 

CONTROLE:

1°)  Donner la forme  d’une équation de droite.

2° ) Donner la procédure  permettant de tracer une droite à partir d’une équation.

 

 

EVALUATION:

SERIE 1 :

1.         Dans un repère orthonormal, on considère les courbes  suivantes :

 

(C₁ ) : y = -2x +1 ; (C₂ ) : y = x² + 3 y² = 5 ; (C₃ ) : y = 7x ; (C₄ ) : y = x y + 3 x = 0 ; (C₅ ) : y = 5 ; (C₇) : y = 3x + 6 y - 10 = 0

 

Parmi ces courbes, quelles sont celles qui sont les représentantes d’une droite ?

 

 

2 . Dans un repère orthonormal , soit la droite (D) : y = 6 1,5 x + 2,5

 

 Dire si les points suivants appartiennent à la droite (D) :

                                   A ( 2 ; - 5) ; B ( 0,2,5 ) ; C ( -1 ; -1 ) et F (-6 ; 5 )

 

3 . Dans un repère orthonormal, on considère les droites :

 

D₁ :   y = 2x + 5 ;  D₂ :   y =  - 3 x + 8 ; D₃ :   y = x - 7 ; D₄ :   y =  - x + 1

 

Déterminer le coefficient directeur de chacune de ces droites

 

4. Dans un repère orthonormal , soit la droite ( D) :  y = -0,5 x + 2

 

a) déterminer les ordonnées des points A ; B ; C et D d’abscisses respectives : 1 ; 4 ; -7 et -2

 

b) Déterminer les abscisses des points E ; F ;G et H d’ordonnées respectives : 1 ; 4 ; -7 et -2

 

5 . Dans un repère orthonormal , tracer les droites :

 

(D ₁ )  de coefficient directeur  « -1 » et passant par le point de coordonnées ( 0 ; 2 ) ;

(D ₂ )  de coefficient directeur  « 0,5 » et passant par le point de coordonnées ( 0 ; -1 ) 

(D ₃ )  de coefficient directeur  « -1,5  » et passant par le point de coordonnées ( 1 ; -3 ) 

(D ₄ )  de coefficient directeur  « 2 » et passant par le point de coordonnées ( -1 ; 1 ) 

 

6. . Dans un repère orthonormal, tracer  les droites :

 

D₁ :   y = 2x + 5 ;  D₂ :   y =  - 3 x + 8 ; D₃ :   y = x - 7 ;  D₄ :   y =  - x + 1

 

7. Dans un repère orthonormal , déterminer une équation de la droite ( D) passant par le point A ( 0 ; 5 ) et  B ( -2 ; 3 )

 

SERIE 2 :

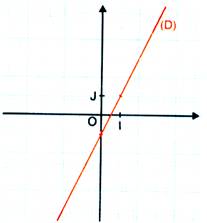
1°) dans un repère cartésien tracé une droite d’équation «  y = - 2x + 3 »

 

Séries :

Première série de tracés :

Tracer les quatre droites  (D₁) ; (D₂) ; (D₃) ; (D₄) suivantes données par leur équation de la forme : y = mx + p

 

(D1)	(D2)	(D3)	(D4)
y = 2 x + 3	y = -3x +3	y = x+3	y = x +3

 

Que  constate-t-on ? ; quelles sont les coordonnées du point « commun » ?

 

Deuxième  série de tracés :

Tracer les trois droites  (D₁) ; (D₂) ; (D₃) ; suivantes données par leur équation de la forme : y = mx + p

 

(D1)	(D2)	(D3)
y = 3 x + 2	y = x + 2	y = x+2

 

Imaginons que ces droites représentent le profil d’une route  en montagne.

Classer dans l’ordre croissant  de celle qui monte le moins à celle qui monte le plus .

Que est la relation ( valeur ) qui lie la « pente » et le tracé

 

troisième  série de tracés :

 

Tracer les trois droites  (D₁) ; (D₂) ; (D₃) ; suivantes données par leur équation de la forme : y = mx + p

 

 

(D1)	(D2)	(D3)
y = -3 x + 2	y = - x + 2	y = -x+2

Imaginons que ces droites représentent le profil d’une route  en montagne.

Classer dans l’ordre de celle qui descend  le moins à celle qui monte le plus .

 

Quelle  est la relation ( valeur  ) qui lie la « pente » et le tracé ?.