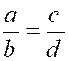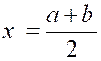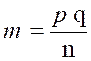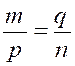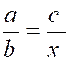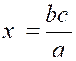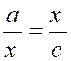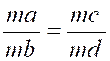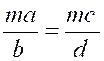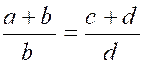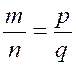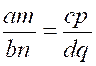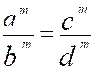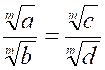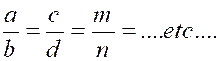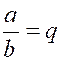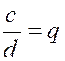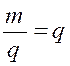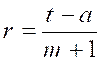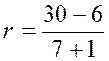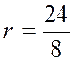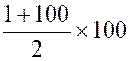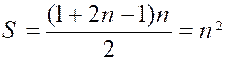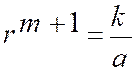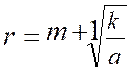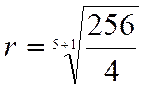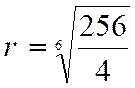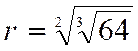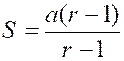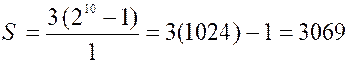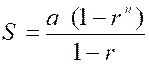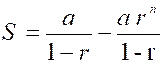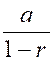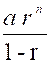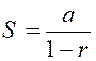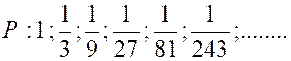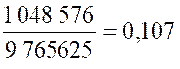|
|
|
|
Multiplication
d’une fraction par un nombre |
ENVIRONNEMENT du dossier:
|
Les grandeurs proportionnelles (présentation) |
1°) Sommaire : sur les grandeurs
proportionnelles 2°) Les suites ou progressions.. |
DOSSIER :
Généralités sur
LES RAPPORTS , LES PROPORTIONS et LES
PROGRESSIONS.
|
Chapitres : |
|
|
|
|
||||||
|
1) |
Des (
2) rapports .
(définitions) |
|
|
|
|
|||||
|
|
·
« rapport
par différence » ou rapport arithmétique. |
|
|
|
|
|||||
|
|
· « rapport par
quotient » ou rapport géométrique. |
|
|
|
|
|||||
|
2) |
|
|
|
|
||||||
|
|
|
|
|
|
||||||
|
|
|
|
||||||||
|
3 ) |
|
|
|
|||||||
|
|
|
|
||||||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||
|
|
||||||||||
|
|
|
Travaux auto formatifs |
|
|
|
|
||||
|
TEST |
COURS |
|
Corrigé Contrôle |
Corrigé évaluation |
||||||
COURS
|
1) |
|
|||
|
|
En général, on appelle rapport le résultat de la comparaison de deux
quantités; mais deux quantités mathématiques,
a et b, ne peuvent être comparées que de deux manières : 1° pour savoir de combien l'une surpasse l'autre : 2° combien de fois l'une contient
l'autre. Dans le premier cas, on obtient le rapport
au moyen d'une soustraction, et on le nomme pour cela rapport par différence ou rapport
arithmétique. Dans le second cas, le rapport est le
quotient d'une division, et on l'appelle rapport par
quotient ou rapport
géométrique. Ainsi, a — b exprime le rapport arithmétique des quantités a et b; tandis que Dans les deux cas, les quantités que l'on
compare, a et b, se nomment les termes du rapport. Les deux termes d'un rapport doivent
représenter des quantités de la même espèce ou être pris dans un sens abstrait, sans
quoi le rapport n'aurait pas de signification, |
|
||
|
2) |
|
|||
|
|
On donne .le nom de proportion à
l'expression de deux rapports égaux. La proportion est arithmétique ou géométrique, selon
que les rapports que l'on compare sont par
différence ou par quotient. La proportion arithmétique s'appelle
aussi équi différence, tandis que le mot « proportion »
tout seul s'entend de la proportion
géométrique. On indique la proportion
arithmétique comme il suit : a . b : c . d, ou bien a
— b = c — d La proportion
géométrique s'écrit ainsi : a : b :: c : d,
ou (a : b ):
(c : d) ou mieux encore Dans le premier cas, on
prononce « a est à b » comme « c est à d »,
et dans le second, « a divisé par b »
égale « c divisé par d », ou plus brièvement, « a sur b
égale c sur d » Dans toute proportion, le
premier terme a et le dernier d se nomment les extrêmes,
tandis que les intermédiaires b
et c s'appellent les moyens. Une proportion dans
laquelle les deux termes moyens sont égaux, se nomme proportion continue; ainsi (a - m) : (m - d)
et (p : n): (n : q)sont des proportions continues. Dans ce cas, la quantité m est une moyenne proportionnelle arithmétique
entre a et d,
tandis que n est moyenne proportionnelle géométrique entre les extrêmes p et q . |
|
||
|
|
Propriétés des équi- différences. |
|
||
|
|
Principe
fondamental. Dans toute proportion arithmétique,
la somme des extrêmes est égale à la somme
des moyens. Ce principe découle de la définition; en effet, poser a . b
: c . d c'est exprimer que a — b = c — d, ou bien, en transposant, que a + d = b + c. Ce théorème donne le moyen de retrouver
un des quatre
termes d'une équi-différence dont les trois
autres sont
donnés : soit, par exemple, a . b : c . x ; puisqu'on doit avoir a + x = b + c, on aura x = b
+ c — a. Si la proposition était continue et qu'on eût a. x : x. b, ,
on aurait 2x = a + b, ou bien
|
|||
|
|
||||
|
|
· Propriété fondamentale. Dans toute
proportion géométrique, le produit des extrêmes est égal au produit des
moyens. Soient les quatre quantités proportionnelles a, b,
c, d qui donnent les rapports égaux Réciproquement, Quand le
produit de deux facteurs est égal au
produit de deux autres, ces quatre facteurs forment
une proportion. En effet, soit l'égalité m x n= p x q ; (
que l’on peut écrire : m n = p q ) si l'on divise d'abord les deux membres par n et ensuite
par p, on aura
On voit donc que quatre quantités forment
une proportion dans deux circonstances distinctes, selon que, prises deux à deux, elles donnent des quotients ou des
produits égaux ; or, pour fixer les idées,
on dit que deux quantités a et b
sont directement proportionnelles à deux autres c et d, quand
on a et que deux
quantités m et n sont inversement ou
réciproquement proportionnelles à deux autres p
et q, quand on a mn =
p q. ·
La propriété
fondamentale d'une proportion géométrique
fournit le moyen de retrouver un quatrième terme
dans une proportion dont les trois autres sont connus ; en effet, les deux rapports égaux alors
x se nomme une moyenne proportionnelle géométrique entre les deux quantités a
et c. Une
moyenne géométrique entre deux quantités est donc la racine carrée du produit de ces deux
quantités. ·
La propriété fondamentale et sa
réciproque servent à démontrer toutes les propriétés des proportions En effet, la proportion
ce qui prouve que dans toute proportion on peut, sans la détruire, 1° Multiplier les quatre termes par un même nombre 2° Multiplier les deux numérateurs par un
même nombre ; 3° Augmenter chaque numérateur de son
dénominateur. Ce que nous disons pour la multiplication
et l'addition est vrai aussi pour la division et la soustraction. ·
Quand on multiplie
deux proportions, terme à terme, les produits sont en proportion, En effet, les deux égalités
donne
évidemment cette nouvelle égalité
il en serait de même si l'on divisait, terme à terme,
le; deux proportions données. Il en découle de là deux autres principes : ·
Dans toute
proportion, on peut élever les quatre termes
à une même puissance, ou bien en extraire une racine du même degré, sans détruire la proportion. Ainsi : Dans une suite de
rapports égaux, ta somme des
numérateurs et la somme des dénominateurs ont entre elles un rapport égal aux rapports donnés. Supposons qu’on ait Représentons ce rapport commun par « q » et
posons :
ce qui
donne a = b q ; c = d q ; m = n q ; ajoutons ensuite, membre à membre,
et mettons q en facteur commun pour avoir
l'égalité a + c + m = (b + d + n)q ; celle-ci donne à son tour : |
|
||
|
|
||||
|
|
On donne le nom de progression
à une suite indéfinie de termes tels
que le rapport qui existe entre deux termes consécutifs est constamment le même dans toute la série. *µCe rapport constant
s'appelle la raison de la progression, et celle-ci est arithmétique ou géométrique, selon que le rapport est une
différence ou un quotient ; ainsi, si l'on écrit S 1 : 4 . 7 . 10 . 13 , 16 . 19
. etc..., ; on forme une progression
arithmétique dont la raison est
3; tandis que si l'on écrivait S2 : 2 : 4 : 8 : 16 : 32 : 64.
etc... ; on aurait une
progression géométrique dont 2 est la raison. Les progressions sont
dites croissantes ou décroissantes.,
selon que les termes vont en augmentant ou en diminuant. A
) Propriétés des progressions arithmétiques
ou par différence. ·
principe fondamental. Dans toute progression arithmétique croissante, un terme
d'un rang quelconque est
égal au premier terme, augmenté d'autant de fois la raison ( r ) qu'il y a de termes avant celui que l'on
cherche. Soit en général la progression
croissante : a ;
b ; c ; e ;
f ; g ……….. dont nous représenterons la raison
par r. D'après la définition même, il est évident qu'on aura b
= a + r ; c
= b + r = a + 2 r ; e = c
+ r = a + 3 r ; etc..................................... c'est-à-dire que la
progression pourra être écrite ainsi : Prog. a ; a + r ; a + 2 r ; a + 3 r ; a + 4 r ....... ; ce qui démontre le principe énoncé.
En conséquence, si l'on désigne par t un terme quelconque et par n le
rang qu'il occupe, ce
terme en aura alors n — 1 avant lui, et sa valeur sera exprimée par la
formule formule
[a] : t = a + (n — 1 )r Comme application, si
l'on demandait le 15e terme de la progression par différence écrite ci-dessus (*), dont le premier terme est 4 et la
raison 3, on aurait T = 4 + 14 X 3 == 46. D'après ce principe, on
peut résoudre le problème suivant : problème Ier. Insérer entre deux termes donnés un nombre quelconque de moyens arithmétiques ou différentiels, c'est-à-dire former une progression par différence dont le premier terme et le
dernier sont connus. Supposons qu'on veuille
insérer m moyens différentiels entre a et t ; alors le
dernier terme t en aura m +1 avant lui, et la formule [a] donnera t = a + (m+1 )r ; et comme la seule
inconnue ici est la raison r , on tirera sa valeur qui est formule [ b ]
; Proposons-nous, par
exemple, d'insérer sept moyens différentiels entre les deux nombres 6 et 30 ;
la formule [ b
] donnera pour la raison inconnue.
et la progression demandée
sera : 6 ; 9 ; 12 ; 15 ; 18 ; 21 ; 24 ; 27 ; 30. Remarque. Si l'on insérait un même nombre de moyens différentiels entre tous les
termes consécutifs d'une progression donnée, on formerait ainsi une seule et
même progression, parce que la formule [ b
] donnerait la même raison pour toutes les insertions. théorème. Dans toute progression arithmétique, les termes à égale distance des extrêmes font une somme
constante, Soit la progression
arithmétique croissante On sait que la raison
étant représentée par r , on a « b = a + r » ; « c = a + 2 r » ; «d = a + 2 r » ; etc…........ Si l'on renverse les
termes pour former la progression décroissante la raison n'aura pas changé, et l'on
aura k =
l — r ; h =
l — 2r ;…….. , etc. … En conséquence,
ces deux progressions, ajoutées
terme à terme, donneront a + l = b + k = c + h = etc. ……. pboblème 2 . Trouver la somme des termes d'une progression par différence. Appelons « S » la somme des termes de la progression :
nous aurons évidemment S = a + b + c + .... ..........+ h + k + l, S = l + k + h + .........+ c + b + a ; en
ajoutant « terme à terme »
et en désignant par « n » le nombre des
termes, Aussi : ( a + l )
= ( b + k) = ( c +
h) = ……= (h + c) = (k + b) =( l
+ a ) tel que En additionnant S + S
= ( a + l ) + ( b + k)
+ ( c + h) + ……+ (h + c) + (k + b) +( l +
a ) et en
désignant par « n » le nombre des termes, nous obtenons 2 S
= (a + l)n,
d'où par conséquent : La somme des terme d'une progression par différence quelconque est égale à la demi somme des deux termes extrêmes, multipliée par le nombre des
termes de cette progression. |
|
||
|
|
problème 3
Trouver la somme des cent premiers
nombres entiers depuis 1 jusqu'à 100. |
|
||
|
|
Nous avons ici
une progression arithmétique dont la raison
est 1; ainsi la formule [c] deviendra S = |
|
||
|
|
problème 4 . Exprimer la somme « S » des « n »
premiers nombres impairs. |
|
||
|
|
Les nombres impairs font une progression
par différence dont la raison est 2 ;- on aura donc a = 1 ; r
= 2 ; l = l + 2 ( n –
1) = 2n — 1, et la formule [c] donnera ainsi la somme des n
premiers nombres impairs est i carré de n. Minutes [a] et [c} résolvent toutes
les questions relatives aux progressions par différence. (Voir v
n<» 281 à 257.) |
|
||
|
|
|
|
||
|
|
|
|
||
|
|
B ) Propriétés des progressions géométriques ou « par quotient » , |
|
||
|
|
Principe
Fondamentale : Dans toute progression
géométrique croissante, un terme d'un rang
quelconque est égal au premier multiplié par la raison élevée à
la puissance marquée par le nombre des termes qu'il y a
avant celui que l'on cherche. Soit la progression par
quotient : : Prog. = D’après la définition,
si l'on représente la raison par « r » pourra écrire ainsi cette progression
et si l’on désigne par n
le rang du terme l , qui
alors aura n— 1 termes avant
lui, on aura : l = a
q n-1 ; formule : [d], Cette
formule démontre le principe énoncé. Proposons-nous,
pour exemple, de calculer le 7 ième terme de la
progression Prog : = La formule [d] donnera l = 4 x 26
= 286. Ce principe nous servira à résoudre le problème
suivant .. problème 1er. Insérer entre deux termes
donnés un nombre quelconque de moyens géométriques ou
proportionnels Supposons qu'on veuille insérer m moyens
géométriques entre a et
k : alors le dernier terme k en aura « m+1 » avant lui., et la formule [d] deviendra : k = a r m+1 Et comme l’inconnue , ici , est la raison « r » , on
aura : c'est-à-dire qu'on
obtiendra la raison cherchée en divisant le dernier terme par le premier, et en
extrayant du quotient la racine
dont le degré est marqué par le nombre plus un des moyens à insérer. Cette raison sera rarement entière; mais dans le cas
où elle est moindre que l'unité, la progression est décroissante. Prenons un exemple dans la
progression numérique précédente, et proposons-nous d'insérer 5 moyens géométriques entre les deux nombres 4 et 256; la règle
et la formule [e] donneront
pour la raison cherchée :
et nous aurons la progression : Remarque. Si l'on insérait entre les termes
consécutifs d'une progression
donnée un même nombre de moyens géométriques, on formerait une seule et même progression, parce
que la raison serait la même partout. problème II. Trouver
la somme des termes d'une
progression géométrique. Soit la progression par quotient qu'on écrit aussi de cette manière : en nommant S la somme cherchée, on aura S
= Si l’on
multiplie tous les termes de cette égalité par la raison « r » , on obtient : S
r
= Et en retranchant la première somme
“S” de celle ci , on aura : S
r – S = a rn – a
; ou S(
r – 1 ) = a
( rn – 1 ); D’ où enfin la formule
[f] : Application : Soit, par exemple, à calculer la
somme des 10 premiers termes de la progression S =
3 ;6 ;12 ; 24 ;…………….. Nous aurons Les formules [ d
] ;[ e ] et [ f ] résolvent toutes les questions relatives
aux progressions par quotient. |
|
||
|
|
Cliquez Ici pour exercices :…… |
|
||
|
|
Quand la progression géométriques
est décroissante , c'est-à-dire quand la raison
« r » est une fraction , il y a lieu de modifier la formule
[ f ] en changeant les
signes des termes , parce que le dénominateur « r -1 »devient
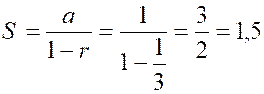
négatif par la supposition de « r < 1 » . Cette formule est donc, dans ce cas , [ g ] ou bien Sous cette forme on voit que la
somme « S » se compose de deux parties : La première Enfin, à l’infini on a
rigoureusement Exemple : Ainsi, dans la progression
indéfinie : On aura : |
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
|
|
TRAVAUX AUTO FORMATIFS :
Revoir
le cours chapitre par chapitre……….
1°) Questions
relatives aux progressions
arithmétiques ( dites aussi : par
différence) : Citer les deux formules à reconnaître et utiliser
pour résoudre les exercices sur les questions relatives aux progressions
arithmétiques ( dites aussi : par différence) :
Réponses : : formule [a] : t = a + (n
— 1 )r ; et 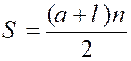 ; formule [ c ]
; formule [ c ]
2°) Questions
relatives aux progressions géométriques ( dites aussi : par quotient) :
Citer les trois formules à reconnaître et utiliser pour résoudre les exercices
sur les questions relatives aux progressions géométriques ( dites aussi :
par quotient) :
Réponses : d ; e ; f dans
le cours
I ) Exercices sur les questions relatives aux progressions arithmétiques
( dites aussi : par différence)
EXERCICES ET PROBLEMES
sur ibs progressions,
1°) Que! est le 12* terme d'une
progression arithmétique dont la raison est 4 et le premier terme 2 ?
2° ) Quel serait le 12éme terme si la raison était ![]() ?
?
3°) On demande d'insérer 5 moyens
différentiels entre 2 et 20
4° ) Etant donnée la progression
![]() 3 ; 10 ; 17 ;
24.. ,
3 ; 10 ; 17 ;
24.. ,
on se propose d'insérer 4 moyens différentiels entre chaque ternie . quelle
sera la nouvelle progression ?
5 °) . Faire h somme des
termes de la progression
![]() 2 ; 5 ; 8 ;...... 29.
2 ; 5 ; 8 ;...... 29.
6°)
Calculer :
a) la somme des mille
premiers nombres naturels ; b ) la somme
des cent premiers nombres impairs 1,3, 5, 7, etc. .
7°) . Quel est le 18ème nombre pair dans la série des nombres entiers ?
II) Exercices sur les questions relatives aux progressions géométriques
( dites aussi : par quotient )
1°) On demande le 7ème terme d'une progression par quotient
dont le
premier terme est 5 et la raison 3.
2°) Quel serait ce 7ème terme si la raison était un tiers
3°) Insérer 2 moyens géométriques
entre 3 et 375.
4°) Quelle est la raison de la progression
géométrique décroissante : P = 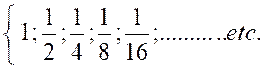
et quelle est la somme des termes de cette série
décroissante et indéfinie ?
5 °) On propose
d'insérer 8 moyens géométriques entre les nombres 3 et 4.
6°).
Étant donnée la progression
P= ![]() : 4 : 16 : 64,
: 4 : 16 : 64,
On
propose d'en former une autre, en insérant 11 moyens géométriques entre les termes successifs de la proposée,
7°) On
demande la somme des termes de la progression
P= ![]() 2 ; 4 ; 8 ;……… ; 256.
2 ; 4 ; 8 ;……… ; 256.
8°) . Calculer la somme des 12 premiers termes de la progression décroissante
P = 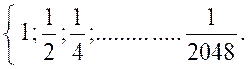
III) Situations problèmes :
1°) Un ouvrier place à
la caisse d'épargne une première économie de 6 € ., et
chaque semaine il y dépose 2 €. de plus; quelle somme aura-t-il placée à
la fin de l'année?
(Rép. 2964 €.)
2°).On donne à un mineur, pour creuser un
puits de 15 mètres de profondeur, 2 €. 75 c. pour le premier mètre, et une augmentation de 0 €. 60 c. pour chaque mètre suivant. Combien coûtera
a) le 15ème mètre, b ) le travail, entier ?
(Rép. Te 15ème mètre 11 €. 15, le tout 104 €, 35.)
3°) On a vendu un cheval, à condition
qu'on le payerait 1 centime d’euro pour le premier clou de ses
fers, 2 centimes pour le second clou, 4 centimes pour le troisième, et ainsi de
suite en doublant
jusqu'au trente-deuxième
clou; quel est le prix du cheval ?
(Rép. 42949672 € . 95.)
4°). Un jardinier est chargé de fumer une allée de 40 arbres distants de 6 mètres chacun ; le tas de fumier est
éloigné de 15 mètres du premier
arbre ; on demande le chemin que ce jardinier aura à parcourir pour déposer un
panier d'engrais au pied de chaque arbre.
(Rép. 2 X
5280 = 10560 m.)
5°) On sait que dans une machine pneumatique la course du
piston correspond à une capacité qui est le quart de celle du réservoir ; on demande la quantité d'air qui restera
dans le réservoir
après 10 coups de piston.
Solution. Les
quantités d'air enlevées à chaque coup de piston, comme les quantités
restantes, sont en progression géométrique décroissante, ayant
même raison, laquelle est ![]() , mais dont le premier terme est
, mais dont le premier terme est ![]() pour l'air restant et
pour l'air restant et ![]() pour
l'air enlevé.
pour
l'air enlevé.