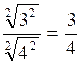Pré requis:

Racine carrée nomenclature :

ENVIRONNEMENT du dossier:

Index

Objectif précédent

2°) Puissance N^ième

3°) Puissances des nombres relatifs.

Objectif suivant

Tableau synoptique à revoir 82

Info complémentaire

DOSSIER: Niveau 4 : Les radicaux (calculs)

	1°) Cours : « Le nombre incommensurable », rappels
	2°) Travaux auto formatifs .

TEST Ou		COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité	Corrigé Contrôle	Corrigé évaluation

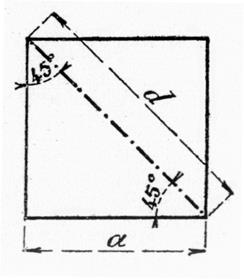
La racine de certain nombre est dit : nombre « incommensurable » Exemple : Si l’on mesure la diagonale « d » d’un carré en prenant comme unité de mesure le côté « a », on ne trouve aucune partie de l’unité « a » contenue un nombre exact de fois dans « d » , on dit qu’il n’y a pas de « commune » mesure entre « d » et « a » , le résultat de la mesure est un nombre incommensurable . Dans le cas de la figure ce nombre est Dans la pratique des opérations , on se contente d’une mesure approchée de la grandeur donnée et l’approximation varie avec la nature de la mesure à effectuer.

Cas Général : la racine n^ième

COURS

Rappels de cours :

« A » étant un réel positif , il existe deux réels « a » et « a’ » dont le carré est égal à « A » . Ils sont opposés. Celui des deux qui est positif se note « » et l’autre est «- » . « A » est appelé « le radicande »
Attention , il ne faut pas confondre :
· La condition « A 0 » indispensable pour que « A » soit un radicande. · La convention selon laquelle désigne un nombre positif.

« A » étant un réel quelconque, il existe un réel unique « a » tel que son cube soit égal à « A ». On note « » . Les écritures « a3 » et « a = » ont exactement la même signification.
Vous savez que les réels « r » tels que « r² » ne sont pas des décimaux ; certes , on peut en donner des valeurs décimales approchées, par exemple : « 1,414 » : mais les calculs ne seraient alors approximatifs ; on trouverait pour « ( 1,41)⁴ » un peu moins de « 3,952 » alors « r⁴ » est égal à « 2² » , c'est-à-dire « 4 ».
On préfère souvent conduire tous les calculs intermédiaires en conservant le signe « ,» et n’utiliser qu’à la fin , si cela est demandé, une valeur approchée.

Toutes les techniques de calculs ( à consulter ) dans un chapitre précédent sont utiles , mais la formule fondamentale est : a ² - b ² = ( a + b ) ( a - b)
En effet , si « a » ou « b » , ou les deux, sont des radicaux ( sous entendu : portant sur des radicandes entiers ou décimaux ) , « a² - b² » est entier ou décimal. Des expressions telles que :

et	et	et
Sont dites « conjuguées » …

Suite ….. » voir cours et exercices types @ ici….

2°) Travaux auto formatifs . ( ci-dessous)

TRAVAUX AUTO FORMATIFS.

CONTROLE

Que signifie: calculer le radical d’un nombre ?

La « racine » d’un nombre « X » est l’opération inverse de la puissance qui tend à trouver le nombre « x »de départ qui à permit de calculer X .

Donner l’écriture utilisée sur les calculatrices pour effectuer la recherche d’un radical d’un nombre.

= x = 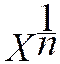;telle que et

Quelles sont les possibilités d’obtenir la valeur numérique de la racine n ^ième d’un nombre ?

Ecrire différemment les expressions suivantes : (forme d'écriture : puissance )


Rappel xⁿ
Ecriture avec le radical :
=
() ⁿ =
() ⁿ =
=
=
=
=
=
=
=
+ =
=
-=

Rappel xⁿ	Peut s'écrire =
Ecriture avec le radical :	Ecriture équivalente Sans radical	Développement ou simplification :	résultat
=	x
() ⁿ =	(x )ⁿ	x = x = x	x¹ = x
() ⁿ =	((x ⁿ ))ⁿ	((x )) = x	= x ⁿ
=	(x y )	x y
=	x y
=	()
=	()
=	= = x
=
=	Aucune transformation possible	(x + y)
+ =	Aucune transformation possible	x + y =
=	Aucune transformation possible	(x - y)
-=	Aucune transformation possible	x - y

EVALUATION:

Trouver les racines carrées parfaits des multiples de dix:

de 10⁰ à 10 ⁸

si elles existent ! pour 10⁰ ;10¹; 10²; 10³ ; 10⁴ ; 10⁵ ; 10⁶ ;10 ⁷ ; 10^8;

Première série d ’exercices :

soit un nombre « x » ; trouver la racine carrée du nombre :

x =0.25 ; =

x = 7,29 ; =

x = 33,64 ; =

x = 81 ; =

x = 291 600 ; =

x = 2 744 000 ; =

x = 1,574610⁸ ; =

II )Deuxième série d’exercices en relation avec la racine carrée d’un produit:

donc : ==

III ) Troisième série d’exercices en relation avec la racine d’un quotient:

Ces exercices utilisent des carrés parfaits

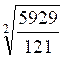Se ramener aux carrés parfaits; en se souvenant que tout nombre « à virgule » peut se mettre sous forme de fraction de dénominateur égal a ...........

IV ) Quatrième série d’exercices en relation avec la racine carrée d’une addition ou d’une soustraction , et les transformations

a) =

b ) =

c ) =

d ) =

e ) =

f ) =

g ) =

h ) =

k ) =

V ) Cinquième série d’exercices: Donner une valeur approchée d’une racine d’un nombre

1 ° ) Calculer les expressions suivantes avec la précision du dixième

2 ° ) Calculer les expressions suivantes avec la précision du centième

3 °) Calculer les expressions suivantes avec la précision du millième

= =

I ) remplacer dans les lettres par les nombres suivants et faire le calcul :

avec x= 16 et y = 9 (remarque : 16 et 9 sont des carrés parfaits; nous connaissons la racine carrée de 16 (4) et de 9 (3) , ces valeurs sont choisies pour faciliter la compréhension)


() ² =	() ² = 16
() ² =	() ² =16²= 256
=	==12
=	= = 4 3 = 12
=	»1,33333333
=	=»1,33333333
=	= = 0,25
=	= =0,25
=	= = 5
+ =	+ = 4+3 = 7
=	= = 2,6457513
=	== "Erreur"	Le calcul est impossible	On ne peut faire la racine carré d'un nombre négatif !
-=	-= 4 -3 = 1
-=	- = 3 - 4 = -1

II ) Transformer en vue de simplifier les calculs :


=	= =5 =	5
:	= = 2	2
=	= =	2x
=	=
=		= 5
=	=
+=	3 + 4 = 7

-	= 3-4
() ²	= 81

III) Résoudre :

: 7 =

7² = ()²

: 7² = 30+x

49 = 30+x

49 - 30 = x ; 19 = x ; conclusion « x » vaut 19

50 =

50² = ()²

50² =1600+x²

2500 - 1600 = x²

= 30

30 = x

CALCULS:

A ) Trouver les racines carrées parfaits des multiples de dixLmettre une croix dans la case correspondante


10⁰
10¹
10²	x
10³
10⁴	x
10⁵
10⁶
10 ⁷
10⁸	x

B ) soit un nombre « x » ; trouver la racine carrée du nombre :

	=
x =0,25		0,5
x = 7,29		2,7
x = 33,64		5,8
x = 81		9
x = 291 600		540
x = 2 744 000		1656,502339
x = 1,574610⁸		39681,22982

C )Deuxième série d’exercices en relation avec la racine carrée d’un produit:


=		4 fois 5 =20
=		=20
=		=56
=		=630
=		=1600
=		=600

D ) Troisième série d’exercices en relation avec avec la racine d’un quotient:

Ces exercices utilisent des carrés parfaits


=		1,6
=		1,5
=		7

E ) Se ramener aux carrés parfaits; en se souvenant que tout nombre « à virgule » peut se mettre sous forme de fraction de dénominateur égal a ...........

=		9,3
=		0,86

F ) Quatrième série d’exercices en relation avec la racine carrée d’une addition ou d’une soustraction , et les transformations


=		6,32455532
=		37,74917218
=		5,385164807
=		9,219544457
=		44,82186966
=		8,136952747
=		65
=		57
=		55

G ) Cinquième série d’exercices: Donner une valeur approchée d’une racine d’un nombre

1 ° ) Calculer les expressions suivantes avec la précision du dixième


=		2,2
=		4,1
=		69,0

2 ° ) Calculer les expressions suivantes avec la précision du centième


=		4,80
=		94,00
=		9,15

3 °) Calculer les expressions suivantes avec la précision du millième


=		9,434
=		9,7417
=		9,149
=		10,247
=		4,376
=		impossible =

H ) ENCADREMENT D’UN RESULTAT :

On donne le résultat des exercices suivants :

=4,4647451

=21,111276

=4,3742992

=4,717694

=2,6754054

= -3

Donner le résultat sous la forme: n < < n +1

ou n est un entier naturel et X un nombre (entier ou décimal )

: n	<	<	n +1
4			5
21			22
4			5
4			5
2			3
-4			-3

La racine de certain nombre est dit : nombre « incommensurable »

Exemple :

TRAVAUX AUTO FORMATIFS.

CONTROLE