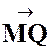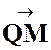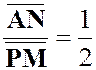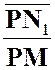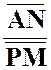La translation et "vecteurs"


COURS :

La translation est la transformation dans laquelle à tout point « M » d’une figure (F) on fait correspondre le point ( M’ ) , qui engendrera la figure ( F ‘ ) tel que : = « » est le vecteur donné. Voici les propriétés essentielles : a ) Les vecteurs définis par deux couples de points homologues dans ( F ) et ( F ‘ ) sont équipollents : = b) Deux courbes déduites l’une de l’autre par translation sont égales. c) Les tangentes à ces courbes en deux points homologues sont parallèles. d) La translation permet dans certains cas l’obtention de lieux géométriques. Il suffira, connaissant la courbe décrite par un point « M » , qu’un point « M’ » du lieu soit tel que : = ; étant un vecteur fixe.

Problème 1 :
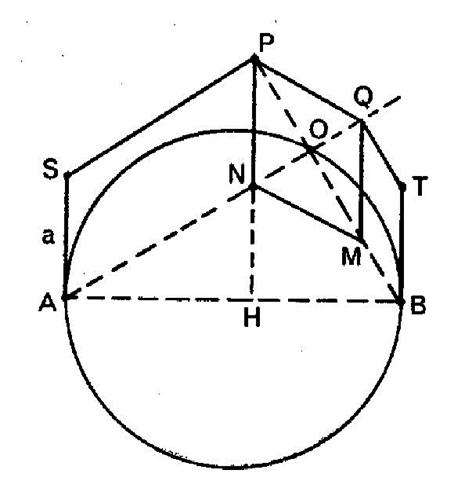
Un losange articulé « M N P Q » formé de quatre tiges rigides , se déforme dans son plan de manière que les diagonales « MP » et « NQ » passent constamment par deux points fixes « A » et « B » et que la direction des côtés « NP » et « MQ » soit constamment perpendiculaire à « AB » . 1°) Lieux des sommets de ce losange. 2°)Lieux des milieux des côtés. NB : La distribution des lettres « M N P Q » est celle de la figure.

Solution : Il convient d’abord de faire une figure soignée en prenant pour centre « O » du losange un point de la circonférence de diamètre « AB ». Soit « a » la longueur du côté du losange.
1°) Faisons subir au point « A » la translation de vecteur . Nous obtenons un point fixe « S » sur la tangente en « A » au cercle de diamètre « AB ». La figure « A S P N » est un parallélogramme . Donc . = = 1 droit. Le lieu du point « P » est sur le cercle de diamètre « SB ». Ce cercle passe par « A ».Il est décrit en entier par « P » parce que le point « O » décrit en entier le cercle de diamètre « AB ». Mais : = Le lieu de « N » se déduit du lieu de « P » par la translation de (orthogonale à « AB », dans le sens « SA », de grandeur « a ». Le lieu de « N » est un cercle égal au lieu de « P » passant par « A » et « B ». En faisant subir de même à « B » la translation = = , on voit que le lieu de « Q » est le cercle de diamètre « AT » , confondu avec le lieu de « P » parce que la figure « ASTB » est un rectangle.
Le lieu de « M » se déduit de celui de « Q » par la translation : = = C’est le même que le lieu de « N ». En résumé , les lieux cherchés , pour les sommets, sont les cercles circonscrits aux rectangles « ABST » et « ABS ’T ’ ». « S » , « T » sont obtenus en faisant subir « AB » la translation orthogonale à « AB » , et d’ intensité « a ». « S ’ » , « T ’ » sont obtenus en faisant subir « AB » la translation orthogonale à « AB » , et d’ intensité « - a »., le sens positif sur la perpendiculaire à « AB » étant « N P » .
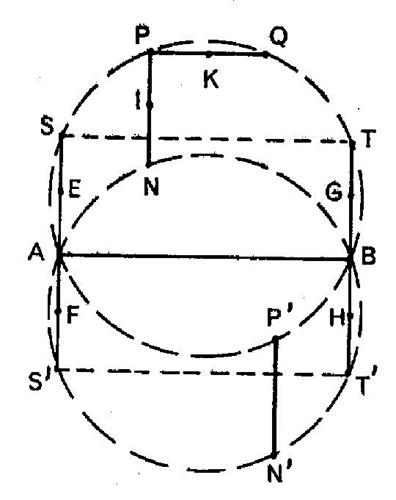
2°) Le lieu des milieux « I » et « J » de « PN » et « QM » sont déduits du lieu de « P » et « Q » par la translation . Il s’agit du cercle circonscrit au rectangle « E F H G » défini par les milieux de « SA » , « SA’ » , « B T’ » et « BT ». Le lieu des milieux « K » et « L » des côtés « PQ » et « NM » est celui des milieux des cordes de longueur constante « a » dans un cercle fixe. C’est un ensemble , de deux nouveaux cercles ayant pour centres les points de concours des diagonales des rectangles « A B S T » et « A B S ’ T ’ »
Problème 2 :
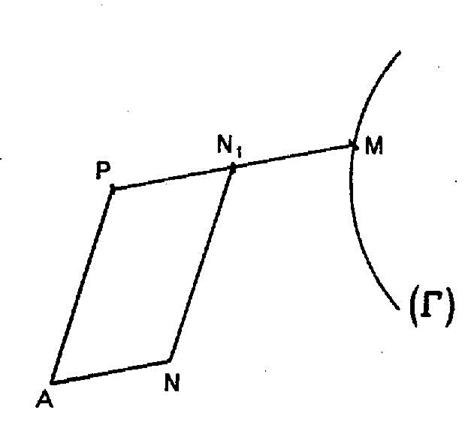
On joint un point fixe « P » au point « M » d’une courbe donnée ( ) . Par un autre point fixe « A », on mène la parallèle à « PM » sur laquelle on marque « N » tel que : lieu du point « N ». Indications : Faire subir à « N » la translation du vecteur . Il vient en « N₁ » tel que : = Le lieu de « N₁ » est une homothétique de ( ) « N » se déduit de « N ₁ » par la translation

Problème 3 :
Reprendre le problème précédent ; en précisant que ( ) est soit une droite, soit un cercle, et en variant la valeur numérique du rapport :
Problème 4
On donne deux parallèles ( D ) et ( ) et deux points « A » et »B » de part et d’autre de la bande de plan définie par ( D ) et ( ). Trouver ( D ) un point « N »tels que « M N » ait une direction donnée « » et que le chemin « A M + M N + N B » soit minimum.
Parfois la symétrie vient s’adjoindre à la translation.

Problème 5
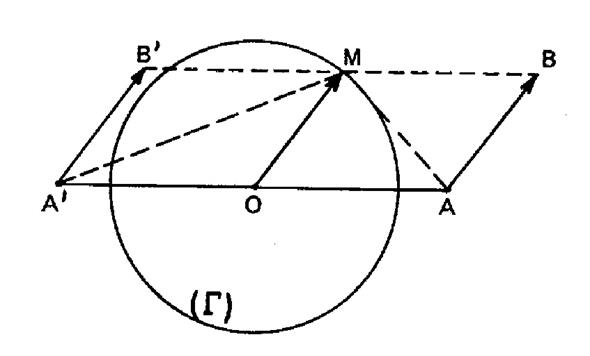
On considère un cercle fixe de centre « O » et deux points « A » et « A‘ »symétriques par rapports à « O »et extérieurs au cercle. Par un point « M » du cercle on mène les vecteurs équipollent à et équipollent à . 1°) lieux des points « B » et « B’ ». 2°) Lieux du symétriques « C » et « B » par rapport à « AM » et du symétriques « C’ » de « B’ » par rapport à « AM ’ » . 3°) « D » étant le point commun à « OM » et « AC » , montrer qu’il existe une relation simple entre « OD » et « AD ». ( travail niveau 4 : bac )

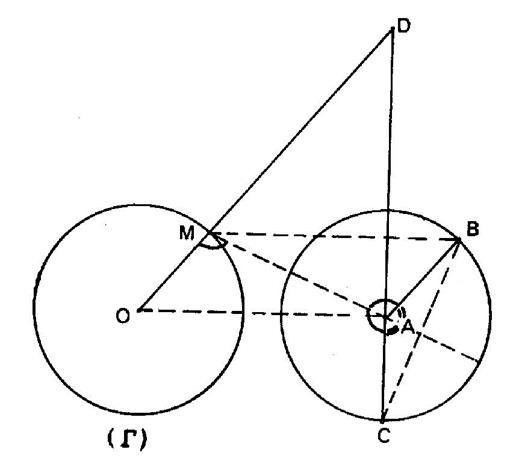
Solution : 1°) Soit « R » le rayon du cercle. Les équipollences = ; = . Entraînent les équipollences : = = et ceci montre que les lieux de « B » et « B’ » sont des cercles déduits du cercle ( ) donné par les translations ou 2°) « AM » étant le support d’un diamètre du lieu de « B » , le point « C » décrit le même cercle que « B ». De même « C ’ » décrit le même cercle par « B ’ ».
A cause de la symétrie : = ( relation 1 ) Mais le parallélogramme « M B A O »
	= =	( relation 2 ) ( relation 3 )
D’où par soustraction « membre à membre » : = ( relation 4 ) Ces angles sont d’ailleurs « alternes internes » : En comparant la relation 1 avec la relation 4
=
Le triangle AMD est isocèle : MD = AD Ou OD – R = AD OD – AD = R Comme il peut y avoir des cases de figure où OD est plus court que « A D » , nous adoptons pour relation :

Problème 6
Reprendre les mêmes données et résoudre les mêmes questions en supposant que les points « A » et « A ‘ » sont symétriques par rapport au point « O », mais intérieurs au cercle donné.

COURS (suite 1)
La translation est un moyen puissant pour réaliser des constructions .
Elle permet la résolution du problème suivant :
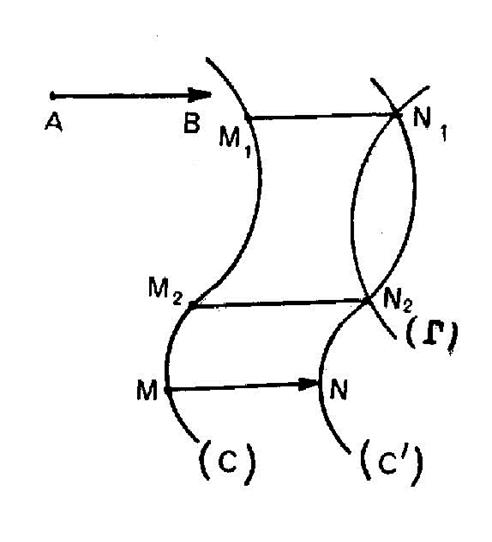
Entre deux courbes données : ( C ) et ( ) placée un segment « MN » parallèle à un segment donné « AB » et de même grandeur que « AB » . Solution : Nous faisons abstraction de la courbe ( ). Nous assujettissons le segment « MN » (voir vecteur MN) à être parallèle à un segment donné « AB » (voir vecteur témoin AB) de même grandeur et par exemple de même sens. C'est-à-dire opérons sur ( C ) la translation du vecteur . La courbe ( C ’ ) lieu de « N » devant être sur ( ) sera aux points communs à ( ) et à ( C ’ ) ; donc , sur la figure , en N ₁ ou N ₂ . Nota : Lorsque le sens « MN » n’est pas précisé, il y a lieu de faire subir à ( C ) les translations du vecteur AB et le vecteur BA , ce qui donne pour lieu de « N » deux courbes ( C ’ ) et ( C ’ ‘ ) . Dans de la figure ci contre ( C ’’ )ne couperait pas ( )
Problème 7
Reprendre le problème ci-dessus en spécialisant les courbes ( C ) et ( ) ; droite ou cercle ; et en supposant que « MN = 2 AB » ; « 3AB » , et en général « MN = AB » Indications : Faire subir à la courbe ( C ) la translation « » ou « » suivant le sens désiré…

Problème 8
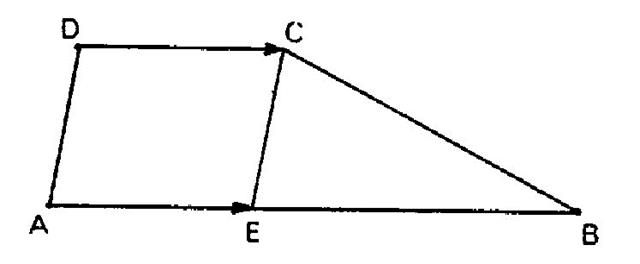
Construire un trapèze connaissant les longueurs des quatre côtés. Solution : Sur la figure d’étude « ABCD » ci contre faisons subir au point « A » la translation : qui l’amène en « E ». Désormais le triangle « ECB » peut être construit car on connaît les longueurs « CB » ; « CE = DA » et « BE = AB – AE » et « « AB –C D » , de ses trois côtés. Ce triangle construit , le trapèze s’achève en marquant « A » sur le prolongement de « BE » et en faisant subir la translation .

Problème 9
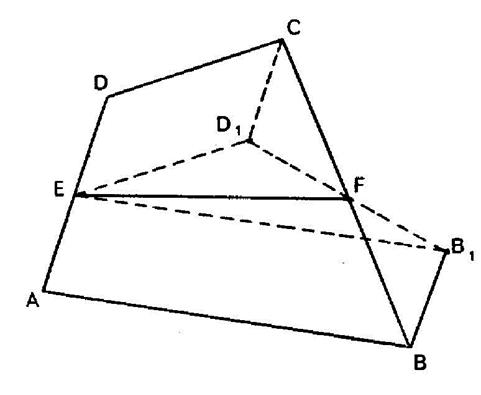
Construire un quadrilatère « ABCD » connaissant les longueurs des quatre côtés et le segment « EF » joignant les milieux de deux côtés opposés. Indications : Faire subir à « ED » la translation « » et à « EA » la translation « » ; « E » milieu de « AD » ; « F » milieu de « BC » Voir que les points D₁ F B₁ sont alignés. Construire le triangle E D₁ B₁ connaissant les longueurs de deux côtés et celle de la médiane comprise. Construire « C » et « B » . En déduire « A » et « D ».








TRAVAUX AUTO FORMATIFS.

CONTROLE


EVALUATION.
Refaire les problèmes…du cours …… ;;;;