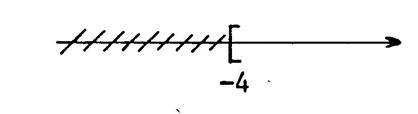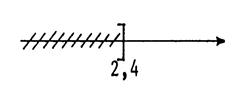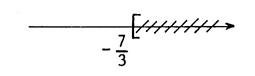Fiches sur les inéquations au collège classe de 4ème

Fiche 1 : Problème.
Un club d'achat de livres propose les deux options suivantes : Option A : abonnement 180 € par an et 55 € par livre acheté. Option B : abonnement 300 € par an et 40 € par livre acheté. 1°) Complète le tableau correspondant à un abonnement d'un an.
	Nombres de livres achetés	3	5	10	15
	Dépense avec l’option « A »
	Dépense avec l’option « B »
2°) En appelant « » le nombre de livres achetés en un an, Exprimez en fonction de « » la dépense (en €) avec l'option A : ………………………………………………. Exprimez en fonction de « » la dépense (en € ) avec l'option B. …………………………………………………..
3°) Pour quel nombre de livres la dépense est-elle la même pour les deux options ? Dans ces conditions on doit avoir Vous êtes en présence d'une équation. A toi de la résoudre. Réponse : la dépense est la même pour les deux options pour l'achat de ……….livres.
4°) Pour quels nombres de livres l'option A est-elle plus avantageuse que l'option B ? (La dépense avec l'option A doit être inférieure à la dépense avec l'option B.) On doit donc avoir . Vous êtes en présence d'une inéquation. Tout nombre mis à la place de pour lequel l'inégalité correspondante est vraie est appelé solution de l'inéquation. En utilisant le tableau de la première question, donne des solutions.
Résoudre une inéquation c'est trouver toutes les solutions de cette inéquation.

· Nous allons résoudre cette inéquation. En imaginant que représente une solution de l'inéquation, on est donc en présence d'une inégalité. On peut donc lui appliquer les règles de la leçon : … »ordre dans les nombres relatifs : fiche 5 et fiche 6 .
Retranchons « 180 » aux deux membres. On obtient : et après simplification il reste : Retranchons « » aux deux membres. On obtient : et après simplification il reste :

	Remarque Vous constatez que tout revient à transposer et , en changeant leur signe. On a donc .la même règle de transposition que pour les équations.
	Grâce à la règle du … »ordre dans les nombres relatifs : fiche 6 ., vous pouvez diviser par « 15 » les deux membres de l’inéquation : On obtient 15 ; c'est-à-dire Les solutions de l'inéquation sont donc les entiers strictement inférieurs à « 8 »
	Réponse à la question du problème : L'option A est plus avantageuse que l'option B pour l'achat de ……..livres.

	Fiche 2 : Exemples de résolution d’inéquations.	( voir : @ neutralisation d’un terme et d’un facteur)
	Exemple 1 Résolvons l'inéquation d'inconnue . Ajoutons « » aux deux membres (ce qui revient à transposer ). On obtient c'est-à-dire Les solutions sont tous les nombres supérieurs ou égaux à « »
	L'inéquation possède donc une infinité de solutions. Il n'est pas possible de nommer toutes ces solutions (comme dans la fiche 1), mais on peut en faire une représentation graphique à l'aide d'une droite graduée. (On barre ce qui ne convient pas) .
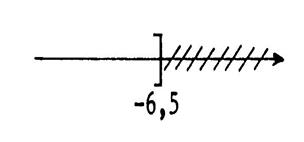
	Exemple 2 Résolvons l'inéquation 5y >12 d'inconnue y. Divisons les deux membres par 5, on obtient : 5y : >\2 : c'est-à-dire y> Représentation graphique : (Remarque la position du crochet).
	Représentation graphique :



	Exemple 4 : Résolvons l'inéquation d'inconnue « » . En divisant les deux membres d'une inégalité par un même nombre, on obtient une inégalité de même sens à condition que le nombre soit strictement positif . Or, ici, il faudrait diviser par -3 qui est « négatif ». On contourne cette difficulté en prenant les opposés. c'est-à-dire ; En divisant les deux membres par 3, on obtient		Représentation graphique.

	DIFFERENTES POSSIBILITES POUR LA REPRESENTATION GRAPHIQUE		( info : @ segment et bornes)



	Exercice 1 : Résolvez les inéquations suivantes. Faites la représentation graphique.
	A.
	B.
	C.
	D.

	Exercice 2 On donne un segment [AB] tel que en cm, AB = 7. On veut construire un triangle ABC tel que en cm, AC = 3. 1°) En appelant x la mesure (en cm) de la longueur de [BC], Déterminez les conditions que doit remplir pour que le triangle ABC existe (reportez-vous à la leçon …. ). Faites une représentation graphique (droite graduée ) 2°) Le triangle ABC peut-il être isocèle ? (précisez alors la base).

TRAVAUX AUTO _ FORMATIFS

CONTROLE :

Dans une inégalité si l’on multiplie ou divise par un nombre négatif que faut – il faire impérativement ?

EVALUATION :

EVALUATION

Devoir : (corrigé dans le cours)

	Exercices	solution
1-	2x < 23,4
2-	-1,5 "e 69
3-	3 ( x + 1 ) "e x - 2
4-	> 4

Série 2 :

Résoudre les inégalités suivantes :	Rendre compte de trois façons différentes.
4 x < 10
- 2 x £ 5
3x – 3 > 5x -5
3x – 5 > x + 4
2x -< x +
4x + > x + 4

Série 3.

	Résoudre :	Résolution
1-a	5x – 7 < 1
1-b	-2x + 2 < 5,7
1-c	8 ( 6x + 3) > 2x
1-d

Réponses : x "d ; x "e 1,5 ; x > ; x >

Résoudre le système suivant :

INTERDISCIPLINARITE

1°) Démontrer que la moyenne géométrique de deux nombres est toujours inférieure à la moyenne arithmétique de ces deux nombres.

2° ) Démontrer que la moyenne arithmétique de deux nombres est comprise entre ces nombres.

ACTIVITE Niveau 3^e :

(Pré requis : @ les équations du premier degré et @ les inégalités triangulaires ,et accès au corrigé)

Données :

ABC est un triangle dont les côtés ont pour mesure ( en cm).*

AB = 3x ; BC = 6 ; CA = 2x+1

Dans lequel « x » représente un nombre strictement positif.

1°) faire la figure dans le cas où « x » = 1,5

Placer [ BC ] ; puis AB = « ……… » ; CA = « …….. ».

2°) Pouvez- vous dessiner le triangle quand «x = 8 » ?

Commencer par calculer les côtés : AB = …….. ; CA = ……..

2°) Déterminer les valeurs de « x » pour lesquelles le triangle existe ( sans être aplati). Le triangle existe à condition que la longueur de chaque côté soit strictement inférieure à la somme des longueurs des deux autres côtés.

- AB < BC + CA se traduit par 3x < 6 + 2x +1 ; en transposant on obtient

3 x - 2x < 6 + 1 ; c’est à dire « x < …….»

- BC < CA + AB se traduit par 6 < …………….. ; en transposant on obtient

6 - 1< 2x + 3x ; c’est à dire « 5 < ………. »

et en divisant les deux membres par « 5 » on obtient : ……… < x

- AC < AB + BC se traduit par 2x +1 < ……………. ; en transposant on obtient

1 - 6 < ……….. ; c’est à dire « - 5 < x »

Ce qui est toujours vérifié puisque « x » est positif par hypothèse.

- En définitive le triangle existe quand 1 < x et x > 7 c’est à dire …..….. < x < ……

4°) Pour quelle valeur de « x »le périmètre du triangle est-il égal à 32 cm ?

5°) Pour quelle valeur de « x », le triangle est -il isocèle ?

- de base [ BC] ; AB = CA

- de base [ BC]

6°)

- Pour quelle valeur de « x » ; CA = 2 AB ?

- Pour quelle valeur de « x », CA = 2 BC ?

- Pour quelle valeur de « x » ; CA = AB ?

7°) Se peut -il que le double de AB soit égal au triple de AC diminué de la moitié de BC ?

Résoudre les inéquations suivantes :

1°) Résoudre l’inéquation 3x – 5 2 x + 8

2°) Résoudre l’inéquation 7x + 4 4 x + 19

3°) Résoudre l’inéquation 2x – 8 < x – 7