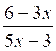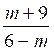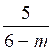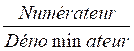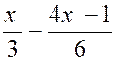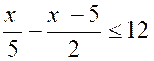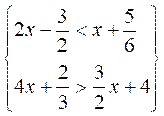|
Inéquation ou
inégalités (définitions) |
|
|
Les Segments et
droites graduées |
|
|
Les intervalles |
|
|
Les demi droites |
ENVIRONNEMENT du dossier:
|
Index warmaths |
Objectif
précédent : |
Objectif
suivant : 1°) inéquation et régionnement
(généralités) en x et y (suite+++) |
|
|
|
|
|
|
DOSSIER : LES
« INEQUATIONS » du premier degré à une inconnue : ( niveau 4 )
B)
Inéquation du premier degré
C) Inéquation a une inconnue dont la résolution se ramène à celle d’inéquation du premier degré.
D ) SIGNE
DU BINOME DU PREMIER DEGRE.
E)
Inéquations qui renferment des dénominateurs contenant l’inconnue.
F)
Système d’inéquations ou Inéquations simultanées.
|
TEST |
COURS
|
Interdisciplinarité |
|
En faisant
passer tous les termes dans un même , toute inéquation peut se mettre sous
l’une des deux formes :
P > 0 ou P
< 0
Si
« P » est un polynôme, on dit
que l’inéquation est entière et le degré
de « P » est le degré de l’inéquation.
b) Inéquation du premier degré :
D’après
ce qui précède, une inéquation du premier degré est de la forme P > 0 ou P< 0 ,P étant le polynôme du
premier degré.
Si l’on
fait passer tous les termes contenant l’inconnue « x » dans le
premier membre et tous les autres dans le second, on obtient une inéquation de
la forme :
a
x > b ou a x < b
« a »
et « b » étant des données.
Leur
résolution est immédiate.
Soit par exemple la première inéquation : a x
> b
1°) si a > 0 ;
x > ![]()
2°) si
a < 0 ; x < ![]()
3°) si
a = 0 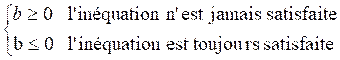
Remarque : Si une inéquation du premier degré
renferme des paramètres, on sera en général amené à distinguer plusieurs cas ,
car , suivant les valeurs des paramètres , le coefficient « a » de
l’inconnue sera positif , négatif ou nul et , dans chacun de ces ca, on a un
résultat différent .
Exemple I : Résoudre l’inéquation :
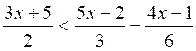
Chassons
les dénominateurs. On obtient :
3 ( 3x +5)
< 2 ( 5x - 2 ) - ( 4x -1)
9 x + 15 <
6x - 3
3x
< - 18
x <
- 6
Exemple II Résoudre
l’inéquation : m ( x + 2) + 2 x
> 3 ( 3x - 5 )
« m » étant un paramètre et « x »
l’inconnue..
Cette
inéquation est équivalente à :
m x + 2m + 2x > 9x - 15
1°) Si
m > 7 , on peut diviser les deux
membres par m - 7 qui est positif et on
obtient :
x >
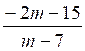
ce qui
peut s’écrire : x > 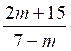
2°) Si
m < 7 , on peut encore diviser les
deux membres par « m-7 » qui
est négatif, mais il faut changer le sens de l’inéquation, ce qui donne :
x < 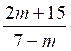
3°) Si m = 7, l’inéquation s’écrit 0 × x > 14 - 15
Elle
est donc toujours satisfaite.
c)
Inéquation a une inconnue dont la résolution se ramène à celle
d’inéquation du premier degré.
I)
Inéquations entières : nous avons
vu dans le « chapitre « C » @ des
équations » que pour résoudre
une équation entière on fait passer les termes dans un même membre.
L’équation
étant ainsi mise sous la forme « P = 0 » on essaie de mettre
« P » sous la forme d’un produit de facteurs.
Pour
résoudre une inéquation entière on procède de façon analogue. On fait
passer tous les termes dans un même
membre. L’inéquation étant ainsi mise sous la forme P > 0 ou P< 0 , on essaie de mettre
« P » sous la forme d’un produit de facteurs du premier degré.
Par
exemple, s’il est possible de mettre « P » sous la forme d’un produit
de trois facteurs du premier degré A ; B ; C l’inéquation
s’écrit :
A × B ×
C > 0
ou A × B × C < 0
Pour
résoudre cette inéquation, on étudiera les signes des différents facteurs
A ; B ; C on en déduira le signe de leur produit suivant les valeurs
de l’inconnue , donc les solutions de l’inéquation.
Afin de
présenter les calculs plus commodément, on dispose les résultas dans un tableau.
Dans
une première ligne on met les valeurs de l’inconnue « x » pour
lesquelles A ; B ; C change de
signe, ces valeurs étant rangées par ordre de grandeur croissante. On obtient
ainsi des intervalles dans lesquels A ; B ; C ont le même signe.
Dans les lignes suivantes, on étudie les signes
de A ; B ; C dans chacun des intervalles. De ces signes on
déduit le signe du produit A × B × C , donc les valeurs de « x » pour lesquelles l’inéquation est satisfaite.
Exemple : Résoudre
l’inéquation : ( 2x - 3 ) ² >
( 5x - 6 ) ²
Cette
équation s’écrit :
( 2 x - 3 ) ² - ( 5x - 6 )
² > 0
( 2x - 3 + 5 x - 6 ) ( 2x - 3 -5x +6 ) > 0
( 7x - 9 ) ( -3 x + 3 ) > 0
( 7 x - 9 ) ( x -
1) <
0
7x - 9
> 0 donne : 7
x > 9 c’est à dire x > ![]()
x -1 >
0 donne : x
> 1
Nous
mettrons donc dans le tableau les valeurs
![]() et 1 ; ce qui
nous donne les résultas suivants :
et 1 ; ce qui
nous donne les résultas suivants :
|
x |
-x |
1 |
|
|
x |
||
|
7x - 9 |
- |
|
|
- |
0 |
+ |
|
|
x -
1 |
- |
0 |
+ |
|
|
+ |
|
|
(7x-9) (x-1) |
+ |
|
|
- |
|
|
+ |
D’où
les solutions de l’inéquation : 1
< x < ![]()
D )
SIGNE DU BINOME du premier degré
Dans
l’exemple précédent nous avons eu à étudier le signe de différents facteurs du
premier degré.
On peut
se proposer d’étudier d’une façon
générale le signe d’un binôme du premier degré : y = a x
+ b
On peut
écrire : y = a ( x ![]() )
)
Si x > - ![]() on a x +
on a x +![]() > 0 ; donc « y »
a le signe de « a »
> 0 ; donc « y »
a le signe de « a »
Si x < - ![]() on a x +
on a x + ![]() < 0 ; donc « y » a le signe de
« -a »
< 0 ; donc « y » a le signe de
« -a »
x = - ![]() s’appelle la « racine du binôme « a x+b »
s’appelle la « racine du binôme « a x+b »
Nous
sommes ainsi conduits aux résultats suivants :
Définition : on
appelle « racine d’un binôme du premier degré » la racine de l’équation obtenue en égalant ce
binôme à zéro.
Théorème :
Le binôme du premier degré
« a x+b » a le signe de « a » pour les valeurs de
« x » supérieures à sa racine et le signe de « -a » pour
les valeurs inférieures.
Ce théorème
permettra de déterminer immédiatement le signe des différents binômes du
premier degré sans avoir à résoudre des inéquations, comme on l’a fait dans
l’exemple précédent (Résoudre l’inéquation : ( 2x - 3 ) ² > ( 5x - 6 ) ²)
E) INEQUATION QUI RENFERMENT DES DENOMINATEURS CONTENANT
L’INCONNUE.
Si une
équation renferme des dénominateurs contenant l’inconnue, on ne les chasses
pas. Aprés avoir fait passer tous les termes dans un même membre et réduit au même dénominateur on obtient une inéquation de la forme :
![]() > 0 ou
> 0 ou ![]() < 0
< 0
Le signe du quotient ![]() étant le même que
celui du produit A . B ;
pour résoudre ces inéquations il suffit de résoudre les inéquations :
étant le même que
celui du produit A . B ;
pour résoudre ces inéquations il suffit de résoudre les inéquations :
A . B > 0 et
A . B >0
On est
ainsi ramené à la résolution d’une inéquation entière.
EXEMPLE 1 : Résoudre l’inéquation : 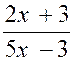 < 1
< 1
Cette
inéquation est équivalente à :
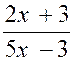 - 1 < 0
- 1 < 0
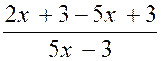 < 0
< 0
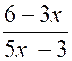 < 0
< 0
|
x |
-x |
|
|
2 |
x |
||
|
6 - 3x |
+ |
|
|
+ |
0 |
- |
|
|
5x - 3 |
- |
0 |
+ |
|
|
+ |
|
|
|
- |
|
|
+ |
|
|
- |
D’où les solutions de l’inéquation : x < ![]() et x > 2
et x > 2
EXEMPLE
II : Résoudre l’inéquation : 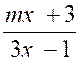 < 2
< 2
Cette inéquation est équivalente à :
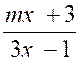 - 2 < 0
- 2 < 0
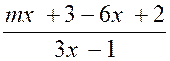 < 0
< 0
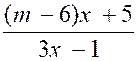 < 0
< 0
Pour étudier le
signe du dénominateur il nous faut distinguer plusieurs cas suivant que le
coefficient de « x »
est positif , négatif ou nul.
D’autre part, ce signe dépend de la position du nombre « x » par rapport à la
racine qui est égale à 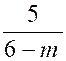 .
.
Quant au dénominateur, son signe dépend de la
position du nombre « x » par rapport à sa racine qui est ![]()
Il faut
donc savoir quelle est la plus petite de
ces deux racines ; pour cela étudions le signe de leur différence.
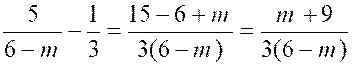
|
m |
-z |
-9 |
|
6 |
z |
|||
|
m + 9 |
- |
0 |
+ |
|
|
+ |
||
|
6 - m |
+ |
|
|
+ |
0 |
- |
||
|
|
- |
|
|
+ |
|
|
- |
|
|
|
|
|
|
. |
|
|
|
|
Finalement,
nous voyons qu’il faut distinguer plusieurs cas suivant la position de
« m » par rapport aux nombres
« -9 » et « 6 ».
1°) m < -9
|
m |
-z |
|
|
|
z |
|||
|
Numérateur |
+ |
0 |
- |
|
|
- |
||
|
Dénominateur |
+ |
|
|
+ |
0 |
- |
||
|
|
- |
|
|
+ |
|
|
- |
|
2°) -9 < m < 6
|
m |
-z |
|
|
|
z |
||
|
Numérateur |
+ |
|
|
+ |
0 |
- |
|
|
Dénominateur |
- |
0 |
+ |
|
|
+ |
|
|
|
- |
|
|
+ |
|
|
- |
3°) m > 6
|
m |
-z |
|
|
|
z |
||
|
Numérateur |
- |
0 |
+ |
|
|
+ |
|
|
Dénominateur |
- |
|
|
- |
0 |
+ |
|
|
|
+ |
|
|
- |
|
|
+ |
Cas limites :
1°) m =
- 9 . L’inéquation s’écrit : 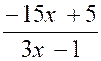 < 0
< 0
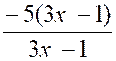 < 0
< 0
L’équation
est toujours satisfaite .
2°) m = 6 L’inéquation s’écrit : 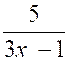 < 0
< 0
3x - 1 < 0
x < ![]()
En résumé :
m < -9 : x < 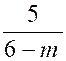 ou x >
ou x >
![]()
- 9
< m < 6 : x
< ![]() ou x <
ou x < 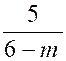
m > 6 : : 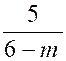 < x
<
< x
< ![]()
m = - 9 :
l’inéquation est toujours satisfaite.
m = 6 : x
< ![]()
|
|
Résoudre un système
d’inéquations simultanées à une inconnue, c’est trouver les valeurs de cette
inconnue qui satisfont à la fois à toutes ces inéquations.
Pour résoudre
un tel
système , il suffit de résoudre successivement toutes les inéquations données et de conserver
les solutions communes.
Pour cela, si le
résultat n’est pas immédiat, il peut être commode de ranger par ordre de grandeur croissante les valeurs limites
trouvées. On détermine ainsi un certain
nombre d’intervalles. On barre ceux dans
lesquels l’inconnue ne doit pas se trouver. Les
intervalles non barrés donnent les solutions du système.
Exemple I :
résoudre le système :
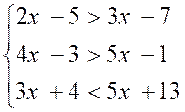
1ère
équation : -x > -2 c’est à dire « x < 2 »
2ème
équation - x > 2 c’est à dire x < -2
3ème
équation - 2x < 9 c’est
à dire x > 4,5
Le résultat est
immédiat : -4 , 5 < x
< -2
Exemple II . Résoudre le système :
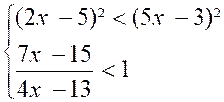
1ère
inéquation : (on ramène le premier membre sous forme d’un produit)
( 2x - 5)² - (5x-3)² <0
( 2x - 5 +5x -3) ( 2x -5 -5x +3) <0
(7x -8) (-3x -2) < 0
Tableau
|
x |
-x |
|
|
|
x |
||
|
7x -8 |
- |
|
|
- |
0 |
+ |
|
|
-3x -2 |
+ |
0 |
- |
|
|
- |
|
|
(7x-8)(-3x-2) |
- |
|
|
+ |
|
|
- |
Résulta : x < ![]() ou x >
ou x >
![]()
2ème
Inéquation : 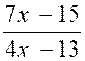 < 1
< 1
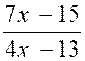 - 1 < 0
- 1 < 0
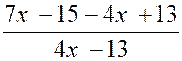 <0
<0
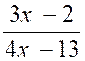 < 0
< 0
tableau :
|
|
-x |
|
|
|
x |
|||
|
3x-2 |
- |
0 |
+ |
|
|
+ |
||
|
4x-13 |
- |
|
|
- |
0 |
+ |
||
|
|
+ |
|
|
- |
|
|
+ |
|
Résultat : ![]() < x <
< x < ![]()
Rangeons les différentes valeurs trouvées par
ordre de grandeur croissante et barrons (grisons) les intervalles dans lesquels « x »
ne doit pas se trouver.
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
||||
D’où les solution du système : ![]() < x <
< x < ![]()
TRAVAUX AUTO
FORMATIFS.
CONTROLE :
Dans
une inégalité si l’on multiplie ou divise par un nombre négatif que faut – il
faire impérativement ?
EVALUATION
Devoir : (corrigé dans le cours n°1 )
|
|
Exercices |
Solution : |
|
1- |
2x < 23,4 |
|
|
2- |
-1,5 >
69 |
|
|
3- |
3 ( x + 1 ) >
- 2 |
|
|
4- |
|
|
Série
2 :
|
Résoudre
les inégalités suivantes : |
Rendre compte de
trois façons différentes. |
|
a) 4 x < 10 |
|
|
b) - 2 x £ 5 |
|
|
c)
3x – 3 > 5x -5 |
|
|
d)
3x – 5 > x + 4 |
|
|
e)
2x - |
|
|
f)
4x + |
|
Série
3.
|
|
Résoudre : |
Résolution
|
|
1-a |
5x - 7 "e 1 |
|
|
1-b |
-2x + 2 < 5,7 |
|
|
1-c |
8 ( 6x + 3) >
2x |
|
|
1-d |
|
|
Réponses :
x "d ; x "e
1,5 ; x > ![]() ; x >
; x > ![]()
Série 3 :
a)
Résoudre l’inéquation : ( 2x -
5)²< ( 5x - 3)²
b)
Résoudre l’inéquation : 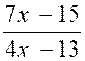 < 1
< 1
Série 4
Résoudre
les systèmes suivant :
1°) Résoudre le système :
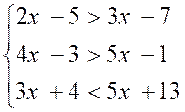
2°) Résoudre
le système
|
|
|
3°)
Résoudre le système :
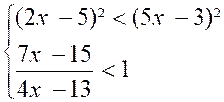
1°) Démontrer que la moyenne géométrique de deux
nombres est toujours inférieure à la moyenne arithmétique de ces deux nombres.
2°
) Démontrer que la moyenne arithmétique de deux nombres est comprise entre ces
nombres.
ACTIVITE Niveau 3e :
(Pré requis : @
les équations du premier degré et @ les inégalités triangulaires ,et accès au corrigé)
Données :
ABC
est un triangle dont les côtés ont pour
mesure ( en cm).*
AB
= 3x ; BC = 6 ; CA = 2x+1
Dans
lequel « x » représente un nombre strictement positif.
1°) faire la figure dans le cas où
« x » = 1,5
Placer [ BC ] ; puis AB = « ……… » ;
CA = « …….. ».
2°)
Pouvez- vous dessiner le triangle quand «x = 8 » ?
Commencer
par calculer les côtés : AB = …….. ; CA
= ……..
2°)
Déterminer les valeurs de « x » pour lesquelles le triangle existe (
sans être aplati). Le triangle existe à condition que la longueur de chaque
côté soit strictement inférieure à la somme des longueurs des deux autres
côtés.
-
AB < BC + CA se traduit par 3x < 6 + 2x +1 ; en transposant on
obtient
3 x - 2x < 6 + 1 ; c’est
à dire « x <
…….»
-
BC <CA + AB se traduit par 6 <
……………..
; en transposant on obtient
6 - 1< 2x + 3x ; c’est
à dire « 5 <
………. »
et
en divisant les deux membres par « 5 » on obtient : ………
< x
-
AC < AB + BC se traduit par 2x +1 < …………….
; en transposant on obtient
1 - 6 < ……….. ;
c’est à dire « - 5 < x »
Ce
qui est toujours vérifié puisque « x » est positif par hypothèse.
-
En
définitive le triangle existe quand 1
< x et x > 7 c’est à dire …..….. < x < ……
4°)
Pour quelle valeur de « x »le périmètre du triangle est-il égal à 32
cm ?
5°)
Pour quelle valeur de « x », le triangle est -il isocèle ?
-
de base [ BC] ; AB = CA
-
de base [ BC]
6°)
-
Pour quelle valeur de « x » ; CA = 2 AB ?
-
Pour quelle valeur de « x », CA = 2 BC ?
-
Pour
quelle valeur de « x » ; CA = ![]() AB ?
AB ?
7°) Se peut -il que le double de AB soit égal au triple de AC diminué de la
moitié de BC ?