|
Les Segments et droites graduées |
|
|
Les intervalles |
|
|
Les demi droites |
|
ENVIRONNEMENT du dossier:
|
Objectif précédent : Les inégalités (info)
|
Objectif suivant : 1°) Suite sur les systèmes d’inégalités du premier
degré à une inconnue |
DOSSIER : SYSTEME d’ INEQUATIONS du premier degré à une inconnue
|
TEST |
COURS
|
Devoir Contrôle |
Devoir évaluation |
Interdisciplinarité Info
>>>> INTERDISCIPLINARITE
|
|
Corrigé Contrôle |
Corrigé évaluation
|
Systèmes d’inégalités :
On peut proposer un système de deux inégalités . Les solutions du système sont les valeurs de
« x » qui satisfont à la fois aux deux inégalités .
Exemple : Soit le système :
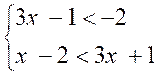
a) la première inégalité devient
successivement :
3x -1 <
-2
3x
< -2 + 1
3x
< - 1
x
< 
( - 0,33333)
b) la deuxième inégalité devient
successivement :
x-2 <
3x +1
x-2
- 1 <
3x
x-
3 <
3x
-3 <
3x –x
-3 <
3x –x
-3 <
2x
< x
-
1,5 <
x
discussion
« x » doit donc d’une part être inférieur à ;
d’autre part être supérieur à -
1,5 ; il n’y a pas contradiction
|
interprétation graphique : |
Soit un axe orienté , les points dont les abscisses
vérifient l’inéquation
|
|
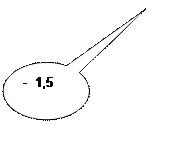
Les solutions du système sont les nombres compris
entre et - 1,5 ce que l’on peut écrire par la
double inégalité :
Conclusion : >
x >- 1,5 ou
-1,5 < x < -1/3
Question :
Quelle
valeur de « x » vérifie le système ?
3x
-1 < -2
x-2
< 3x +1
on
propose :
|
A |
B |
C |
D |
|
x = - 5/3 |
x = - 2 /3 |
x = - 8 / 5 |
x =- 1/5 |
|
On calcule la valeur décimale : sachant que -1,5 < x < -1/3 ; ou -1,5 < x
< - 0,3333 |
|||
|
- 1,6666 |
Valeur retenue : - 0,6666 |
- 1,6 |
- 0,2 |
Résoudre un système d’inéquations :
Résoudre un système d’inéquations ( dit aussi
inéquations simultanées) à une inconnue, c’est trouver les valeurs de cette
inconnue qui satisfont
à la fois à toutes ces
inéquations.
Pour résoudre un tel système , il suffit
de résoudre successivement toutes les inéquations données et de conserver les solutions communes.
Pour cela, si le résultat n’est pas immédiat, il peut être commode de
ranger par ordre de grandeur croissante
les valeurs limites trouvées. On détermine ainsi un certain nombre d’intervalles. On barre ceux dans lesquels
l’inconnue ne doit pas se trouver. Les intervalles non barrés donnent les solutions du système.
Exemple : résoudre le
système :
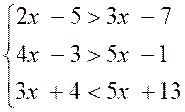
1ère équation : -x > -2 c’est à dire « x < 2 »
2ème équation - x
> 2 c’est à dire x < -2
3ème équation - 2x
< 9 c’est à dire
x > 4,5
Le résultat est immédiat : - 4 , 5 < x < -2
CONTROLE :
Donner la procédure qui permet de résoudre un
système d’inéquations du premier degré.
EVALUATION
Quelle valeur de
« x » vérifie le système suivant :
1°) Quelle valeur de « x » vérifie le système
suivant :
(on dit aussi )
Résoudre : 