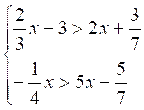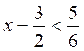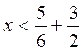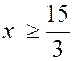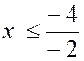|
Les Segments et
droites graduées |
|
|
Les intervalles |
|
|
Les demi droites |
|
|
|
ENVIRONNEMENT du
dossier:
|
|
|
|
|
|
Objectif précédent : |
DOSSIER : SYSTEME d’ INEQUATIONS du premier degré à une inconnue.
- par le calcul.
- Avec la solution
graphique
-
|
TEST |
COURS |
Interdisciplinarité |
|
COURS:
A) Solution par le calcul…..
Par définition : résoudre un système d’inéquations c’est trouver les valeurs de « x » qui
satisfont à la fois à toutes ces
inéquations
Ainsi , lorsque l’on doit résoudre un système de deux inégalités.
Les solutions du système sont les valeurs de « x » qui
satisfont à la fois aux deux inégalités.
Exemple 1 :
Soit le système : 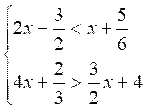
La première inégalité devient successivement :
|
|
|
|
|
|
|
|
|
|
x< |
|
La deuxième inégalité devient :
4x - 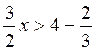
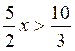
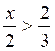
x >
![]()
« x »
doit donc d’une part être inférieur à ![]() , d’autre part
supérieur à
, d’autre part
supérieur à ![]() , il n’y a pas
contradiction.
, il n’y a pas
contradiction.
Les
solutions du système sont les nombres compris entre ![]() et
et ![]() ,
,
ce que l’on peut écrire par la double égalité : ![]() < x <
< x < ![]() ;
;
Ce qui
se lit : « x » compris entre ![]() et
et ![]() ;
;
Remarque. -
Il
peut se faire que les conditions auxquelles « x » doit satisfaire
soient contradictoires ; dans ce cas le système est « impossible ».
Exemple 2 :
Résoudre le système : 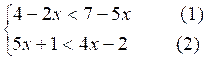
L’inéquation (1) a pour solution x <1
et l’ inéquation (2)
a x < -3
L’intervalle non barré donne pour
solution du système x < - 3
Exemple 3 :
Résoudre le système : 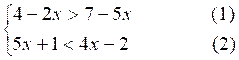
L’inéquation (1) a pour solution
x > 1 ; l’inéquation (2) a
pour solution x < -3 .
Conclusion :le système
proposé n’ a pas de solution.
Exemple 4 :
Résoudre :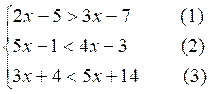
On résout séparément chacune de ces inéquations, nous
obtenons :
x < 2 (1)
; x < - 2 (2)
; x > - 5 (3)
solution graphique : Marquons sur
un axe xx’ les points correspondants à
ces nombres et barrons les valeurs de « x » qui ne conviennent pas à
chacune des inéquations . L’intervalle non barré [ -5 ; - 2 ]
sont les solutions du
système ; soit : -5 < x < - 2
B) Solution par le calcul et le graphique…..
La représentation graphique permet de
visualiser plus clairement l’expression de cette solution.
On reprend la
résolution des deux inéquations vu
précédemment !!!
|
Exemple 1 |
|
|
|
|
:
Résoudre le système suivant : |
|
|
|
Résoudre l’inéquation (1) 3x – 5 |
|
|
|
Résolution : 3x – 2 x x
|
Résolution pratique :: on ajoute « -2x » dans chaque membre. 3x – 5 – 2 x 3x – 5 – 2 x on ajoute « +5 » dans
chaque membre : 3x – 5 + 5 – 2 x on obtient : 3x + 0 – 2 x |
|
|
Représentation
graphique des solutions : |
|
|
|
Remarquez que le crochet indique que la
valeur « 13 » est incluse comme solution…. |
|
|
|
Résoudre l’inéquation (2) 7x + 4 |
|
|
|
Après une double
transformation : 7x – 4 x Ensuite après
« regroupement »
: 3x Soit : x |
Après réduction…. |
|
|
Remarquez que le crochet indique
que la valeur « 5 » est incluse comme solution…. |
|
|
|
En résumé : les deux solutions
sont : x 5 On représente sur le même axe les deux solutions : |
|
|
|
|
|
|
|
|
|
|
Exemple 2 : |
|||
|
|
Résoudre le système
suivant : |
||
|
|
Résoudre l’inéquation (1) : 3 x +
5 |
|
|
|
|
Après une
double transformation : 3 x + 5 x |
|
|
|
|
après
« regroupement , on obtient : 8 x
|
|
|
|
|
Soit la solution x |
||
|
|
|
||
|
|
Résoudre l’inéquation (2) : 2x –
8 < x – 7 |
|
|
|
|
Après une
double transformation : 2x – x < -7 + 8 Ensuite ;
après « regroupement » : x < 1 |
|
|
|
Soit la solution : x < 1 |
|||
|
|
Remarquez que le crochet indique
que la valeur « 1 » est exclue comme solution….
|
||
|
|
Solution
finale : x < 1 |
|
|
|
|
Soit la
représentation graphique :
L’ensemble des solutions est
représenté par la partie non hachurée de la droite. |
||
|
|
|
|
|
|
Exemple 3 |
|||
|
|
Résoudre le
système d’inéquation : |
||
|
|
Résoudre l’inéquation (1) - 4 x + 4 - 4 x + 6 x 2 x
x
|
|
|
|
|
|
|
|
|
|
Résoudre l’inéquation (2) x -
5 x - 3 x
- 2 x
x |
|
|
|
|
|
|
|
|
|
Regroupement des résultats : |
|
|
|
|
la droite ne présente pas de
partie non hachurée. Conclusion : le système
n’admet pas de solution. |
|
|
|
|
|
|
|
TRAVAUX AUTO FORMATIFS.
CONTROLE :
Que signifie « résoudre un système
d’inéquations» ?
R- résoudre un système
d’inéquations c’est trouver les valeurs
de « x » qui satisfont à la fois
à toutes ces inéquations.
Série 1 :
(systèmes traités dans le cours)
A ) Résoudre
le système : 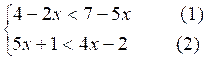
B ) Résoudre
le système : 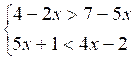
C)
Résoudre le système suivant : 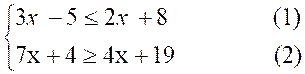
D) Résoudre le système suivant : 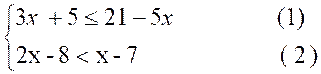
E)
Résoudre le système d’inéquations :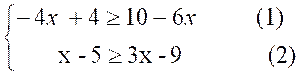
F)
) Résoudre :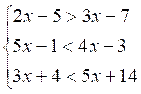
Série 2
A ) Résoudre :
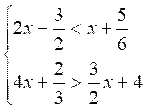
B) Résoudre : 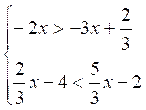
C) Résoudre :