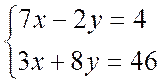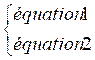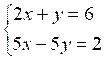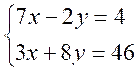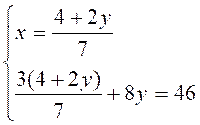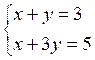|
|
|
|
Les
inégalités et inéquations (définitions) du premier degré |
ENVIRONNEMENT du dossier:
|
Objectif précédent
|
Objectif suivant : |
1°) Voir
le résumé « basique » |
DOSSIER (algèbre) : « LES SYSTEMES »
définitions
|
TEST |
COURS
|
Devoir Contrôle |
Interdisciplinarité |
|
Corrigé Contrôle |
Corrigé évaluation
|
|
Formulaire |
COURS
SYSTEME :
lorsque plusieurs inconnues doivent satisfaire à la fois plusieurs équations , l’ensemble de ces équations forme ce que l’on
appelle : un système d’équations
simultanées.
Remarque : On ne peut
parfois résoudre directement un système d’équations il faut donc transformer ce
système en un autre système . on obtient donc un
deuxième système .
On dit que deux systèmes
d’équations simultanées sont équivalents quand ils admettent les mêmes solutions.
Systèmes équivalents.
On dit que
deux systèmes sont équivalents
lorsqu’ils admettent les mêmes solutions , c’est à
dire lorsque toute solution du premier est solution du second et que toute
solution du second est solution du premier.
Remarque : la méthode suivi pour résoudre une
équation du premier degré à une inconnue
revient au fond à remplacer cette
équation par une équation équivalente plus simple ; de même pour résoudre
un système d’équations du premier degré à plusieurs inconnues
, on cherche à le remplacer par un système
équivalent plus simple.
Résoudre un système d’équations simultanées
Résoudre
un système d’équations simultanées , c’est trouver
toutes les valeurs qui , mises à la place des inconnues dans toutes les équations
du système , transformes ces équations en identités.
Remarque :
Eliminer une
lettre entre plusieurs équations , c’est former un
nouveau système d’équations équivalent au premier et dans lequel toutes les
équations , sauf une , ne contient plus cette lettre.
Les
deux principes démontés pour les
équations à une inconnue , s’appliquent aux équations
à plusieurs inconnues , de la même manière , il faut maintenant en établir un
autre .
|
Rappels : 1°) Si aux deux membres d’une équation on ajoute une même quantité , on forme une équation équivalente à la première. Dans le cas d’une résolution
toute solution de la nouvelle équation est solution de l’équation de départ. 2°)Si on multiplie les deux membres d’une
équation par une équation par une quantité
qui n’est pas nulle et qui ne contient pas l’inconnue , on forme une nouvelle
équation équivalente à la première. |
Représentation mathématique d’un système :
On
écrit les équations l’une en dessous de l’autre on les réunis
par une accolade à gauche des équations.
|
exemple |
Application : |
|
|
|
Principe
relatif à la transformation d’un système d’équations en un autre système
équivalent.
|
Etant donné un système
d’équation simultanées du premier degré , si on prend dans l’une des
équations la valeur de l’une des inconnues , de « x » , par exemple
, en faisant les calculs comme si les autres étaient connues , et si on
remplace « x » par cette expression
obtenue , dans toutes les autres équations , on forme un nouveau
système équivalent au système proposé. |
|
Exemple : Prenons , par exemple un système de deux équations simultanées du premier
degré. I ) de la première équation , on déduit, en considérant
« y » comme un nombre connu. 7x = 4 + 2y ou x = on remplace « x » par l’expression
ainsi obtenue dans la deuxième équation et on a : 3( Le système des deux équations ( II ): I I )
Est équivalent au système I |
1°)
Toute solution du système I est solution du système II
Supposons que
deux nombres mis à la place de « x » , et l’autre à la place de
« y » , dans l’équation première et
deuxième du premier système , vérifie ces équations (ici les nombres sont x= 2
et y = 5 ) cela veut dire que le nombre "« x-2y est égal au nombre 4
, ou le nombre 7x est égal au nombre 2y +4 , ou enfin x =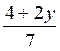
;
donc l’équation première du second système est vérifiée.
Les nombres « x »x et « y »
vérifie par hypothèse la deuxième équation du premier système ; mais dans
cette équation le nombre « x » est identique au nombre ;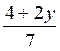
donc cette équation , dans laquelle on remplace
x par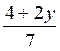 , doit être vérifiée , c’est précisément la
deuxième équation du second système .
Donc les deux équations du deuxième système sont
vérifiées.
2°)
Toute solution du système II est solution d système I.
Supposons que deux nombres mis l’un à la place se
« x » , l’autre à la place de « y » dans la première et la
seconde équations du second système vérifient ces équations ; cela veut
dire que le nombre « x » est identique au nombre 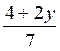ou 7x est identique à 2y +4 , ou enfin 7x-2y
est identique à 4 , donc la première
équation du premier système est vérifiée
pour ces valeurs de « x » et de « y ».Le nombre
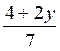« x » étant identique à par le nombre « x » , dans la deuxième équation du second système , qui ,
par hypothèse , est vérifiée pour les valeurs de « x » et de
« y » ; on a alors l’équation 3x+8y = 46 , qui est vérifiée ,
mais c’est la deuxième équation du premier système ; donc les deux
équations du premier système sont
vérifiées pour ces valeurs de »x » et de « y » et le
principe est établi.
La démonstration
se ferait de la même manière si
on avait un système de plus de deux équations simultanées.
Solution
du système ou « racines » :
On appelle « solution du système » les nombres qui vérifient à la fois toutes
les équations du système.
|
Par exemple ,
le système :
admet la solution x = 2 ;
y =1 il suffit de
vérifier ! ! ! !
que 2 + 1 = 3 ; et que 2
+ 3 fois1 =5 |
TRAVAUX AUTO
FORMATIFS :
CONTROLE :
1°)
Qu’est ce qu’un système de deux équations simultanées.
2°)
Montrer un modèle mathématique.
EVALUATION
A
partir du système suivant , trouver un second système
équivalent.
