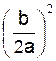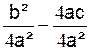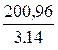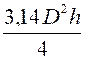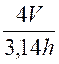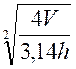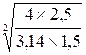|
Auteur :
Warmé Raymond |
|
|||||||||||
|
Nomenclature 1 |
||||||||||||
|
Factoriser la
forme « ax2+b x +c » |
||||||||||||
|
Information sur le
"second degré" |
||||||||||||
|
ENVIRONNEMENT du
dossier: |
|
|||||||||||
|
Objectif précédent 2°) Approche pédagogique : présentation de la forme
canonique à partir d’un exemple. |
||||||||||||
|
|
|
|
|
|||||||||
|
Cours : FORME
CANONIQUE de la fonction et factorisation du
polynôme du second degré I ) Forme canonique de la fonction polynôme du second degré. II )
« Factorisation » de
la fonction polynôme du 2ème degré « ax2 + bx + c » |
|
|||||||||||
|
TEST |
COURS |
|
||||||||||
COURS
I ) Forme canonique
de la fonction polynôme du second degré.
|
Voir factorisation |
||
|
Soit l’
équation : a x2 + b x + c |
||
|
|
Soit f (x)
= ax2 + b x
+ c ; a ¹ 0 On peut écrire ax2 + b x
+ c = a ( x
2 + x2 + de
( x + ainsi : ( x + on obtenons : ( x + on peut
remplacer : [x2 + d’où soit f (x) = a [x2 + (
A ) regroupons :
quelque soit la valeur de
« x » appartenant à l’ensemble des nombres réels : ax2 + b x
+ c = a[( x
+ la forme obtenue est
appelée « forme canonique »
de la fonction polynôme du second degré . |
|
Etude d’ exemples :
Exemple N°1
Soit la fonction f définie par : f(x) = x2
– 4x + 10
En remarquant que « x2
– 4x » est le début du développement de ( x – 2 )2
( x – 2 )2 = x2 – 4x + 4
On déduit
que quelque soit « x » appartenant à l’ensemble des réels :
x2
– 4x = ( x – 2 )2 – 4
soit x2 – 4x + 10 = ( x – 2 )2
– 4 +10
x2 – 4x + 10
= ( x – 2 )2 + 6
Exemple N°2
Soit la fonction f définie par : f(x) = 3x2
– 2x + 4
quelque soit « x » appartenant à l’ensemble des réels :
3x2
– 2x + 4 = 3 (![]() x2 –
x2 – ![]() x +
x + ![]() )
)
3x2
– 2x + 4 = 3 (x2 – ![]() x +
x + ![]() )
)
en remarquant que « x2 – ![]() x » contient les deux premiers termes du développement
d’un carré , on obtient :
x » contient les deux premiers termes du développement
d’un carré , on obtient :
x2
– ![]() x = (x –
x = (x – ![]() )2 -
)2 - ![]()
d’où x2 – ![]() x +
x + ![]() = (x –
= (x – ![]() )2 -
)2 - ![]() +
+ ![]() = (x –
= (x – ![]() )2 +
)2 + ![]()
donc : quelque soit « x »
appartenant à l’ensemble des réels :
3x2
– 2x + 4 = 3 [(x – ![]() )2 +
)2 + ![]() ]
]
exemple
N°3 :
Soit la fonction f définie par : f(x) = 2x2
– 7x - 4
quelque soit « x » appartenant à l’ensemble des réels :
2x2 – 7x - 4 = 2
(x2 – ![]() x - 2)
x - 2)
x2 – ![]() x = (x2 –
x = (x2 – ![]() )2 -
)2 -![]()
d’où
x2 – ![]() x - 2 =(x2 –
x - 2 =(x2 – ![]() )2 -
)2 -![]() -2 = (x2 –
-2 = (x2 – ![]() )2 -
)2 -![]()
donc :
quelque soit « x » appartenant à l’ensemble des réels :
2x2
– 7x - 4 = 2 [(x2 – ![]() )2 -
)2 -![]() ]
]
II ) « Factorisation » de la fonction polynôme du 2ème
degré « ax2 + bx + c »:
De « ax2 + bx + c »
on a : a[( x + ![]() )2 -
)2 -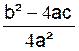 ]
]
la forme
obtenue a[( x + ![]() )2 -
] est appelée « forme canonique » de la fonction
polynôme du second degré .
)2 -
] est appelée « forme canonique » de la fonction
polynôme du second degré .
Nous
posons : ![]() = b2 – 4ac
= b2 – 4ac
Le nombre réel « b2 – 4ac » est appelé « discriminant » de la
fonction polynôme f.
Ainsi :
ax2 + bx + c = a [( x + ![]() )2 -
)2 -![]() ]
]
![]() désignant
la racine carrée positive de
désignant
la racine carrée positive de ![]() , on obtient :
, on obtient :

![]() =
= 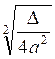 =
= 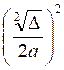 (pour cette transformation voir puissance d’un rationnel )
(pour cette transformation voir puissance d’un rationnel )
on
en déduit :
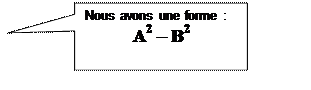 f(x) = a[( x +
f(x) = a[( x + ![]() )2 -
)2 -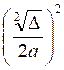 ]
]
|
nous avons une forme d’une identité
remarquable : A2 – B2
= (A+B) (A-B) ou
« A » vaut « x +
|
|
D’où f(x) = a [x
+ ![]() +
+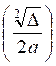 ] [x +
] [x + ![]() -
-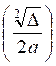 ]
]
Posons x’ = 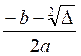 et x’’ =
et x’’ =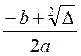
On obtient alors : ax2 + bx + c =
a ( x – x’ ) ( x –x’’)
2ème cas : ![]() = 0
= 0
D’où f(x) =
a [x + ![]() + 0] [x +
+ 0] [x + ![]() - 0]
- 0]
D’où f(x) = a [x
+ ![]() ] [x +
] [x +
![]() ]
]
D’où f(x) = a [x
+ ![]() ]2
]2
3ième cas : ![]() < 0 :
< 0 :
Dans ce cas aucune factorisation n’est possible
|
La factorisation de f(x) = ax2 + bx + c , dépendra du
discriminant : 1er cas : Avec x’ = 2ème cas : D’où ax2 + bx + c
se factorisera en f(x) = a [x +
3ième cas : |
Donner la forme canonique des trinômes
suivants :
N°1
Soit la fonction f définie par : f(x) = x2
– 4x + 10
En remarquant que « x2
– 4x » est le début du développement de ( x – 2 )2
( x – 2 )2 = x2 – 4x + 4
On déduit
que quelque soit « x » appartenant à
l’ensemble des réels :
x2 – 4x = ( x – 2 )2
– 4
soit x2 – 4x +
10 = ( x – 2 )2
– 4 +10
x2 – 4x + 10
= ( x – 2 )2 + 6
N°2
Soit la fonction f définie par : f(x) = 3x2
– 2x + 4
quelque soit « x » appartenant à l’ensemble des réels :
3x2 – 2x + 4 = 3 (![]() x2 –
x2 – ![]() x +
x + ![]() )
)
3x2 – 2x + 4 = 3
(x2 – ![]() x +
x + ![]() )
)
en remarquant que « x2 – ![]() x » contient les deux premiers termes du développement
d’un carré , on obtient :
x » contient les deux premiers termes du développement
d’un carré , on obtient :
x2 – ![]() x = (x –
x = (x – ![]() )2 -
)2 - ![]()
d’où x2 – ![]() x +
x + ![]() = (x –
= (x – ![]() )2 -
)2 - ![]() +
+ ![]() = (x –
= (x – ![]() )2 +
)2 + ![]()
donc : quelque soit « x » appartenant à l’ensemble des réels :
3x2 – 2x + 4 = 3
[(x – ![]() )2 +
)2 + ![]() ]
]
N°3 :
Soit la fonction f définie par : f(x) = 2x2
– 7x - 4
quelque soit « x » appartenant à l’ensemble des réels :
2x2 – 7x - 4 = 2
(x2 – ![]() x - 2)
x - 2)
x2 – ![]() x = (x2 –
x = (x2 – ![]() )2 -
)2 -![]()
d’où x2 – ![]() x - 2 =(x2 –
x - 2 =(x2 – ![]() )2 -
)2 -![]() -2 = (x2 –
-2 = (x2 – ![]() )2 -
)2 -![]()
donc : quelque soit « x » appartenant à
l’ensemble des réels :
2x2 – 7x - 4 = 2
[(x2 – ![]() )2 -
)2 -![]() ]
]
N°5 : x2
– 16x + 39
N°6 : 3x2 + 8x
+ 4
N°7 :
10x2 – 49x + 51
N° 8 :
6 x2 – 17x - 45
Factorisation de la fonction
polynôme du second degré:
Donner la forme mathématique du discriminant :
|
En résumé à réciter : La factorisation de f(x) = ax2 + bx + c , dépendra du
discriminant : 1er
cas : Avec x’ = 2ème cas : D’où ax2 + bx + c se factorisera en f(x) = a [x + 3ième
cas : |
EVALUATION
AIRE
d' un CARRE:
|
A = c 2 |
A = aire |
c = longueur d' un coté |
Problème
1:
Calculer le coté d'un carré de
|
225 cm2 = c 2 |
D'ou c = |
C = + ou -
Conclusion : le coté du carré vaut La solution négative ne peut convenir. |
Problème
2
Calculer le rayon d'un disque dont on connaît son
aire:
|
A = 200,96 cm2 |
A = 3,14 R2 |
|
Donc 200,
96 = 3,14 r2 |
Après transformation R2 = 64 |
|
R = |
R = |
Problème
3
Quel diamètre convient-il de donner à un cylindre de
|
25 hectolitres |
25 |
25 00 décimètres cubes |
2 , |
|
Le volume d'un cylindre: V = |
|
|
4V = 3,14 D2h |
D2 = |
|
|
D = |
|
|
D = |
|
|
|
Le mouvement uniformément varié
|
V = vo + a t |
"V " est la vitesse au temps
"t" "V o " est la vitesse
initiale "e"
désigne l' espace parcouru "a" désigne l' accélération du mouvement "t"
temps mis |
|
e = vot + |
"V o " est la vitesse
initiale "e"
désigne l' espace parcouru "a" désigne l' accélération du mouvement "t"
temps mis |
|
Si le corps part du repos : vo = 0
; alors les formules
deviennent: V = vo + a t devient V
= 0 + a t ; e = vot + |
V = a t e = + |
|
|
|
Problème
1:
Au départ d'une gare un train met 40 secondes pour
atteindre sa vitesse uniforme de
On demande :
L' accélération du mouvement de départ.
L'espace parcouru quand il atteint sa vitesse
normale;
Le temps mis pour s'arrêter;
La distance de la gare d'arrivée à laquelle le mécanicien
doit cesser l'admission de vapeur.
1° v = at , d'où a![]()
v =
ou 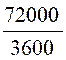 =
=
a = ![]() = 0,50m par seconde
= 0,50m par seconde
2° e = +![]() a t2 ; e = +
a t2 ; e = +![]() 0,50
0,50 ![]() 402 =
402 =
3°) V = vo
+ a t de cette formule nous tirons : t = 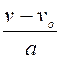
mais v =
0 correspond à l' arrêt ; vo = vitesse initiale
t = 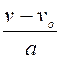 ; t =
; t = 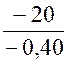 ; t = 50 secondes
; t = 50 secondes
4°) e = vot +![]() a t2 ; e = 20
a t2 ; e = 20![]() 50 +
50 + ![]()
![]() (-0,40)
(-0,40) ![]() 502
502
e = 1000-500
=