|
DOC : Formation Individualisée |
DOC : Elève. |
|
DOSSIER :
Matière : MATHEMATIQUE |
Information
« TRAVAUX » :Cliquer sur le mot !. |
|
OBJECTIFS : - Savoir
résoudre l’équation du second
degré avec S et P |
I ) Pré requis:
|
1- |
|
II ) ENVIRONNEMENT du dossier :
|
Dossier précédent « étude ……. : |
Dossier suivant : |
Info : Tableau synoptique
:i Info :
Retour vers la liste des cours sur
le second degré « équations » |
|
|
|
|
|
|
LE SECOND DEGRE : Somme et produit des solutions :
Relations entre les solutions et les coefficients
du second degré.
IV) INFORMATIONS
« formation leçon » :
|
Travaux auto - formation. |
|
Corrigé des travaux
auto - formation. |
||||
|
Corrigé |
||||||
V ) DEVOIRS ( écrits):
à compléter
|
Devoir diagnostique L tests. |
|
|
Devoir Auto
- formatif
(intégré au cours) |
|
|
Devoir
Formatif « Contrôle :
savoir » ; (remédiation) |
|
|
|
|
|
Devoir sommatif. |
|
|
Devoir certificatif : (remédiation) |
|
* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .
|
Titre |
|
|
|
LE SECOND DEGRE :
Les relations entre S et P
et « x’ » et
« x’’ » |
Relations
entre les solutions (racines) et les
coefficients de l’équation du second degré
Les solutions
de l’équation a x² + b x + c
étant : x’ = 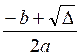 ; x’’ =
; x’’ = 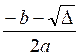
Calculons
la somme S = x ‘ + x ‘’ et
le produit P =
x’ x’’
1°) Somme « S » = x ‘ +
x ‘’
S =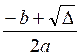 +
+ 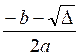 =
= 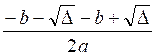 =
=
S = ![]() = -
= -![]()
Conclusion : la somme des racines d’une équation du second
degré est égale à -![]()
2°)
Calcul du produit « P » = x’ x’’
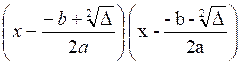 =
= 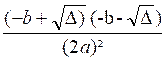
( Le numérateur est de la forme (A+B) ( A -B) qui est égal à A² - B²)
le
numérateur est le produit de la somme des termes « -b » et «![]() » par leur différence, il est donc égal à la différence
de leurs carrés,soit b² - ” et :
» par leur différence, il est donc égal à la différence
de leurs carrés,soit b² - ” et :
P = 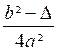
Remplaçons ” par sa valeur ( b²-
4ac) le produit devient :
P = 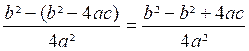
P = ![]() soit en divisant les
deux termes par « 4a » P =
soit en divisant les
deux termes par « 4a » P = ![]()
Conclusion : le produits des solutions (racines) d’une
équation du second degré est égal à
« ![]() »
»
Nous
pouvons écrire que :
a x² + b x + c ; on met en facteur « a », on obtient
« a ( x² +![]() x +
x +![]() ) »
) »
ou
a ( x² - S x + P ) = 0
APPLICATIONS :
A-
Calcul mental des solutions de certaines équations :
Soit l’équation x² - 6 x + 8 = 0
|
x² - 6 x + 8 = 0 |
a ( x² - S x + P ) = 0 |
|
a=
1 ; S = 6 ; P = 8 |
On
identifie : a ; S ; P |
|
Le
produit des solutions est égal à 8 , la somme est
égale à 6 , on devine facilement que les nombres 2 et 4 réalisent ces
conditions, ce sont les solutions de l’équation. |
|
B- Reconnaître les signes des solutions d’une
équation du second degré sans les avoirs calculées.
Exemple : 1
x² - 8 x + 15 = 0
|
a = +1 , b = -8 ,c = +15 |
Commentaire : |
|
” = 64 - 60
= +4 donc
> 0 |
2
solutions distinctes |
|
P = |
Elles
ont le même signe |
|
S = |
Elles
sont positives |
En
effet on trouve x’ = 5 ; x’’ = 3
Exemple :2 4 x² + 11 x + 6 = 0
|
a =
+ 4 ; b = + 11 ; c = +6 |
Commentaire : |
|
” = 121 - 96
= +25 donc
> 0 |
2
solutions distinctes |
|
P = |
Elles
ont le même signe |
|
S = |
Elles
sont négatives |
En
effet on trouve x’ = - 3/4 ; x ‘’
= - 2
Exemple :
3 2 x² - 5 x - 3 = 0
|
a =
+ 2 ; b = -5 ; c = - 3 |
Commentaire : |
|
” = 25 + 24
= + 49 donc
> 0 |
2
solutions distinctes |
|
P = |
Elles
sont de signes contraires La
plus grande en valeur |
|
S = |
Absolue
est positive |
En
effet on trouve x’ = 3
; x ‘’ = - 1 / 2
Exemple :
4 4 x² + 2 5 x - 21 = 0
|
a =
+ 4 ; b = + 25 ; c = - 21 |
Commentaire : |
|
” = 625 + 336
= + 961 donc
> 0 |
2 solutions
distinctes |
|
P = |
Elles
sont de signes contraires La
plus grande en valeur |
|
S = |
Absolue
est négative |
En
effet on trouve x’ = 3 /4 ; x ‘’ = - 7
Tableau
résumé de la discussion de l’équation du second degré.
|
Cas :
avec P = |
Condition : si |
Alors : |
|
il y a certainement 2 solutions de signes contraires. |
|
La plus
grande en valeur absolue est positive. |
|
|
La
plus grande en valeur absolue est négative. |
|
|
|
Les
deux solutions sont opposées. |
|
avec P = |
Valeur
de ” |
Valeurs
des solutions |
Commentaires :
|
|
il faut
former le ” |
” > 0 Il y a deux solutions |
|
Les deux
solutions sont positives. |
|
|
Les
deux solutions sont négatives. |
||
|
” = 0 Il y a une solution |
|
Il y
a deux solutions égales ayant pour valeur commune= |
|
|
” < 0 |
Il n’ y a pas de solution calculable. |
||
|
|
Il y
a une solution nulle, l’autre étant
égale à |
C
- Trouver deux nombres connaissant leur
somme (S) et leur produit (P):
Divisons
par « a » les termes de l’équation a x² + b
x + c (1)
, on
obtient « x² +![]() x +
x +![]() »
»
Or ![]() = - S
et
= - S
et ![]() = P
= P
Et
l’ équation (1) peut s’écrire x² - S
x + P = 0 (2)
Réciproquement,
les solutions de l’équation (2) seront les deux nombres ayant pour somme
« S » et pour produit « P ».
On peut énoncé :
Pour que deux nombres « x »
et « y » aient pour somme « S » et pour produit « P » , il faut et il suffit qu’ils soient racines de l’équation en
« z ».
|
|
z ² - S z + P = 0 |
|
La
condition d’existence de « x » et « y » est S² - 4P "e 0
Exemple : trouver deux nombres ayant pour somme 25 et pour produit 144
Ces
deux nombres sont les solutions de l’équation
z² - 25 z + 144
a = +1 ; b = - 25 ; c = + 144
Calcul
de ” : ( b² - 4ac ) = 625 -
576 = 49
Calcul
de ![]() :
: ![]() = 7
= 7
x
= 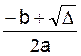 soit x
=
soit x
= 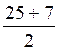 = 16
= 16
et y
= 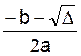 soit y
=
soit y
= 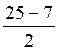 = 9
= 9
Les
deux nombres demandés sont 16
et 9
Remarques
relatives à ce problème :
Les
deux nombres ayant pour somme « S »
et pour produit
« P » existent si le discriminant
de l’équation (2) est positif ou nul.
S² - 4P = 0
Soit S²
= 4P ; 4P = S² ; P =
![]()
La
plus grande valeur possible de P est donc ![]() et dans ce cas l’équation
( 2) a deux solutions égales.
et dans ce cas l’équation
( 2) a deux solutions égales.
1°) Remarque arithmétique :
Si la somme de deux nombres variables est fixe , le
produit de ces deux nombres est maximum quand ils sont égaux.
2°) Remarque géométrique : de tous les rectangles dont le demi-
périmètre est donné, celui dont l’aire
est maximum , est le carré.
On
peut aussi écrire S² = 4P et en supposant S et P positifs
S
= ![]() ; S = 2
; S = 2![]()
La plus petite valeur de S est
donc 2![]() et dans ce cas
l’équation (2) a deux solutions égales. On en déduit les deux remarques :
et dans ce cas
l’équation (2) a deux solutions égales. On en déduit les deux remarques :
1°) Remarque arithmétique :
Si la somme de deux nombres positifs variables est fixe ,
la somme de ces deux nombres est minimum quand ils sont égaux.
2°) Remarque géométrique : Si « x »
et « y » sont les dimensions
d’un rectangle , leur somme « S » est le demi périmètre et leur
produit « P » est l’aire du rectangle . On en conclut :
1°) De tous les rectangles qui ont une aire donnée , celui qui ale plus petit périmètre est le carré .
2°) De tous les rectangles qui ont un périmètre
donné, celui qui a la plus grande surface est le carré.
D)
Autres applications .
Les
expressions x’ + x’’ = -![]() et x’ x’’ =
et x’ x’’ = ![]()
Sont
utilisées chaque fois qu’il s’agit de résoudre un problème comportant une relation entre les solutions
x’ et x’’ ou leurs inverses, ou leurs
puissances, etc. C’est encore en éliminant le paramètre entre la somme et le
produit des solutions d’une équation du second degré à paramètre, qu’on
démontre que celles - ci satisfont à une
relation indépendante de ce paramètre.
L’intérêt
pratique de ces questions étant rigoureusement « nul » , nous laisserons de côté, renvoyant à un autre « dossier » les lecteurs qui
ayant en vue la préparation d’un examen seraient obligés de s’y
« intéresser ».
|
Leçon |
Titre (niveau IV) |
|
N° |
TRAVAUX d ’ AUTO - FORMATION
sur le second degré :
Somme et Produit |
EVALUATION
Former
les équations du second degré ayant pour solutions :
|
1.
|
-
2/5 et 8 |
|
|
2.
|
2/4
et 6 |
|
|
3.
|
-7
et - 1/2 |
|
|
4.
|
a+b et
a -b |
|
|
5.
|
1/ ( a+b) et 1 / (a - b) |
|
|
6.
|
1 +
2 |
|
|
7.
|
( |
|
|
8.
|
ab
et a/b |
|
|
9.
|
(ab)
/ ( a+b) et (ab) / (a - b) |
|
Problèmes :
1°)
Etant donné l’équation x² + p x + q = 0 déterminer p et q de façon que les
solutions de l’équation soient égales à p et à q.
2°)Soit AH le hauteur du triangle ABC relative à la base BC .
ON connaît AB = 5 cm ; AC = 4 cm.
On sait que de plus BH fois DH = 135 / 16 . Calculer B C .
3°)
Trouver deux nombres tels que leur différence soit 5 et leur produit 60.
4°)leur différence -
10 et leur produit - 21
4°) Calculer les côtés d’un rectangle dont le périmètre est 26
mètres et la surface 40 mètres carrés.