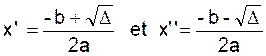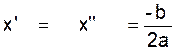|
|
|
|
|
|
2°)A voir : Etudes de fonctions :
le second degré. |
Info cours de niveau IV : sur « la
dérivée » |
||
|
|
|
|
|
DOSSIER:ETUDES DE FONCTIONS : La fonction
« trinôme » du second degré.
Chapitres :
I)
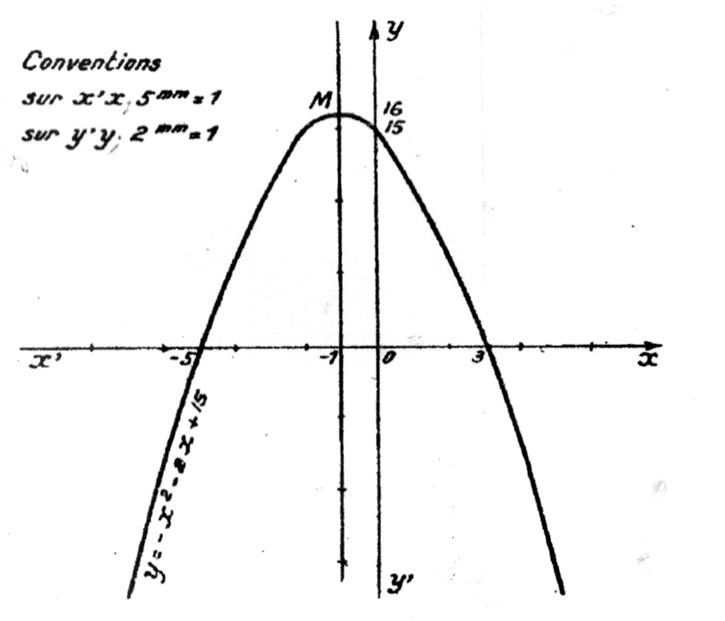
Exemple : Etude de
la fonction trinôme : y = - x² - 2x + 15
II)
Généralisation.
III)
Exemple d’ exercice : lancement d’un projectile.
|
Interdisciplinarité |
|
I ) Etude de la fonction trinôme ![]()
|
A) Recherche des valeurs remarquables : |
||
|
|
(voir la représentation graphique avec la calculatrice graphique
) |
|
|
1°) Domaine de définition : |
||
|
Ou recherche des valeurs
« exclues » de « x » ? La fonction n’est ni rationnelle ni irrationnelle , donc toutes les valeurs de « x »
conviennent. |
1°) Cette fonction est définie pour
toute valeur de « x ». |
|
|
|
|
|
|
2°)
Calcul de « y » pour
« x= 0 » cela
revient à résoudre l’équation de la forme : 0 = a
0 ² + 0 x + c |
||
|
|
2°)
si « x= 0 » y = - 0² - 2 fois 0 + 15 ; d’ où y = +15 |
|
|
3°) Calcul
pour y = 0 cela
revient à résoudre l’équation de la forme : 0 = a
x² + b x + c |
||
|
|
si
« y = 0 » l’équation 0 = a x² + b x + c s’écrit : 0 = - x² -
2x + 15 l’équation admet 2 solutions : x’ = +3 et x’’ = - 5 |
|
|
4°) Valeur des limites : aucun
intervalle d’étude n’étant fixé , ( borne mini et maxi de « x » ) on
étudie ce que peut être les valeurs de « y » si « x » tend + ∞
et ou - ∞ |
||
|
|
La fonction « y » étant
équivalente à son terme du plus haut degré « -x² » a pour
valeur : - ∞ |
|
|
B) calcul de
la dérivée :
« y ’ » |
|
|
Commentaire : (on suppose que l’on ne
trace pas la courbe ) Recherche s’il existe un minima ou un maxi
par le calcul de la dérivée. « y’ », par le calcul . ( la réponse se trouve
lorsque l’on analyse le tracé). |
|
|
1°) La dérivée de « ax² + bx + c » et
de la forme « 2ax + b » |
La dérivée de « |
|
2°)
Cas ou « y ‘ = 0 » ; On
résout l’équation de la forme : «
2ax + b = 0 » |
Y’
= 0 si « Soit
- 2x = 2 ; x = ( - 2 /
2) ; |
|
3°)
Est ce un minima ou un
maxima ? on
calcule la dérivée seconde est on étudie le signe . « y’’ = 2a » ( y’’ = dérivée
de « y’ = 2ax + b » ) |
La dérivée de « Donc on en conclut que l’annulation de
« y’ » correspond à un maxima pour « y » |
|
4°)
coordonnées de ce maxima ou minima. On
remplace « x = - 1 » dans l’expression « y = - 2 x² - 2x +15 » |
Coordonnées du maxima :
« y = - 2 ( -1)² - 2 (
-1) + 15 »
« y = + 16 » |
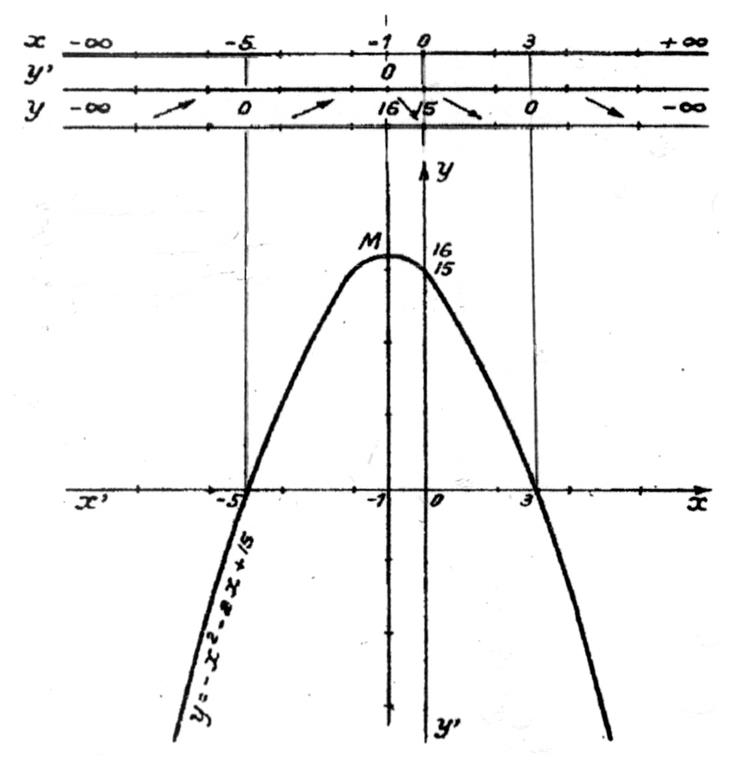
C ) Il reste à mettre toutes ces valeurs dans un
tableau :
|
|
|
Ce tableau
porte le nom de « tableau
de variation ».
Remarque : connaissant ces valeurs
particulières, on peut tracer la courbe d’équation « y = - 2 x² - 2x
+15 ».
Plus on placera de points (les coordonnées de ces points sont
obtenu par calcul qui pour des valeurs de « x » fixées on trouvera la
valeur correspondante de « y », plus le tracé de la courbe sera précis et proche de
la réalité)
|
|
On
résumera l’étude : à un tableau et le tracé de la
courbe :
(On peut faire correspondre le tableau et le
tracé)
|
|
GENERALISATION : ETUDE
DE LA FONCTION de la forme : « y = a x² + b x + c »
On a remarqué que « y ’’ = 2a ». Il
s’ensuit que :
► si
« a » est positif , la courbe entière ,
tourne sa concavité vers les « y » positifs et l’annulation de
« y’ » correspond à un minimum pour la fonction.
► si
« a » est négatif , la courbe entière ,
tourne sa concavité vers les « y » négatifs et l’annulation de
« y’ » correspond à un maximum pour la fonction.
Nous envisagerons dans cette généralisation,
ces deux cas :
( 1er cas où a
>0 ; 2ème cas où
a<0)
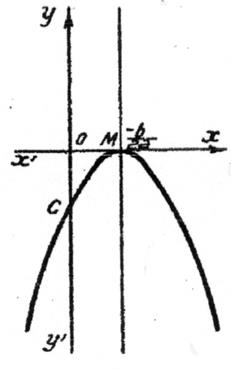
1er cas : a > 0
A)
calcul
des valeurs remarquables :
► on pose « x = 0 ; on en déduit :
« y = c » ; l’ordonnée « c » détermine
l’intersection de la courbe représentative avec l’axe des « y ».
► « x = ![]() » ;
« y » étant équivalent à son terme du plus haut degré « a
x² » a pour valeur « + ∞ »
» ;
« y » étant équivalent à son terme du plus haut degré « a
x² » a pour valeur « + ∞ »
· Dans certains l’étude est limitée dans un
intervalle donné , les valeurs « x mini» et
x maxi » vont donné des valeurs « y »
particulières.
►on pose
« y = 0 » ; c’est à
dire que l’on doit résoudre « a x²
+ b x + c = 0 »
On calcule le discriminant : ∆ = b² -
Alors on rencontre trois cas :
|
Valeurs du ∆ |
Solutions |
Conséquences graphiques |
|
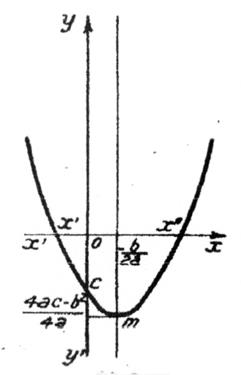
∆ > 0 |
2 solutions distinctes :
|
►La courbe représentative coupe l’axe des « x » en deux
points distinctes |
|
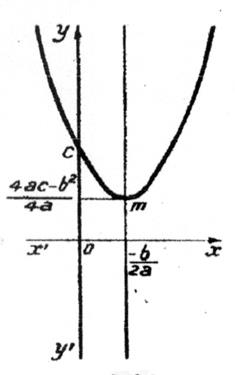
∆
= 0 |
2 solutions égales :
|
►La courbe représentative est tangente à l’axe des
« x ». |
|
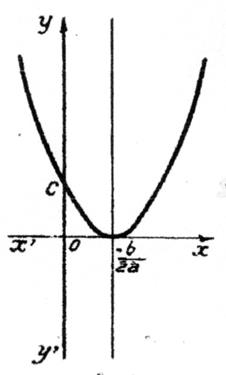
∆
< 0 |
Pas de solution |
► la courbe représentative est située toute entière
au dessus de l’axe des « x ». |
B ) calcul
de « y ’ »
« y ‘ =
y ’ = 0 si 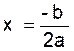
La fonction passe par un minimum pour 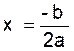 , ce minimum a pour
valeur :
, ce minimum a pour
valeur :
Calcul de « y » avec 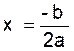 :
:
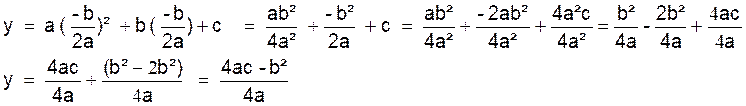
ce minimum a pour valeur : 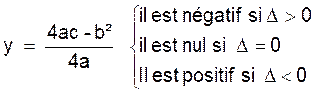
Ci dessous l’allure des courbes représentative correspondant au différents cas :
( « ∆ » lire « delta »)
|
Si ∆
> 0 |
Si ∆
= 0 |
Si ∆
< 0 |
|
|
|
|
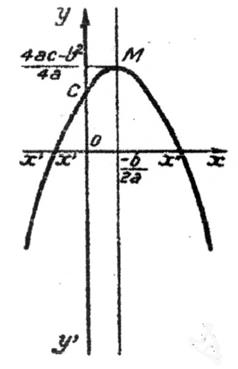
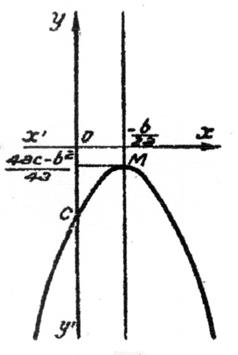
2ème cas :
a < 0
L’étude de ce cas est analogue à la
précédente. Cependant :il y a une différence au point (2) et
(4)
(1) ► on pose « x = 0 ; on en
déduit : « y =
c ».
( 2) ► « x = ![]() » ;
« y » étant équivalent à son terme du plus haut degré « a
x² » a pour valeur « - ∞ »
» ;
« y » étant équivalent à son terme du plus haut degré « a
x² » a pour valeur « - ∞ »
(3) ►on pose « y = 0 » ; c’est à dire que l’on doit résoudre « a x² + b x + c
= 0 »
(4) ►On calcule le
discriminant : ∆ = b² -
L’étude de ce cas est analogue à la précédente
. Cependant : pour
(5) ► la
fonction passe par un maximum, ce
maximum à pour valeur :
ce minimum a pour valeur : 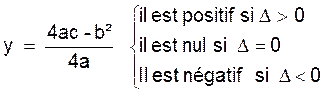
Ci dessous l’allure des courbes représentative correspondant au différents cas :
( « ∆ » lire « delta »)
|
Si ∆
> 0 |
Si ∆
= 0 |
Si ∆
< 0 |
|
|
|
|
La courbe « y = a x² + b x + c » est
une parabole
dont l’axe de symétrie est la parallèle à l’axe des « y » (axe des
ordonnées) menée par l’abscisse 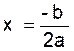 :
:
Exercice :
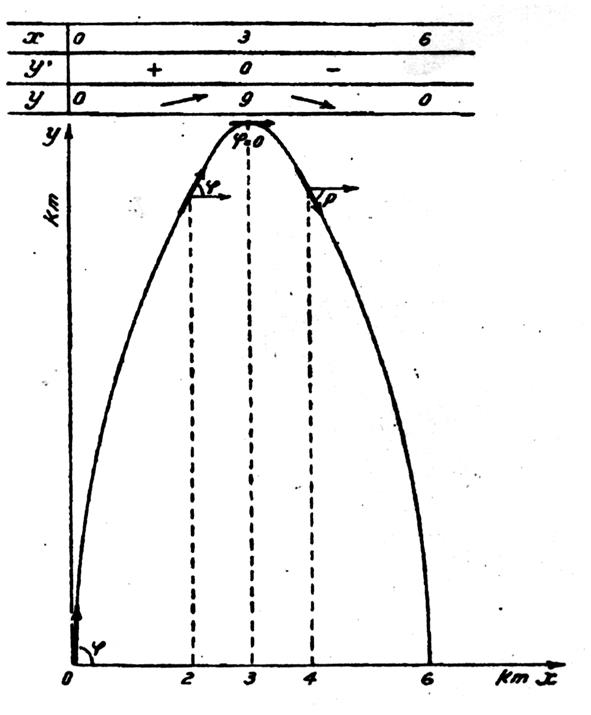
Un canon lance un projectile dont la trajectoire parabolique a pour équation
« y = - x² + 6x . En représentant le kilomètre par
1°) à la sortie du canon
2°) à une distance de
3°) à une distance de
En quels points de la trajectoire :
1°) le projectile se déplace - t- il horizontalement ?
2°) Le projectile fait -il un angle de 45°
avec l’horizontale ?
Solution :
Domaine de définition : la fonction y = -
x² + 6 x est étudiée dans l’intervalle compris entre « x = 0 » et la valeur positive de « x » qui
annule « y » soit « x =
6 ».
La dérivée « y’ » est égale à « - 2x + 6 » , elle s’annule pour
« x = 3 », la hauteur correspondant atteint par le projectile
est de
Nous avons vu que la dérivée dans l’expression
de laquelle nous remplaçons la variable par une valeur « a » mesure la pente de la tangente à la courbe
représentative au point d’abscisse « a » : donc
1°) si x = 0
, y’ = 6 , tan
φ = 6 ; φ # 80°
2 °) si x = 2
, y’ = 2 , tan φ = 2;
φ # 64°
3°) si x = 4
, y’ = -2 ,
tan φ = -2 ; φ
# - 64 °
lorsque le projectile se déplace
horizontalement « φ =
0 » ; tan φ = 0 ; y’
= 0 . Ce point est donc le sommet de la trajectoire.
Si l’inclinaison est de 45° , tan
φ = +1 , suivant que le projectile monte ou descend. On a
donc :
- 2x + 6 =
± 1 ; 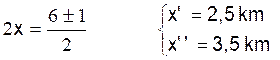
Tableau et représentation graphique ::
|
|