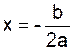|
Ce cours est la
suite de l’objectif n°«3°) Etude d’une
fonction trinôme. »
|
|
|
Rappel : Etude graphique d’une fonction. |
|
|
Index |
Objectif
précédent 1°) Plan
concernant l’étude d’une fonction. |
|
DOSSIER: ETUDES DE FONCTIONS :
Etude du signe du trinôme du second degré. Par
la méthode graphique.
I)
Cas 1 : « b² - 4 ac < 0 »
II)
Cas 2 : « b² - 4 ac = 0 »
III)
Cas 3 : « b² - 4 ac > 0 »
IV ) Règle .
|
|
|
Devoir Contrôle |
Interdisciplinarité
|
|
Corrigé Contrôle |
Corrigé évaluation |
L’étude du signe est
subordonnée au calcul du discriminant :
∆ = b² - 4 ac
et à son résultat : ∆ > 0 ;ou ∆ = 0 ; et ou ∆ < 0
I ) Cas : b² - 4 ac
< 0
Nous savons déjà (info ++)
que si le discriminant est négatif , la courbe ne
coupe pas l’axe des abscisses.
L’allure de la courbe
dépend du signe de « a » dans l’équation « a x² + b x
+c » ; « a » pouvant être positif ou négatif.
|
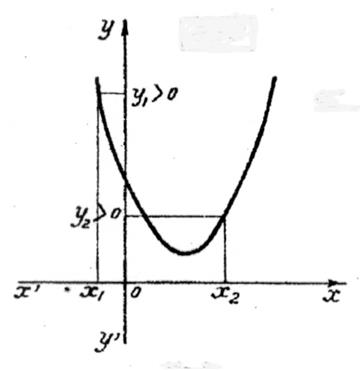
Si b² - 4 ac est négatif et si « a >0 » : On remarque que tout point de la courbe a
une ordonnée positive , c’est à dire du signe de
« a » |
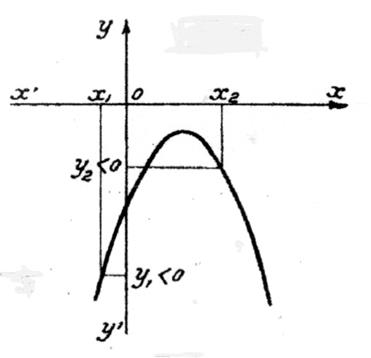
Si b² - 4 ac est négatif et si « a < 0 » On remarque que tout point de la courbe a
une ordonnée négative , c’est à dire du signe de
« a » |
|
|
|
L’ordonnée
« y » correspondant à
n’importe quelle , abscisse « x » est
du signe de « a » .
Règle : si le discriminant est négatif , le trinôme « a x² + b x + c » a le
signe de « a » pour n’importe quelle valeur de « x ».
2ème
cas : b² - 4 ac = 0
|
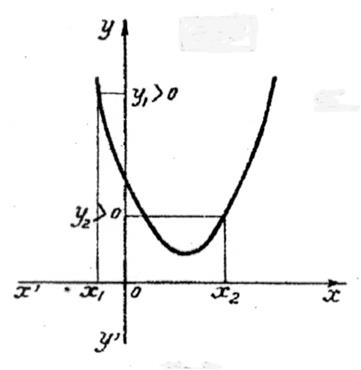
Si
b² - 4 ac
est = 0 et si
« a > 0 », l’allure de la représentation graphique de la
courbe sera : |
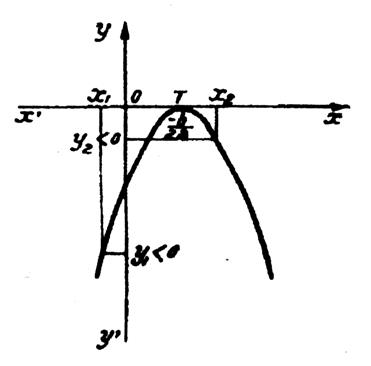
Si
b² - 4 ac
est négatif et si « a < 0 » ,
l’allure de la représentation graphique de la courbe sera : |
|
|
|
|
Si
b² - 4 ac
est = 0 et si
« a > 0 »Tous les points de la courbe ont une ordonnée positive , c’est à dire du signe de « a » , sauf
pour le point de tangence dont l’ordonnée est nulle. |
Tous les points de la courbe ont une
ordonnée négative , c’est à dire du signe de
« a » , sauf pour le point de tangence dont l’ordonnée est nulle. |
|
L’ordonnée « y »
, correspondant à n’importe quelle abscisse « x » , est du
signe de « a » sauf , l’ordonnée du point de tangence (tangent à
l’axe des abscisses) qui est nulle , ce point ayant pour abscisse « On en tire
la règle suivante : Si le discriminant est nul , le trinôme du
second degré « y = a x² + b x + c » a le signe de « a »
pour n’importe quelle valeur de « x » , sauf, pour « Valeur de la solution double de l’équation
« a x² + b x + c = 0» , le trinôme est
alors nul. |
|
2ème
cas : b² -
4 ac > 0
|
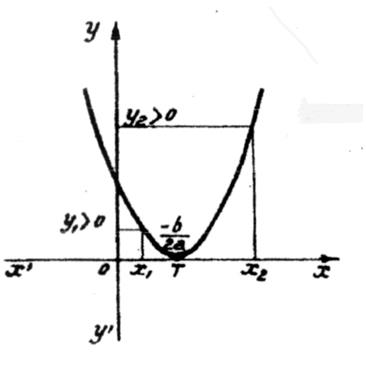
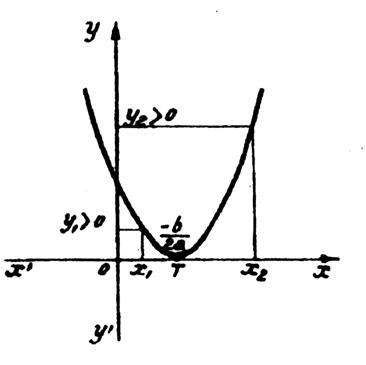
Si b² - 4 ac est positif et si « a > 0 », l’allure de la représentation
graphique de la courbe sera : |
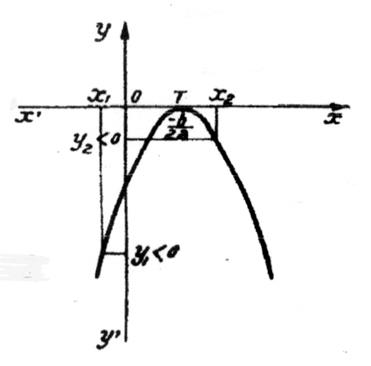
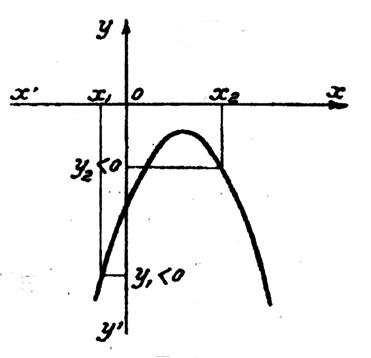
Si b² - 4 ac est positif et si « a <
0 », l’allure de la représentation graphique de la courbe sera : |
|
|
|
|
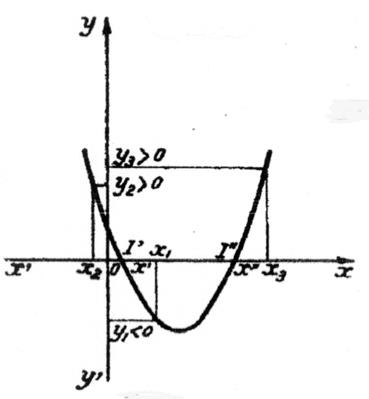
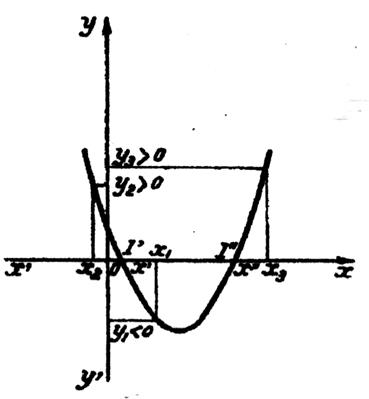
Si
b² - 4 ac
est positif et si « a >
0 », On remarque que : ► x2 <
x’ ; y2 > 0 , c’est à dire du signe de
« a » ► x3 >
x’’ ; y3 > 0 , c’est à dire du signe de « a » ► x’ < x 1
< x’’ ; y1 < 0 ; c’est à dire du signe de
« -a » |
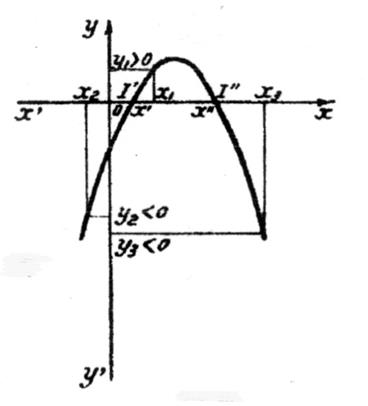
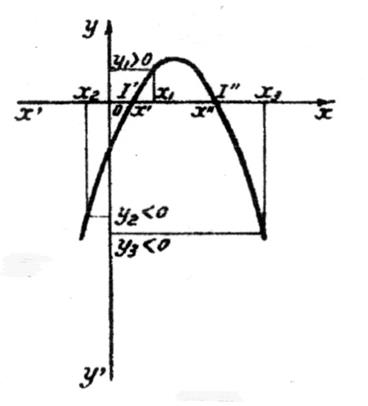
Si
b² - 4 ac
est positif et si « a < 0 », On remarque que : ► x2 <
x’ ; y2 <
0 ,
c’est à dire du signe de « a » ► x3 >
x’’ ; y3 < 0 , c’est à dire du signe de
« a » ► x’ < x 1
< x’’ ; y1 > 0 ; c’est à dire du signe de
« -a » |
|
Donc : les
points « I ‘ » et « I’’ » sont les points d’intersections de la
parabole avec l’axe des « x » ; « x’ » et
« x’’ » sont leurs abscisses respectives. 1-
l’ordonnée « y » correspondant à une abscisse « x »
inférieure à « x’ » ou supérieure à « x’’ » est du signe
de « a ». 2-
l’ordonnée « y » correspondant à une abscisse
« x » comprise entre
« x’ » et « x’’ » est du signe de « -a ». 3-
les intersections « I ‘ »
et « I’’ » ont des
ordonnées nulles. On en tire la règle
suivante : Si le discriminant est
positif le trinôme « y = a x² + b x + c » a le signe de « a » pour les
valeurs de « x » supérieures à la plus grande ou inférieures à la
plus petite des solutions de l’équation : « a x ² + b x + c =
0 ». Il a le signe contraire
de « a » pour les valeurs de « x » comprises entre ces
deux valeurs. Il est nul pour « x
= x’ » et « x = x’’ ». |
|
Résumé des trois règles :
On peut résumer ces trois
règles en un seul énoncé :
Le trinôme du second
degré de la forme « a x² + b x + c » a le signe de « a »
pour toute valeur de « x » sauf dans le cas où le discriminant étant
positif ou nul l’équation :
« a x² + b x + c =
0 » admet deux solutions distinctes ou égales « x’ » et
« x’’ » . Dans ce cas pour toute valeur de « x » comprise
entre « x’ » et x’’ » le trinôme a le signe contraire de « a »
. Pour toute valeur de
« x » égale à « x’ » et « x’’ » le trinôme est
nul.
Remarque : les règles précédentes
sont applicables aux binômes du second degré « a x² + b x » et « a x² + c » .
Ces binômes ne sont en effet que des trinômes incomplets dans lesquels les coefficient « c » et « b » sont
nuls.
A partir des
représentation graphiques suivantes , et pour chaque
cas :
1°) dire si « a » est
« positif » ou « négatif » .
2°) Dire si le
discriminant est « positif » « négatif » ou
« nul » .
|
N°1 : Le discriminant
est : …………………… La valeur de
« a » est : ……………. |
N°2 : Le discriminant est : …………………… La valeur de « a » est : ……………. |
|
|
|
|
N°3 Le discriminant est : …………………… La valeur de « a » est :
……………. |
N°4 Le discriminant est : …………………… La valeur de « a » est :
……………. |
|
|
|
|
N°5 Le discriminant est : …………………… La valeur de « a » est :
……………. |
N°6 Le discriminant est : …………………… La valeur de « a » est :
……………. |
|
|
|
