LOGICIEL warmaths Pour Aide et Formation Individualisée

PAGE D ‘ENTREE

Programme BAC PRO

INFORMATIONS PEDAGOGIQUES :

DOSSIER N° le second degré

Matière : MATHS.

TITRE : L E SECOND DEGRE

Classe : sortie de collége. NIVEAU :

OBJECTIFS : - Savoir étudier le signe d’un polynôme du second degré.

I ) Pré requis: (pour remédiation ou mise à niveau)

i9

Calcul avec des nombre décimaux

:i

i9

Tracer des équations du second degré.

:i

II ) ENVIRONNEMENT du dossier :

Index

Dossier précédent :

Dossier suivant :

Info :

III ) INFORMATIONS «  formation leçon » :

Test

COURS

Travaux auto - formation.

Corrigé des travaux auto - formation.

Contrôle

évaluation

INTERDISCIPLINARITE

Corrigé Contrôle

Corrigé évaluation

Chapitres :

Cours complémentaires :

i9

1. Définition : les équations et polynômes du second degré.

:i

i9

2. Résolution d’une équation du second degré.

:i

i9

3. Factorisation du polynôme du second degré.

:i

i9

4. Etude du signe : (par le calcul)

:i

5. Exercices d’application

IV ) DEVOIRS ( écrits):

Devoir diagnostique L tests.

Ÿ

Devoir Auto - formatif (intégré au cours)

Ÿ

Devoir Formatif « Contrôle : savoir » ; (remédiation)

Ÿ

Devoir Formatif «  Evaluation  savoir faire » (remédiation)

Ÿ

Devoir sommatif.

Contrôle et évaluation

Devoir certificatif : (remédiation)

Ÿ

* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .

Leçon	Titre
N°	L E SECOND DEGRE

	COURS
Corrigé des exercices du cours.		Devoir :

LES EQUATIONS ET POLYNOMES DU SECOND DEGRE

1°) Définition :

Une équation du second degré est une équation de la forme :

a x²+bx+c = 0 avec a,b,c nombre réels.

Exemple : 2x² -3x + 2 = 0.

2°) RESOLUTION D'UNE EQUATION DU SECOND DEGRE

Résoudre une équation du second degré consiste à trouver les valeurs de x(on les appelle les solutions ou racines de l'équation) qui vérifient l'équation : qx²+bx+c = 0 où a ¹ 0.

Vous admettrez la démarche suivante pour effectuer la résolution de cette équation :

1^ere étape : On calcule D = b²-4ac (D qui se lit "delta" est appelé le discriminant)

2^emeétape :

¶ Si D < 0 alors l'équation n'a pas de solutions

· Si D > 0 alors l'équation admet deux solution x₁ et x₂ qui se calculent à l'aide des formules :

¸ Si D = 0 alors l'équation admet une solution x₁. x₁ se calcule à l'aide de la formule :

Exemple On veut résoudre l'équation 2x² - 5x -3 = 0

1^ere étape : Dans ce cas : a = 2 ; b = -5 et c = -3

On calcule D = b²-4ac = 5² - 4´2´(-3) = 25 + 24 = 49

2^emeétape : D > 0 on calcule donc les deux solutions x₁ et x₂ :

Vérification : Pour vérifier les calculs il suffit de remplacer x par les valeurs de x₁ puis x₂ :

2 ´ 3² - 5 ´ 3 -3 = 18 - 15 - 3 = 0 donc 3 est bien une solution de l'équation 2x² - 5x -3 = 0

2 ´ (-1/2)² - 5 ´ (-1/2) -3 = 2/4 + 5/2 -3 = 0 donc -1/2 est bien une solution de l'équation 2x² - 5x -3 = 0

+Exercice n°1

Donner les solutions exactes puis arrondies à 0,1 près lorsque cela est possible des équations suivantes :

a) 3 x²+2 x – 1 = 0 b) 16 x² +40 x +25 = 0 c) -2x + x -1 = 0 d) .2 x² + 3 x -4 = 0

e) x²-2 x = 5 f) 2 x² = 3 x - 2 g) – 3 x² = 2- x h) 2 x² = 3 x² - 8 x + 3

3°) FACTORISATION D'UN POLYNOME DU SECOND DEGRE

La factorisation d'un polynôme du second degré de la forme ax²+ bx + c dépend du nombre de solutions de l'équation du second degré ax² +bx + c = 0 :

Si D > 0 alors l'équation admet deux solution x₁ et x₂ et le polynôme se factorise de la manière suivante :

Si D = 0 alors l'équation admet une solution x₁ et le polynôme se factorise de la manière suivante :

Si D < 0 alors l'équation n'a pas de solutions et le polynôme ne peut pas se factoriser.

+Exercice n°2

Pour les équations de l'exercice n°1, donner la factorisation de chaque polynôme lorsque cela est possible.

Application de la factorisation

On utilise la factorisation du polynôme du second degré afin d'étudier son signe. Faisons cette étude à l'aide d'un exemple :

Soit le polynôme 4x² - 7x - 2.

¶ Résoudre l'équation : 4x² - 7x - 2=0

· Factoriser le polynôme 4x² - 7x - 2.

¸ Résoudre les inéquations x + 0,25 > 0 et x - 2 > 0

¹ Reproduire et, en utilisant les résultats précédents, compléter le tableau suivant :

x	-0,25 2
Signe de x + 0,25	0
Signe de x - 2	0
Signe de 4x² - 7x - 2	0 0
4°) Etude du signe.

Généralisation :

¶ Si le polynôme n'a pas de solutions, alors pour tout réel x, le polynôme est du signe de a

· Si le polynôme a une ou deux solutions, alors on effectue la factorisation du polynôme et on construit un tableau de signe.

+Exercice n°3

On considère le polynôme P(x) = 16x² + 40x + 25.

¶ Résoudre l'équation 16x² + 40x +25 = 0

· En déduire une factorisation du polynôme P(x), puis le signe de P(x).

5°) EXERCICES D' APPLICATION

1°) Pour chacune des équations suivantes :

v Indiquer les valeurs de a, b et c et calculer le discriminant.

v En déduire le nombre de solutions de l'équation

X² + 9 x + 19 = 0 x² - 4 x + 4 = 0 -3 x² + x - 2 = 0 4 x² + 5 x - 6 = 0

2°) Résoudre les équations proposées :

x² + x - 6 = 0 x² - 6 x + 9 = 0 4 x² - 5 x - 6 = 0 x² - x + 1 = 0

9 x² + 6 x + 2 = 0 -2 x² - 13 x + 7 = 0 4 x² + 12 x + 9 =0 12 x² = 5 x +2

3°) Factoriser quand cela est possible les polynômes suivants :

x²+2 x -3 4 x ²+5 x- 6 - 2x²+5 x - 3 3 x²+2 x +2

4°) Pour chaque polynôme proposé :

Donner la factorisation

Etudier à l'aide d'un tableau de signe le signe du polynôme.

4 x² + 3 x - 1 3 x² - 4x + 4/3 x² - 3 x + 2 -2 x² + 3 x - 2

5°) Résoudre les inéquations suivantes : 15 x² - 17 x - 4 < 0 et 9 x² - 12 x + 4 ³ 0

6°) La courbe C est la courbe représentative de la fonction f définie sur l'ensemble des réels par

f(x) = -x² + 3 x

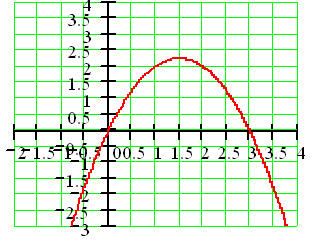
a) Résoudre graphiquement l'équation -x² + 3 x = 0

b) En utilisant le graphique indiquer le nombre de solutions des équations f (x) = 1 f(x) = 2,25 f(x) = 4

c) En utilisant les formules de résolution, résoudre les équations :

-x² + 3 x = 4 -x² + 3 x = 2,25 -x² + 3 x = 1

NB : on donnera les valeurs exactes des solutions puis les valeurs arrondies au centième.

Leçon	Titre
N°	TRAVAUX d ’ AUTO - FORMATION sur S

A venir TRAVAUX N° d ’ AUTO - FORMATION : CONTROLE

TRAVAUX N° d ‘ AUTO - FORMATION EVALUATION