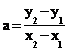|
|
FONCTIONS NUMERIQUES
I.
GENERALITES
Le
langage courant utilise souvent le terme "fonction :
"Le prix du plein de carburant
est fonction de la quantité versée"
"La pression atmosphérique est
fonction de l'altitude"
Dans
ces expressions, on veut indiquer qu'une grandeur dépend d'une autre. En
mathématiques, l'outil "fonction" sert également à exprimer une telle
dépendance mais également comment les deux grandeurs varient.
I.1. DEFINITION
Soit
I une intervalle de l'ensemble des nombres réels(Ensemble noté R), une fonction
numérique est une relation qui associe à tout élément x de I, un nombre réel
f(x) au plus.
On
note ¦ : I®R
x ® f(x)
x est la variable et ¦(x) est l'image de x. on
note y=¦(x)
L'ensemble des éléments de
I ayant une image est appelé ensemble de définition de ¦.
I.2. REPRESENTATION GRAPHIQUE D'UNE FONCTION
La
représentation graphique d'une fonction f dans un repère orthonormé( ce qui
signifie : même unité graphique sur les deux axes et axes perpendiculaires) ,
est l'ensemble des points de coordonnées (x ; f(x)).
On
dit que y=¦(x)
est une équation cartésienne de¦.
I.3. SENS DE VARIATION D'UNE FONCTION
Si
pour tous nombres x1 et x2 d'un intervalle I=[a ; b] tels
que x1 <x2 on a :
v
¦(x1) < ¦(x2) alors la
fonction est croissante sur I
v
¦(x1) > ¦(x2) alors la
fonction est décroissante sur I
v
¦(x1) = ¦(x2) alors la
fonction est constante sur I
Tableau
de variation : Une
flèche indique le sens de variation de ¦ sur [a;b]
|
|
Cas
d'une fonction ¦ croissante sur [a ; b] |
|
|
x |
a b |
|||
|
¦ |
|
+Exercice n°1
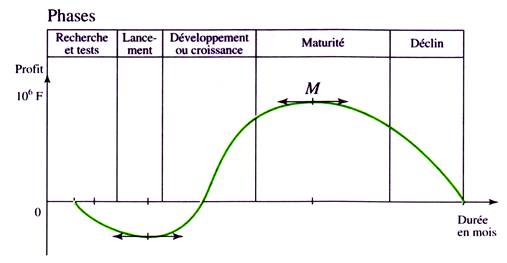
La
représentation graphique ci-dessous, permet d'analyser le profit durant les
phases constituant le cycle de vie d'un produit.
Unités
des axes : en abscisses :
En ordonnée :
1°)
Recopier et compléter le tableau de variations ci dessous

2°)
Déterminer graphiquement : a) la durée nécessaire pour atteindre un profit
maximal
b)
Le profit maximal M
c)
La durée de vie du produit.
3°)
Que se passe t-il : lors des 30 premiers mois ? au bout de 82 mois ?
 +Exercice n°2
+Exercice n°2
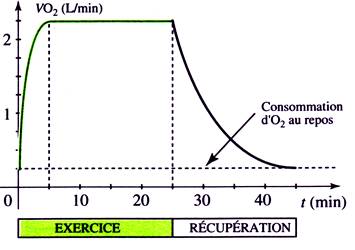
La
courbe c-dessous représente la consommation en oxygène (VO2) au
cours d'un exercice sportif et de la période de récupération qui le suit.
Donner
le tableau de variation de VO2 (en L/min) en fonction du temps t (en
min).
II.
LES FONCTIONS USUELLES
II.1. FONCTIONS
AFFINES
Définition : On appelle fonction affine toute fonction
définie par une expression de la forme : ¦(x) = ax + b avec a et b
nombres réels
Représentations
graphiques
Dans
un repère orthonormé, la représentation graphique est une droite d'équation y =
ax + b, a est le coefficient directeur de la droite et b l'ordonnée à
l'origine.
Exemple soit ¦(x) = 2x + 3, comme la
représentation graphique est une droite, il suffit d'avoir les coordonnées de
deux points pour pouvoir la tracer. On calcule donc les coordonnées de deux
points.
Pour
x = 0 on a ¦(0)
= 2 ´
0 + 3 = 3, la droite passera donc par le point A(0;3)
Pour
x = 1 on a ¦(1)=
2 ´
1 + 3 = 2 + 3 = 5, la droite passera par le point B( 1 ; 5)
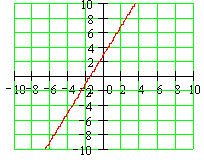
La représentation
graphique est donc ( j'ai choisi l'intervalle [-10;10] pour cet exemple) :